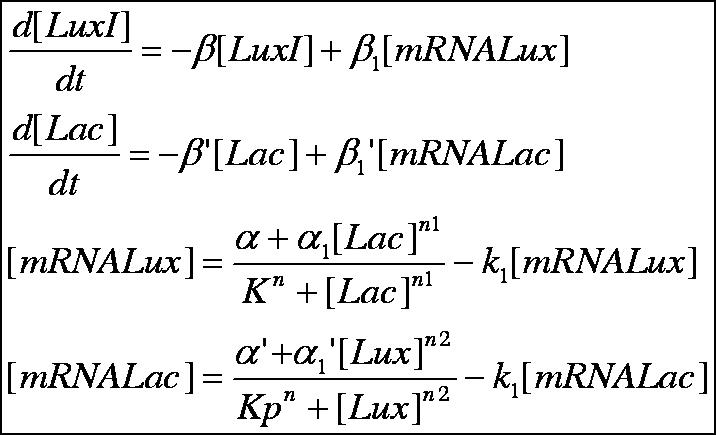From 2007.igem.org

A major part of the team this year was the theory team who were developing artificial simulations in mathematica xlr8r to outline possible oscillatory systems.

Currently, our simulations are based on a deterministic approach, which mean that the direction of a reaction is fixed; which, is not perfectly correct as diffusion particles tend to migrate in a stoichiometric manner. Nevertheless, by altering parameters involved with transcription, translation, diffusion coefficients, coupling constants and rate equations we were able to model a perfect oscillatory system which we are attempting to simulate in the lab.

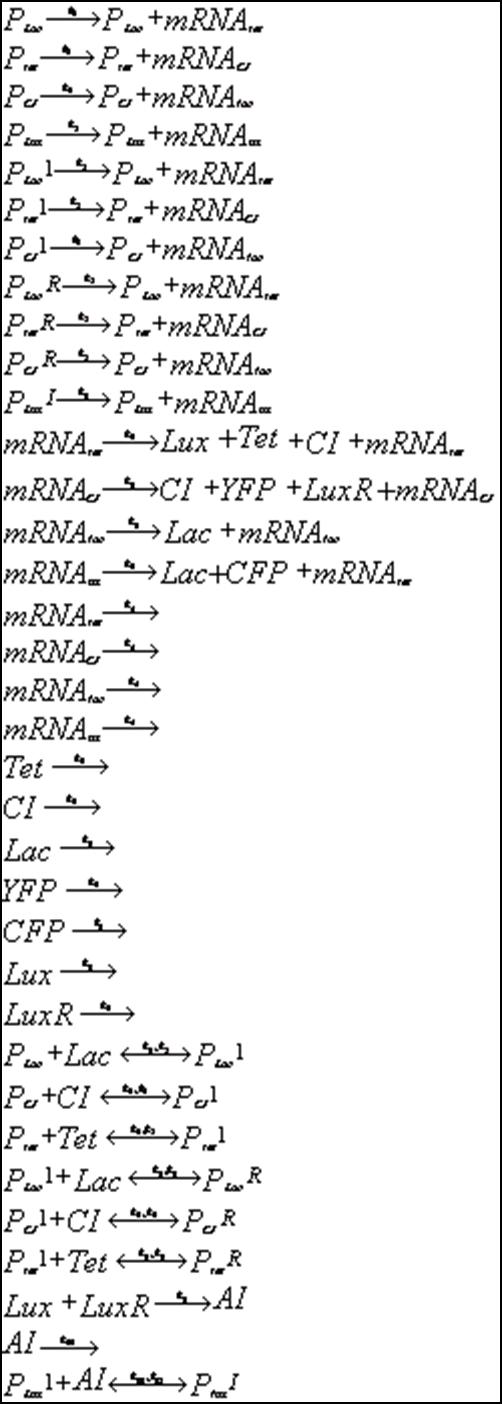
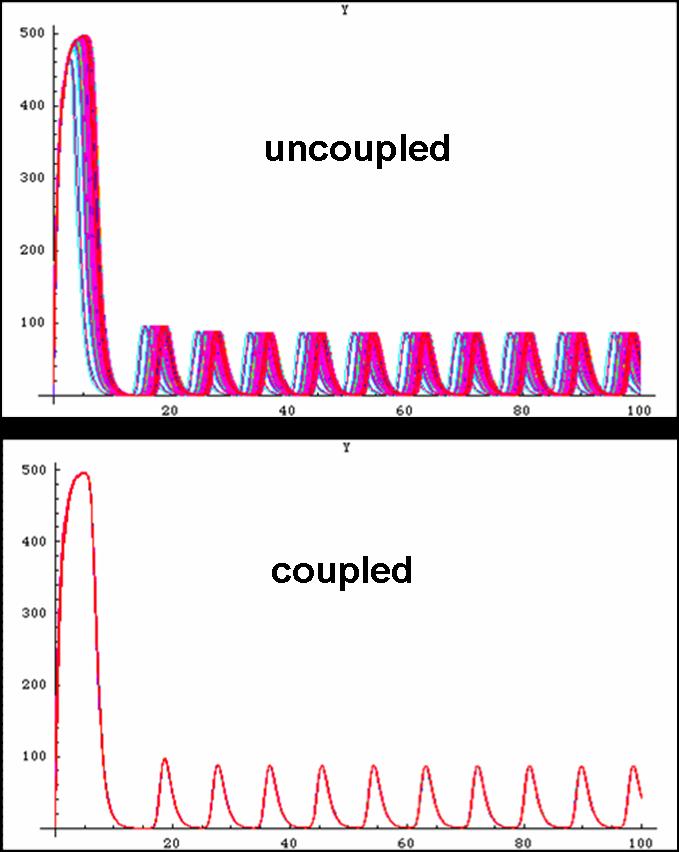
Below is outlined the series of deterministic rate constants that were used in the formation of the system. As mentioned, the coefficients were altered to find systems that were both in phase, and out of phase as can be seen in the diagrams.

Discrete Rate Equations:

---

First, the system is initially put in a random configuration such that the cells are not oscillating in phase. Then, within two periods, the cells acquire the proper in phase oscillations. In addition, the oscillatory period is 20 minutes as dictated in the simulations which, is precisely what was demonstrated in the lab thus outlining the tremendous potential for the biological system to replicate the simulated system.

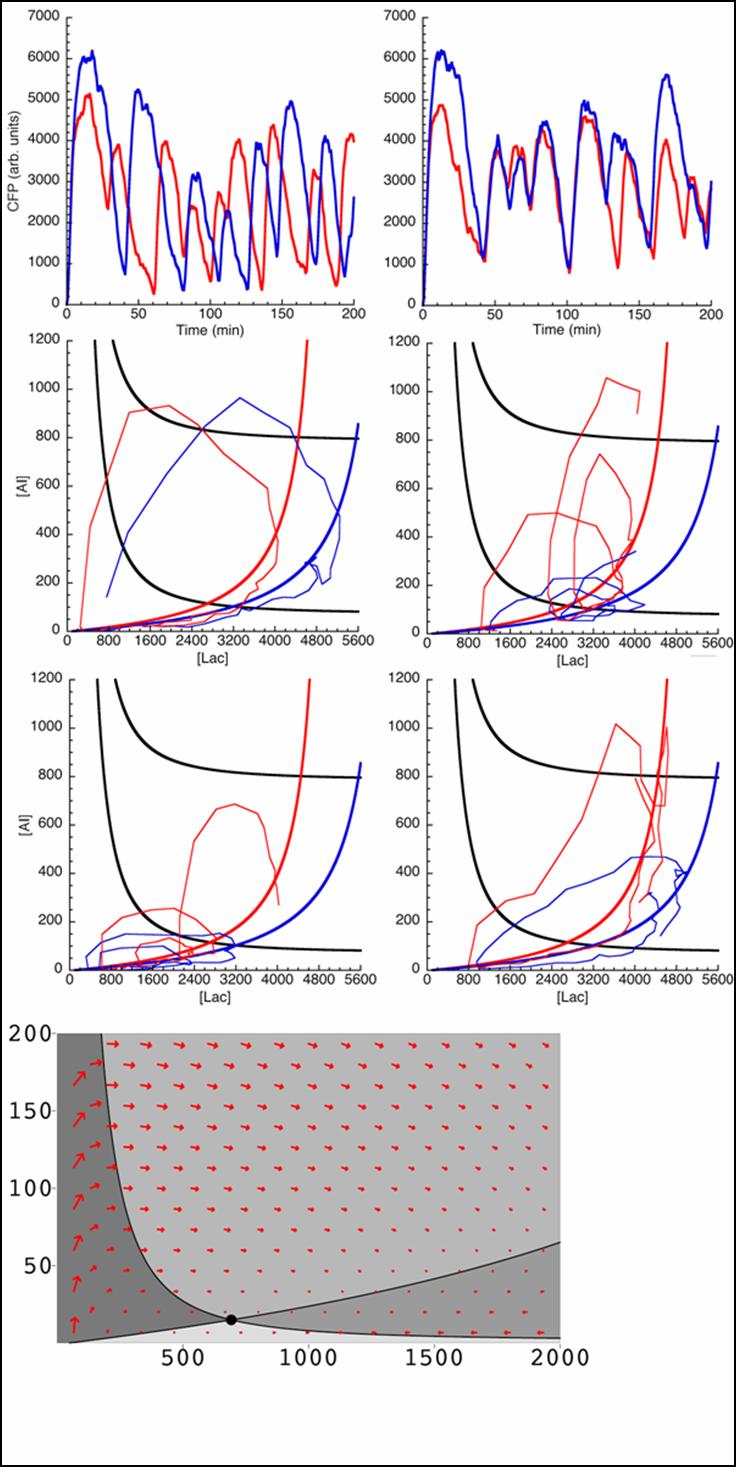
Unfortunately, some compensations had to be made to the system to make it work. First, the cells are not actually circular though randomly fixed to a grid-system thus making the abnormal cell shapes. Additionally, the system was modelled as one mother cell instead of many interacting cells, that simply emits and reabsorbs the autoinducer many times. When a network is produced, the cells are modelled as touching one another thus there is no membrane passage nor diffusion through a medium to be considered. In light of this, oscillations were still produced thus making the potential of a functional oscillating system.

---

Other considerations:

Further, we are currently working on implementing the Gillespie algorithm to solve the problem of the inaccuracies of the deterministic approach.

The Gillespie algorithm will make it possible to simulate the proper diffusion of the AI based on the fact that at every grid point, a new ‘reaction’ occurs where the AI molecule can make an independent decision on to which adjacent cell that the particle can diffuse to.

The problem with this approach is to obtain solutions we require long, memory-intensive hardware which means a new parallel computer system to implement such algorithms.
Still, many tweaks are being worked out with the simulations including, as alluded to earlier, the problem with the diffusion of the AI across the membrane and the rate equations for the membrane proteins, the three-dimensional diffusion of the AI in all space, the circular nature of cells, implementing the system on a large number of cells rather than a small subset and the formulation of accurate rate equations with the proper rate constants.