Traveling Salesperson Problem?
From 2007.igem.org
Wideloache (Talk | contribs) |
Wideloache (Talk | contribs) |
||
| Line 2: | Line 2: | ||
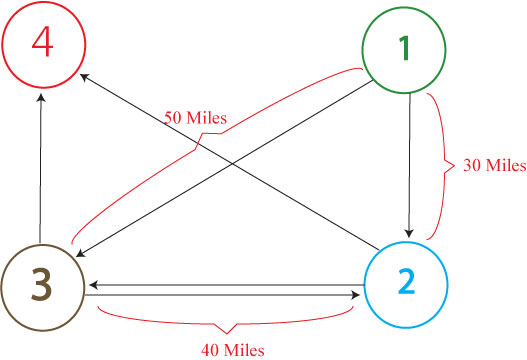
This graph above shows a modified complete graph with edges leaving the ending node (#4), returning to the start node (#1), and moving from the start to the stop node removed. If we wanted to solve this weighted and directed graph for the shortest path through all nodes, starting at node #1, ending at node #4, and passing through each node only once, we could use our current HPP ''E. coli'' computer construct with one slight modification. | This graph above shows a modified complete graph with edges leaving the ending node (#4), returning to the start node (#1), and moving from the start to the stop node removed. If we wanted to solve this weighted and directed graph for the shortest path through all nodes, starting at node #1, ending at node #4, and passing through each node only once, we could use our current HPP ''E. coli'' computer construct with one slight modification. | ||
| - | + | <br> | |
[[Image:TSP 4N shortest.jpg|900px]] | [[Image:TSP 4N shortest.jpg|900px]] | ||
Instead of putting each half-gene back to back along an edge, we could add in spacers of specified lengths that would allow us to model the various weights in the graph above. These weights would give edges different lengths (in base pairs). After performing PCR on all of the solved plasmids (with primers binding to the promoter and terminator), we would be able to find the shortest path through all of the nodes by running the PCR products on a gel. Because the total length of the genes in any Hamiltonian Path through the graph is a constant, the smallest solved fragment will have the lowest total spacer length and will, therefore, be the solution to the Traveling Salesperson Problem (shown above). | Instead of putting each half-gene back to back along an edge, we could add in spacers of specified lengths that would allow us to model the various weights in the graph above. These weights would give edges different lengths (in base pairs). After performing PCR on all of the solved plasmids (with primers binding to the promoter and terminator), we would be able to find the shortest path through all of the nodes by running the PCR products on a gel. Because the total length of the genes in any Hamiltonian Path through the graph is a constant, the smallest solved fragment will have the lowest total spacer length and will, therefore, be the solution to the Traveling Salesperson Problem (shown above). | ||
| - | + | <br> | |
[[Image:TSP 4N longer.jpg|900px]] | [[Image:TSP 4N longer.jpg|900px]] | ||
| - | This image shows an alternate route through the graph. The length of this fragment is longer than the length of the solution. | + | This image shows an alternate route through the graph. The length of this fragment is longer than the length of the solution to the TSP. |
| - | + | <br> | |
[[Image:TSP 4N falsepos.jpg|900px]] | [[Image:TSP 4N falsepos.jpg|900px]] | ||
False positives can also come into play with this construct. However, if the graph satisfies geometric constraints (i.e. all edges in the graph obey the rules for triangles) then any false positive will be longer than any Hamiltonian path through the graph. If the graph does not satisfy geometric constraints, then certain rules must be put into place when choosing spacer length to avoid having flase positive PCR products that are longer than the real solution. | False positives can also come into play with this construct. However, if the graph satisfies geometric constraints (i.e. all edges in the graph obey the rules for triangles) then any false positive will be longer than any Hamiltonian path through the graph. If the graph does not satisfy geometric constraints, then certain rules must be put into place when choosing spacer length to avoid having flase positive PCR products that are longer than the real solution. | ||
Revision as of 01:22, 29 June 2007
This graph above shows a modified complete graph with edges leaving the ending node (#4), returning to the start node (#1), and moving from the start to the stop node removed. If we wanted to solve this weighted and directed graph for the shortest path through all nodes, starting at node #1, ending at node #4, and passing through each node only once, we could use our current HPP E. coli computer construct with one slight modification.

Instead of putting each half-gene back to back along an edge, we could add in spacers of specified lengths that would allow us to model the various weights in the graph above. These weights would give edges different lengths (in base pairs). After performing PCR on all of the solved plasmids (with primers binding to the promoter and terminator), we would be able to find the shortest path through all of the nodes by running the PCR products on a gel. Because the total length of the genes in any Hamiltonian Path through the graph is a constant, the smallest solved fragment will have the lowest total spacer length and will, therefore, be the solution to the Traveling Salesperson Problem (shown above).
![]()
This image shows an alternate route through the graph. The length of this fragment is longer than the length of the solution to the TSP.

False positives can also come into play with this construct. However, if the graph satisfies geometric constraints (i.e. all edges in the graph obey the rules for triangles) then any false positive will be longer than any Hamiltonian path through the graph. If the graph does not satisfy geometric constraints, then certain rules must be put into place when choosing spacer length to avoid having flase positive PCR products that are longer than the real solution.