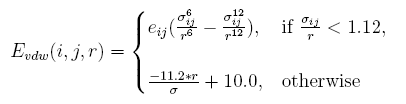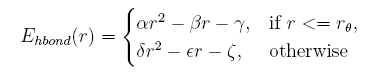USTC/Repressor Evolution in Silico
From 2007.igem.org
Contents |
Introduction
Protein Design
Designing efficient proteins for a broad of different processes is of tremendous practical fun both in science and industry. [1]. Computational design is well concerned for its efficiency and convenience. Redesigning the protein-DNA complexes is so important that it is the first step concerned at the beginning of redesigning the active sites. Milestones have been reported[2-5]. Here we are trying to construct several artificial repressor-operator pairs to serve as the connecting wires of our system.
There are several steps in protein design[6]. Firstly, generate a random structure with random sequence. Secondly, optimize the structure of the side-chains for each random sequence. Thirdly, give each random sequence a score and select the sequence with the best score. In almost all the conditions, sequence candidates is countless. There will be 2020 candidates if we redesign 20 positions. Therefore, great efforts have been made to reduce the computation complexity[1,7-14], for example, using a rotamer library that is composed of several discrete conformation to represent the status of sidechains, employing pair-wise energy function to score sequences, searching with Monte Carlo, Genetic Algorithm and etc. Another key here is the score function. It functions to give higher scores to sequences performs better in experiments. Up till now, no efficient method in silico has been given to examine the computational design results. One way to examine them is to express the sequences designed in practical experiments.
Lac Repressor
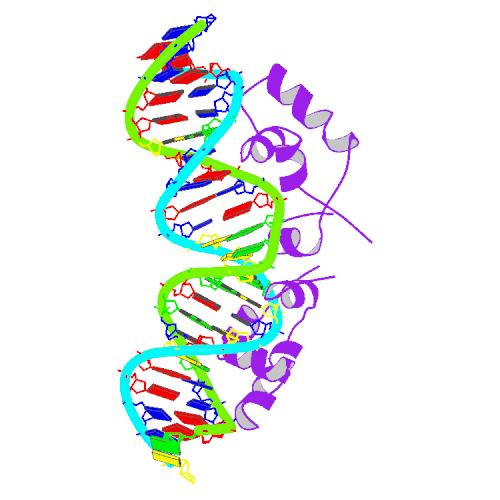
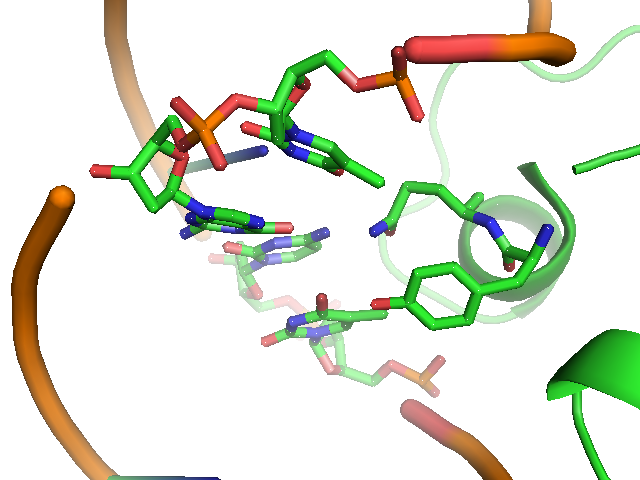
The lac repressor is a DNA-binding protein which inhibits the expression of genes coding for proteins involved in the metabolism of lactose in bacteria[15]. There are three distinct regions in the protein. The headpiece, a fragment contains approximately 51 amino acids from its N-terminal together with a helix-turn-helix motif, is the only region that serves to bind DNA. Figure 1 shows the NMR structure of the complex with two headpieces of the lac repressor and its nature operator[16]. A series of experiments have shown that the mutation on the 7th, 9th site of the operator can sharply reduce the stability of the complex[15-17]. Figure 2 shows the structure of DNA sequence on site 7,8,9 and the residues related to them. From this structure, we come to know that Residue 17 and 18, which are YQ in native repressor sequence, take charge in recognizing the specific DNA sequence. The binding specificity may be adapted by changing the two positions.
As to the wires exempt from interference, the binding specificity is highly required for the repressor-operator pairs. It is reported that the mutated repressor with VA at Position 17,18 can bind to the transitionally mutated operator on Site 7 [18]. Transversion might lead to changes too big for us to rebuild the DNA structure according to the native structure, thus, no mutated lac repressor can bind to it. Therefore, only transition mutation made on the DNA, and the structure was built manually according to native structure and then optimized with gromos96, 43a1 forcefield. In this way, we have obtained four DNA structures. Furthermore, we aims at accomplish in the near future redesigning the recognition region of the repressor for specific bindings to the operator DNA.
Computational Model
Score function
Our score function here is a combination of physic-based potentials and knowledge-based potentials. The energy items should be modified to suit the rotamer library. The modified van der waal interaction, hydrogen bond energy, solvent accessible surface area (SASA) and electrostatic interaction are applied as items for the score function.
Linearize van der waal interaction
The vdw interaction energy[19] between atom i and atom j at the distance of r is:
Clashes in redesigned structures more often occur than those in native structures. Obviously, it is because that side chains of the proteins are represented in a discrete form in artificial structures. A tolerate acception of clash is given by linearizing the replusive item , and the parameters are determined by taking tests.
Hydrogen bond energy
The distance between the donor and the acceptor given, the hydrogen bond energy is:
When side chain structures are described in the form of rotamers, the distance between the donor and acceptor changes as well. Moreover, the position of hydrogen atom cannot be obtained in a easy way because of its rotation. Here we give a knowledge-based potential depend on the distance of donor and acceptor in the coarse-grained structures.
SASA and Electrostatic Interaction
The energy items for SASA and electostatic interaction are defined by TM Handel and her co-workers[8].
Parameterization
We work with different score functions to respectively optimize the side chains of the proteins and to select sequences. It is because that they are totally different in nature. Optimization of side-chains tells the three-dimensional structure of the complex after the amino acids there are changed, and the sequence selection of amino acids shows the more suitable sequence for binding. The role of the two energy items in the two processes are not the same. The parameters for the optimized side chain are obtained by training with 49 structures picked from PDBbind library [20], and those for sequence selection are gained by training with the results of directed evolution.
Results
In this particular problem, only 2 positions in the protein were to be changed. Therefore, there are only 400 candidates. The computational complexity is no longer a problem here. We have optimized the side chains of each candidate, and have worked out the each energy item. With the help of directed evolution, we have found the suitable parameters for sequence selection. Additionally, we predict that some other chains may also work in this situation. Testing experiments have already been in process at the same time.
References
- Zanghellini, A.; Jiang, L.; Wollacott, A. M.; Cheng, G.; Meiler, J.; Althoff, E. A.; Röthlisberger, D. & Baker, D. (2006), 'New algorithms and an in silico benchmark for computational enzyme design.', Protein Sci 15(12), 2785--2794.
- Dahiyat, B. I. & Mayo, S. L. (1997), 'De novo protein design: fully automated sequence selection.', Science 278(5335), 82--87.
- Kuhlman, B.; Dantas, G.; Ireton, G. C.; Varani, G.; Stoddard, B. L. & Baker, D. (2003), 'Design of a novel globular protein fold with atomic-level accuracy.', Science 302(5649), 1364--1368.
- Looger, L. L.; Dwyer, M. A.; Smith, J. J. & Hellinga, H. W. (2003), 'Computational design of receptor and sensor proteins with novel functions.', Nature 423(6936), 185--190.
- Ashworth, J.; Havranek, J. J.; Duarte, C. M.; Sussman, D.; Monnat, R. J.; Stoddard, B. L. & Baker, D. (2006), 'Computational redesign of endonuclease DNA binding and cleavage specificity.', Nature 441(7093), 656--659.
- Lippow, S. M. & Tidor, B. (2007), 'Progress in computational protein design.', Curr Opin Biotechnol 18(4), 305--311.
- Georgiev, I.; Lilien, R. H. & Donald, B. R. (2006), 'Improved Pruning algorithms and Divide-and-Conquer strategies for Dead-End Elimination, with application to protein design', Bioinformatics 22, e174-83.
- Pokala, N. & Handel, T. M. (2004), 'Energy functions for protein design I: efficient and accurate continuum electrostatics and solvation.', Protein Sci 13(4), 925--936.
- Gordon, D. B.; Hom, G. K.; Mayo, S. L. & Pierce, N. A. (2003), 'Exact rotamer optimization for protein design', Journal of Computational Chemistry 24, 232-43.
- Holm, L. & Sander, C. (1992), 'Fast and simple Monte Carlo algorithm for side chain optimization in proteins: application to model building by homology', Proteins 14, 213-23.
- Lilien, R. H.; Stevens, B. W.; Anderson, A. C. & Donald, B. R. (2005), 'A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase a phenylalanine adenylation enzyme.', J Comput Biol 12(6), 740--761.
- Pokala, N. & Handel, T. M. (2005), 'Energy functions for protein design: adjustment with protein-protein complex affinities, models for the unfolded state, and negative design of solubility and specificity.', J Mol Biol 347(1), 203--227.
- Shah, P. S.; Hom, G. K. & Mayo, S. L. (2004), 'Preprocessing of rotamers for protein design calculations', Journal of Computational Chemistry 25, 1797-800.
- Street, A. G. & Mayo, S. L. (1998), 'Pairwise calculation of protein solvent-accessible surface areas.', Fold Des 3(4), 253--258.
- Lewis, M.; Chang, G.; Horton, N. C.; Kercher, M. A.; Pace, H. C.; Schumacher, M. A.; Brennan, R. G. & Lu, P. (1996), 'Crystal structure of the lactose operon repressor and its complexes with DNA and inducer.', Science 271(5253), 1247--1254.
- Lehming, N.; Sartorius, J.; Niemöller, M.; Genenger, G.; v Wilcken-Bergmann, B. & Müller-Hill, B. (1987), 'The interaction of the recognition helix of lac repressor with lac operator.', EMBO J 6(10), 3145--3153.
- Sartorius, J.; Lehming, N.; Kisters, B.; von Wilcken-Bergmann, B. & Müller-Hill, B. (1989), 'lac repressor mutants with double or triple exchanges in the recognition helix bind specifically to lac operator variants with multiple exchanges.', EMBO J 8(4), 1265--1270.
- Salinas, R. K.; Folkers, G. E.; Bonvin, A. M. J. J.; Das, D.; Boelens, R. & Kaptein, R. (2005), 'Altered specificity in DNA binding by the lac repressor: a mutant lac headpiece that mimics the gal repressor.', Chembiochem 6(9), 1628--1637.
- Grigoryan, G.; Ochoa, A. & Keating, A. E. (2007), 'Computing van der Waals energies in the context of the rotamer approximation.', Proteins 68(4), 863--878.
- Wang, R.; Fang, X.; Lu, Y. & Wang, S. (2004), 'The PDBbind database: collection of binding affinities for protein-ligand complexes with known three-dimensional structures.', J Med Chem 47(12), 2977--2980.