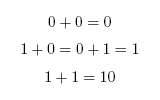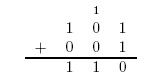Waterloo
From 2007.igem.org
| Line 13: | Line 13: | ||
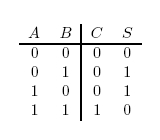
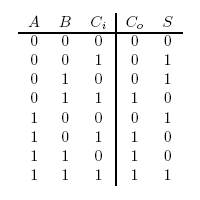
The value 10 in binary represents 2. The adder can be seen as having two outputs: a sum and a carry. The carry being the number that would be carried into the next column when adding by hand (Figure 1). For example, the sum of 101 + 001 is 110. The problem is in the second column. It needs to add the values in the second column and the carry from the first column (Figure 2). To fix this problem, we need a full adder. In addition to our inputs A and B, it will take a carry in Ci. The behavior of a full adder can be seen in figure 3. | The value 10 in binary represents 2. The adder can be seen as having two outputs: a sum and a carry. The carry being the number that would be carried into the next column when adding by hand (Figure 1). For example, the sum of 101 + 001 is 110. The problem is in the second column. It needs to add the values in the second column and the carry from the first column (Figure 2). To fix this problem, we need a full adder. In addition to our inputs A and B, it will take a carry in Ci. The behavior of a full adder can be seen in figure 3. | ||
| + | |||
''Figure 1: Half Adder Truth Table'' | ''Figure 1: Half Adder Truth Table'' | ||
| Line 27: | Line 28: | ||
Once we have a full adder, we can chain them to add any number of bits. This is called a ripple carry adder (Figure 4). However the project will not be a ripple carry adder. Only one full-adder unit will be produced. | Once we have a full adder, we can chain them to add any number of bits. This is called a ripple carry adder (Figure 4). However the project will not be a ripple carry adder. Only one full-adder unit will be produced. | ||
| + | |||
''Figure 4: Block Diagram of a Ripple Carry Adder'' | ''Figure 4: Block Diagram of a Ripple Carry Adder'' | ||
| - | + | ||
'''2. Implementation of the Adder''' | '''2. Implementation of the Adder''' | ||
| Line 36: | Line 38: | ||
The current design designates the three inputs A, B, and Ci as red light, tetracycline, and lactose respectively. Ideally, one of these (preferably lactose) will be replaced by blue light. The outputs Co and S will be expressed using red fluorescent and green | The current design designates the three inputs A, B, and Ci as red light, tetracycline, and lactose respectively. Ideally, one of these (preferably lactose) will be replaced by blue light. The outputs Co and S will be expressed using red fluorescent and green | ||
fluorescent protein. The development of the design (Figure 5) best explains how it functions. | fluorescent protein. The development of the design (Figure 5) best explains how it functions. | ||
| + | |||
''Figure 5: Project Gene Design'' | ''Figure 5: Project Gene Design'' | ||
Revision as of 00:54, 6 August 2007
 University of Waterloo iGEM Team
University of Waterloo iGEM Team Contents |
Our Team
The UW iGEM team is a very interdisciplinary group. Our team members span the four faculties of Science, Mathematics, Engineering, and Applied Health Sciences and include the programs of Biology, Health Studies, Computer Science, Bioinformatics, Computer Engineering, Electrical Engineering, Chemical Engineering, and Mathematical Physics at undergraduate and graduate levels. Even our professor advisors are cross-appointed to two other faculties. Our diverse backgrounds bring together a wide range of skills and ideas to the iGEM project. iGEM is giving us the opportunity to apply the skills learned in our lectures and labs to real life applications in molecular biology and biotechnology.
Our Design
1. A Biological Full Adder
Our project is a light and chemical controlled full adder meant to reproduce a circuit element called a full-adder within a biological system. In the electronic version, signals come in in binary as values of 0 or 1 which correspond to 0 V or 5 V respectively. For the biological version, we make 0 represent basal expression of a protein and 1 represent full expression of a protein. The 0 value does not to need to be 0 as much as there needs to be a noticeable difference between 0 and 1. A simple half-adder takes in two bits and adds them. The possibilities are as follows:
The value 10 in binary represents 2. The adder can be seen as having two outputs: a sum and a carry. The carry being the number that would be carried into the next column when adding by hand (Figure 1). For example, the sum of 101 + 001 is 110. The problem is in the second column. It needs to add the values in the second column and the carry from the first column (Figure 2). To fix this problem, we need a full adder. In addition to our inputs A and B, it will take a carry in Ci. The behavior of a full adder can be seen in figure 3.
Figure 1: Half Adder Truth Table
Figure 2: Long Addition of 101 + 001
Figure 3: Full Adder Truth Table
Once we have a full adder, we can chain them to add any number of bits. This is called a ripple carry adder (Figure 4). However the project will not be a ripple carry adder. Only one full-adder unit will be produced.
Figure 4: Block Diagram of a Ripple Carry Adder
2. Implementation of the Adder
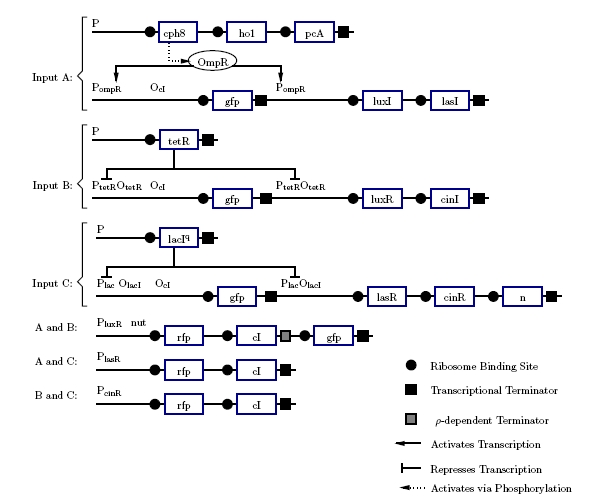
The current design designates the three inputs A, B, and Ci as red light, tetracycline, and lactose respectively. Ideally, one of these (preferably lactose) will be replaced by blue light. The outputs Co and S will be expressed using red fluorescent and green fluorescent protein. The development of the design (Figure 5) best explains how it functions.
Figure 5: Project Gene Design
If none of the promotors are active, nothing happens. This gives us 0 + 0 + 0 = 0 for free. The carry is on when at least two inputs are active. In digital logic, this is an AND gate. The quorum-sensing systems work much like AND gate. Only when both LuR and LuxI are present will anything under the control of Plux be expressed. To accomplish this, LuxI will be put under the control of A and LuxR under the control of B. Only if A and B are active will genes under Plux be transcribed. The three quorum-sensing system Lux, Las, and Cin, cover the combinations A and B, A and Ci, and, B and C. If we make any single input produce GFP, that will make S = 1 in the cases where 1 + 0 + 0, but this will be incorrect in the cases where 1 + 1 + 0. If the input is 1 + 1 + 0, the sum should be repressed. This can be done using the cI repressor. All of the AND gates will produce cI which will stop GFP production if two or more inputs are active. This will produce correct output in all but one case: 1 + 1 + 1. GFP will be repressed because all of the AND gates will be producing cI. To fix this, GFP will be added to the A and B gene after the terminator. Using ’s antitermination system under the control of Ci, GFP will be produced when A and B and Ci are active. This set of genes should match the output shown in figure 3.
3. Photo-Active Blue
CURRENTLY IN PROGRESS
The Inputs
We have chosen to use light as an input for the reasons that it does not require altering the media, it can be turned on and off rapidly, and it has extremely high resolution and accuracy. We will be using one light input in the form of red light and two chemical inputs. The red light will be detected by the previously used Cph1/EnvZ fusion protein ([http://partsregistry.org/Part:BBa_I15010 BBa_I15010]).
The chemical inputs to be used are currently being determined.
Supporters
We would like to thank:
[http://www.science.uwaterloo.ca Faculty of Science] — [http://www.math.uwaterloo.ca Faculty of Math] — [http://www.engineering.uwaterloo.ca Faculty of Engineering]
[http://www.weef.uwaterloo.ca Waterloo Engineering Endowment Fund] — [http://www.mef.uwaterloo.ca Mathematics Endowment Fund]