ETHZ/FlipFlop

From 2007.igem.org

(Difference between revisions)
(→'''.:: An Engineer's View on Biological Learning ::.''')
(→'''.:: An Engineer's View on Biological Learning ::.''')
Line 3: Line 3:
An equivalent system behavior can be realized using [http://en.wikipedia.org/wiki/Flip-flop_%28electronics%29 flip-flops], implemented by [http://en.wikipedia.org/wiki/Logic_gate logical gates]:
An equivalent system behavior can be realized using [http://en.wikipedia.org/wiki/Flip-flop_%28electronics%29 flip-flops], implemented by [http://en.wikipedia.org/wiki/Logic_gate logical gates]:
-
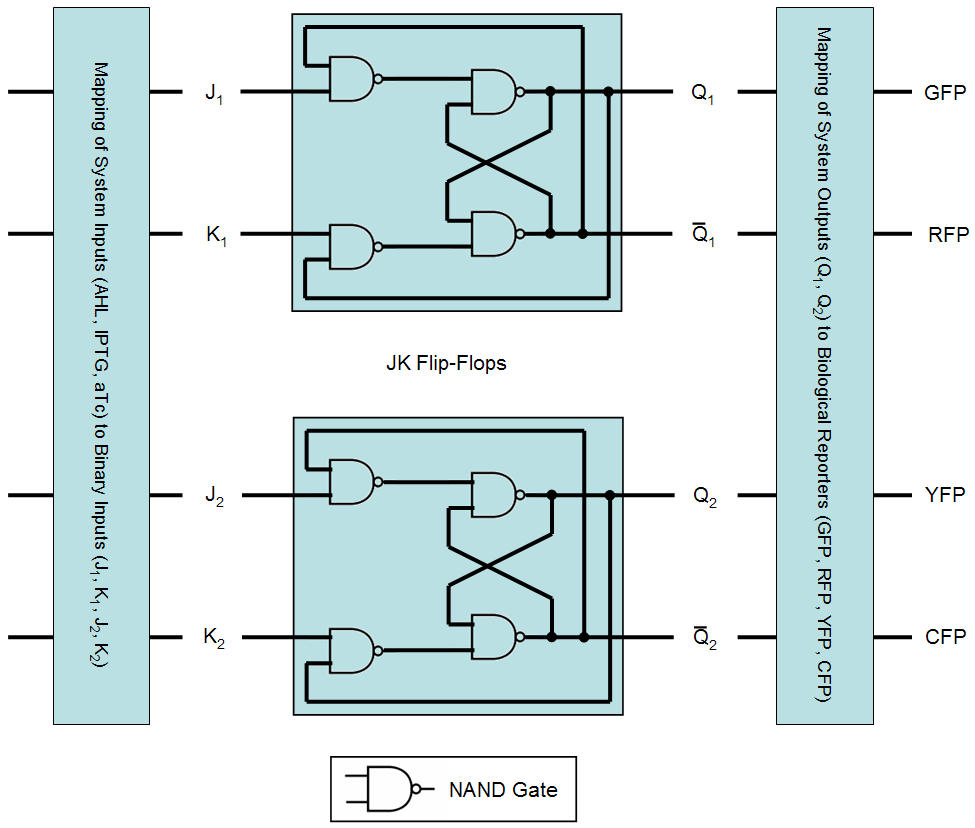
As already shown in the [https://2007.igem.org/ETHZ/FSM finite state machine representation], the proposed system consists of three different states and recognizes four different inputs. In total, this adds up to twelve different transitions. In order to implement these twelve transitions with a digital system, at least four binary inputs are required (allowing for a maximum of 16 transitions) and since the proposed system has four different outputs, at least two binary outputs are needed. Here, we chose an implementation using two JK flip-flops consisting of [http://en.wikipedia.org/wiki/Nand_gate#NAND_gate NAND gates]. An overview of the resulting system is given in Fig. 1 and details concerning flip-flop and NAND gate behavior are given in the following table:
+
As already shown in the [https://2007.igem.org/ETHZ/FSM finite state machine representation] (FSM), the proposed system consists of three different states and recognizes four different inputs. In total, this adds up to twelve different transitions. In order to implement these twelve transitions with a digital system, at least four binary inputs are required (allowing for a maximum of 16 transitions) and since the proposed system has four different outputs, at least two binary outputs are needed. Here, we chose an implementation using two JK flip-flops consisting of [http://en.wikipedia.org/wiki/Nand_gate#NAND_gate NAND gates]. An overview of the resulting system is given in Fig. 1 and details concerning flip-flop and NAND gate behavior are given in the following table:
{|  class="wikitable" border="1" cellspacing="0" cellpadding="2" style="text-align:left; margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;"
{|  class="wikitable" border="1" cellspacing="0" cellpadding="2" style="text-align:left; margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;"
Line 14: Line 14:
| 1 || 0 || 1                    || || 1 || 0 || 1
| 1 || 0 || 1                    || || 1 || 0 || 1
|- align="center"
|- align="center"
-
| 1 || 1 || ¬''Q''<sub>prev</sub> || || 1 || 1 || 0
+
| 1 || 1 || [http://en.wikipedia.org/wiki/Inverse_%28logic%29 ¬]''Q''<sub>prev</sub> || || 1 || 1 || 0
|}
|}
Line 39: Line 39:
|J<sub>1</sub>=1, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
|J<sub>1</sub>=1, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
|J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=1
|J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
|}
 +
 +
Here, we assume that the FSM system states ''q''<sub>0</sub>, ''q''<sub>1</sub>, ''q''<sub>2</sub> are mapped to the outputs ''Q''<sub>1</sub> and ''Q''<sub>2</sub> as follows:
 +
 +
{|  class="wikitable" border="1" cellspacing="0" cellpadding="2" style="text-align:left; margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;"
 +
!FSM states/output coding !! ''Q''<sub>1</sub> !! ''Q''<sub>2</sub>
 +
|- align="center"
 +
!J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=1, K<sub>2</sub>=0
 +
!J<sub>1</sub>=0, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
!J<sub>1</sub>=1, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
!J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
!J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=1, K<sub>2</sub>=0
 +
!J<sub>1</sub>=0, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
!J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=0
 +
!J<sub>1</sub>=0, K<sub>1</sub>=0, J<sub>2</sub>=1, K<sub>2</sub>=1
 +
!J<sub>1</sub>=1, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=0
 +
!J<sub>1</sub>=1, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=0
 +
!J<sub>1</sub>=1, K<sub>1</sub>=0, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
!J<sub>1</sub>=0, K<sub>1</sub>=1, J<sub>2</sub>=0, K<sub>2</sub>=1
 +
|- align="center"
 +
| ''green''
 +
| ''green''
 +
| ''red''
 +
| ''green''
 +
| ''green''
 +
| ''green''
 +
| ''yellow''
 +
| ''blue''
 +
| ''yellow''
 +
| ''yellow''
 +
| ''yellow''
 +
| ''yellow''
 +
|}
 +
 +
The final mapping from transitions to the biological reporters is then given by:
 +
{|  class="wikitable" border="1" cellspacing="0" cellpadding="2" style="text-align:left; margin: 1em 1em 1em 0; background: #f9f9f9; border: 1px #aaa solid; border-collapse: collapse;"
 +
!
 +
|- align="center"
 +
! ''Q''<sub>1</sub>
 +
|
 +
|- align="center"
 +
! ''Q''<sub>2</sub>
 +
|
|}
|}

Revision as of 17:47, 19 October 2007

.:: An Engineer's View on Biological Learning ::.

Figure 1: Schematic view on the system implemented by logical gates.

An equivalent system behavior can be realized using [http://en.wikipedia.org/wiki/Flip-flop_%28electronics%29 flip-flops], implemented by [http://en.wikipedia.org/wiki/Logic_gate logical gates]:

As already shown in the finite state machine representation (FSM), the proposed system consists of three different states and recognizes four different inputs. In total, this adds up to twelve different transitions. In order to implement these twelve transitions with a digital system, at least four binary inputs are required (allowing for a maximum of 16 transitions) and since the proposed system has four different outputs, at least two binary outputs are needed. Here, we chose an implementation using two JK flip-flops consisting of [http://en.wikipedia.org/wiki/Nand_gate#NAND_gate NAND gates]. An overview of the resulting system is given in Fig. 1 and details concerning flip-flop and NAND gate behavior are given in the following table:

J K Qnext A B A NAND B
0 0 Qprev 0 0 1
0 1 0 0 1 1
1 0 1 1 0 1
1 1 [http://en.wikipedia.org/wiki/Inverse_%28logic%29 ¬]Qprev 1 1 0

When initializing the system we set both outputs Q to zero. The mapping from inputs (AHL+IPTG, IPTG, AHL+aTc, aTc) and system states (q0, q1, q2) to the binary inputs (J1, K1, J2, K2) is given by following table:

states/inputs AHL+IPTG IPTG AHL+aTc aTc
q0 J1=0, K1=1, J2=1, K2=0 J1=0, K1=0, J2=0, K2=1 J1=1, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=1
q1 J1=0, K1=1, J2=1, K2=0 J1=0, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=0 J1=0, K1=0, J2=1, K2=1
q2 J1=1, K1=0, J2=0, K2=0 J1=1, K1=1, J2=0, K2=0 J1=1, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=1

Here, we assume that the FSM system states q0, q1, q2 are mapped to the outputs Q1 and Q2 as follows:

FSM states/output coding Q1 Q2
J1=0, K1=1, J2=1, K2=0 J1=0, K1=0, J2=0, K2=1 J1=1, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=1 J1=0, K1=1, J2=1, K2=0 J1=0, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=0 J1=0, K1=0, J2=1, K2=1 J1=1, K1=0, J2=0, K2=0 J1=1, K1=1, J2=0, K2=0 J1=1, K1=0, J2=0, K2=1 J1=0, K1=1, J2=0, K2=1
green green red green green green yellow blue yellow yellow yellow yellow

The final mapping from transitions to the biological reporters is then given by:

Q1
Q2
Retrieved from "http://2007.igem.org/wiki/index.php/ETHZ/FlipFlop"