Tristable/Testing Constructs
From 2007.igem.org
< Tristable(Difference between revisions)
| (2 intermediate revisions not shown) | |||
| Line 119: | Line 119: | ||
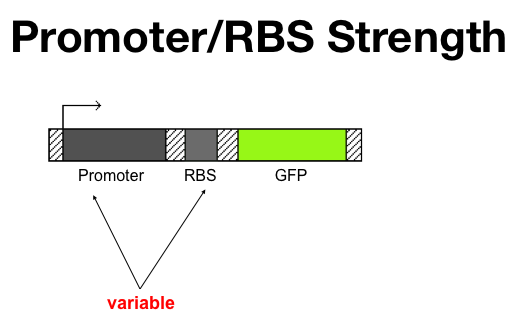
The full testing construct will look like: | The full testing construct will look like: | ||
| - | Constitutive Promoter>>RBS>> | + | Constitutive Promoter>>RBS>>Repressor of Interest>>Term |
| - | Promoter of Interest>>RBS>> | + | Promoter of Interest>>RBS>>Reporter>>Term |
| + | |||
| + | The respective ligand would be added to the system at t=0, repressor would fall off the operator region and Reporter would start to be produced. We would measure this production rate and determine alpha. | ||
| Line 137: | Line 139: | ||
===Cooperativity of Repression=== | ===Cooperativity of Repression=== | ||
The cooperativity describes an inherent characteristic of a repressor's repression. In our system we want to know how [[Image:betaTest.png|thumb|left|The Beta test Architecture]]much increased repressor concentration will increase repression. In our model, cooperativity is an exponent, beta, so that the repressor concentration is raised to the beta ([repressor]^beta = total repression). For beta = 1, repression increases linearly with repressor concentration. With twice as much repressor there is twice the repression. For beta = 2, repression increases with the square of the concentration. Twice as much repressor leads to four times the repression. Our model predicts that our system will be more robust with greater beta values and the tri stable region (in the graph) will be larger. Betas must be larger than one for the system to be stable. | The cooperativity describes an inherent characteristic of a repressor's repression. In our system we want to know how [[Image:betaTest.png|thumb|left|The Beta test Architecture]]much increased repressor concentration will increase repression. In our model, cooperativity is an exponent, beta, so that the repressor concentration is raised to the beta ([repressor]^beta = total repression). For beta = 1, repression increases linearly with repressor concentration. With twice as much repressor there is twice the repression. For beta = 2, repression increases with the square of the concentration. Twice as much repressor leads to four times the repression. Our model predicts that our system will be more robust with greater beta values and the tri stable region (in the graph) will be larger. Betas must be larger than one for the system to be stable. | ||
| + | |||
| + | |||
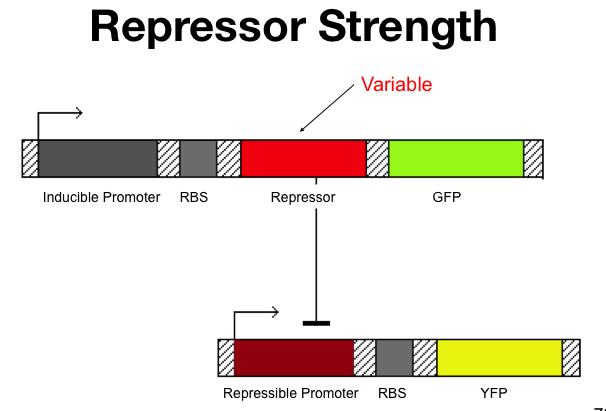
| + | The full testing construct looks like: | ||
| + | |||
| + | |||
| + | Constitutive Promoter>>RBS>>LuxR>>Term | ||
| + | |||
| + | pLux>>RBS>>Repressor of Interest>>RBS>>Reporter1>>Term | ||
| + | |||
| + | Promoter of Interest>>RBS>>Reporter2>>Term | ||
| + | |||
| + | Initially the Repressor would be off and Reporter2 would be on. Then when AHL is added at varying concentrations, the repressor and Reporter1 are synthesized. Reporter1 concentration will increase linearly with Repressor so we will compare the Reporter1 vs. Reporter2, fit a curve the relation and determine to what power Reporter1 decreases, the beta value. | ||
| + | |||
Latest revision as of 06:54, 25 October 2007