Valencia/Electronic comparator

From 2007.igem.org

< Valencia(Difference between revisions)
 
(3 intermediate revisions not shown)
Line 1: Line 1:
{{Valencia/Cabecera}}
{{Valencia/Cabecera}}
-
The basis of our [[Valencia/Comparator | biological comparator]], is the digital comparator. All our project, consist in transform the system of an electronic comparator in a biological process which behavior must represent the function of a comparator.
+
 
-
With the aim to understand how our biological comparator should be, first we must study how an electronic comparator works.
+
The basis of our [[Valencia/Comparator | biological comparator]], is the digital comparator. All our project consist on transforming the system of an electronic comparator in a biological process which behavior must represent the function of a comparator.
 +
With the aim of understanding how our biological comparator should be, first we must study how an electronic comparator works.
==The comparator function==
==The comparator function==
To start with we must know how it's going to work. We must work with binary because its an electronic device, and its inputs and outputs will be 0 or 1. In our case, 0 and 1 represents False and True.
To start with we must know how it's going to work. We must work with binary because its an electronic device, and its inputs and outputs will be 0 or 1. In our case, 0 and 1 represents False and True.
-
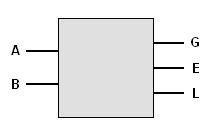
Let be the inputs A and B, and the outputs G, E and L, for Greater, Equal, and Less.
+
Let the inputs be A and B, and the outputs G, E and L, for Greater, Equal, and Lower.
[[Image:VCompgel.jpg|thumb|200px|Basic Inputs/Outputs of the comparator|right]]
[[Image:VCompgel.jpg|thumb|200px|Basic Inputs/Outputs of the comparator|right]]
Line 16: Line 17:
*If A < B, (A less than B), L=1 and the rest 0
*If A < B, (A less than B), L=1 and the rest 0
-
Is usually represent these conditions in a Truth Table
+
We usually represent these conditions in a Table of Truth.
{| border="1"
{| border="1"
Line 51: Line 52:
|}  
|}  
-
So, we can construct the mathematical conditions to find the proper logic gates and construct our device.
+
So, we can set the mathematical conditions to find the proper logic gates and construct our device.
[[Image:VComparts.jpg|thumb|300px|Diagram with logic gates of the comparator|right]]
[[Image:VComparts.jpg|thumb|300px|Diagram with logic gates of the comparator|right]]
#G is True when A>B. A=1, B=0
#G is True when A>B. A=1, B=0
Line 60: Line 61:
#*L=A'·B
#*L=A'·B
-
We suppose known the equivalences between the mathematical operators and the logic gates.
+
We suppose that we know the equivalences between the mathematical operators and the logic gates.
-
The (') is the gate NOT, which switch 1 and 0; the operation (·) is the AND gate; and the equation for E, is the formula for the XNOR gate. So is easy construct the electronic diagram with this information.
+
The (') is the gate NOT, which switch 1 and 0; the operation (·) is the AND gate; and the equation for E, is the formula for the XNOR gate. So it is easy to construct the electronic diagram with this information.
==For more information==
==For more information==

Latest revision as of 15:11, 26 October 2007

VBacteriaAnimada.gif
Summary The idea Promoter calibrator Biological comparator Electronic comparator Biological controller Lab Work Silico Work Results Adversities


The basis of our biological comparator, is the digital comparator. All our project consist on transforming the system of an electronic comparator in a biological process which behavior must represent the function of a comparator. With the aim of understanding how our biological comparator should be, first we must study how an electronic comparator works.

The comparator function

To start with we must know how it's going to work. We must work with binary because its an electronic device, and its inputs and outputs will be 0 or 1. In our case, 0 and 1 represents False and True. Let the inputs be A and B, and the outputs G, E and L, for Greater, Equal, and Lower.

Basic Inputs/Outputs of the comparator

The comparator works like this:

  • If A > B, (A is grater than B),we get G=1, and 0 at E and L.
  • If A = B, (A equal to B), E=1 and the rest 0.
  • If A < B, (A less than B), L=1 and the rest 0

We usually represent these conditions in a Table of Truth.

 A   B   G   E   L 
 0   0   0   1   0 
 1   0   1   0   0 
 0   1   0   0   1 
 1   1   0   1   0 

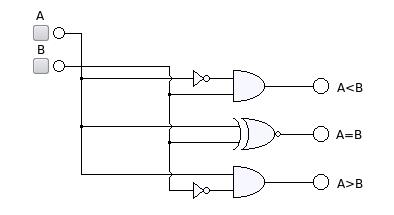
So, we can set the mathematical conditions to find the proper logic gates and construct our device.

Diagram with logic gates of the comparator
  1. G is True when A>B. A=1, B=0
    • G=A·B'
  2. E is True when A=B. Two cases A=B=0 or A=B=1.
    • E=A'·B'+A·B
  3. L is True when A<B. A=0, B=1
    • L=A'·B

We suppose that we know the equivalences between the mathematical operators and the logic gates. The (') is the gate NOT, which switch 1 and 0; the operation (·) is the AND gate; and the equation for E, is the formula for the XNOR gate. So it is easy to construct the electronic diagram with this information.

For more information

  • [http://en.wikipedia.org/wiki/Comparator Comparator]
  • [http://en.wikipedia.org/wiki/Logic_gate Logic Gate]
  • [http://en.wikipedia.org/wiki/Truth_table Truth Table]

In Spanish

  • [http://es.wikipedia.org/wiki/Puerta_l%C3%B3gica Puerta Logica]
  • [http://es.wikipedia.org/wiki/Circuito_comparador Comparador]
  • [http://es.wikipedia.org/wiki/Tabla_de_verdad Tabla de Verdad]
Retrieved from "http://2007.igem.org/wiki/index.php/Valencia/Electronic_comparator"