Rice/Project A: Phage Project
From 2007.igem.org
Tstevenson (Talk | contribs) (→'''Experimental Construction of the Circuit''') |
(→'''Results''') |
||
| (21 intermediate revisions not shown) | |||
| Line 7: | Line 7: | ||
==== '''Motivation''' ==== | ==== '''Motivation''' ==== | ||
| - | Bacteria are 'cleverer' than they seem at first glance! As humans dump antibiotic agents on these tiny disease causing microbes, they evolve strategies to evade these drugs. Since the discovery of penicillin by Alexander Fleming, more potent drugs with the ability to neutralize a wider spectrum of microbes have been invented and used. As the disease treatment strategies harbor on use | + | Bacteria are 'cleverer' than they seem at first glance! As humans dump antibiotic agents on these tiny disease causing microbes, they evolve strategies to evade these drugs. Since the discovery of penicillin by Alexander Fleming, more potent drugs with the ability to neutralize a wider spectrum of microbes have been invented and used. As the disease treatment strategies harbor on use of more effective drug regimens, bacteria evolve their ability to evade death, setting up an 'arms-race' between bacterial antibiotic resistance and multi-drug combinations used to combat resistance of the disease-causing pathogen. |
[[Image:kishony paper snapshot.jpg|thumb|'''Kishony paper snapshot'''|200px|right|Antbiotic interactions that select against resistance]] | [[Image:kishony paper snapshot.jpg|thumb|'''Kishony paper snapshot'''|200px|right|Antbiotic interactions that select against resistance]] | ||
| - | Application of an antibiotic affects the adversity of growth environment of | + | Application of an antibiotic affects the adversity of the growth environment of bacteria. Following principles of population ecology, competition for common essential resources between two subsets of a genetically identical population leads to application of selective pressure. Development of antibiotic resistance is a consequence of evolutionary adaptation by natural selection favoring bacteria that are able to withstand the environmental pressure brought on by the antibiotic. Such '''resistance''' generally develops by one of the following ways: |
| - | '''1. Drug inactivation or modification''': | + | '''1. Drug inactivation or modification''': Production of an enzyme that destroys the drug, such as enzymatic deactivation of penicillin G in some penicillin-resistant bacteria through the production of β-lactamases. |
| - | '''2. Alteration of structural target''': | + | '''2. Alteration of structural target''': Alteration of penicillin binding proteins by beta lactams, alteration of topoisomerases by quinolones, and ribosomal proteins by amino-glycosides. |
| - | '''3. Alteration of metabolic | + | '''3. Alteration of metabolic pathways''': Unlike bacteria inhibited by sulfonamides, some sulfonamide-resistant bacteria do not require para-aminobenzoic acid (PABA). Instead, like mammalian cells, they utilize preformed folic acid. |
| - | '''4. Reduced drug accumulation''' : | + | '''4. Reduced drug accumulation''' : Decreasing cell permeability to the drug by mutations in components in the cell wall or structure of porins, and/or increasing active efflux of the drug from the cytoplasm by mutations in the efflux pump. |
Development of multi-drug resistance comes about by either one or a combination of these '''mechanisms''' and is conferred by: | Development of multi-drug resistance comes about by either one or a combination of these '''mechanisms''' and is conferred by: | ||
| - | '''1. Development of mutational resistance''': Mutations in genes affecting | + | '''1. Development of mutational resistance''': Mutations in genes affecting any of the 4 processes mentioned above. |
'''2. Transfer or acquisition of resistance''': Transfer from one bacteria to another. | '''2. Transfer or acquisition of resistance''': Transfer from one bacteria to another. | ||
| - | '''Conventional strategies''' to counter the problem of multi-drug resistance include use of large amounts of | + | '''Conventional strategies''' to counter the problem of multi-drug resistance include the use of large amounts of potent, multi-spectrum antibiotics; the development of novel antibiotics targeting hitherto underutilized targets; and the use of a combination of mutually antagonistic antibiotics. These methods tend to be expensive, cause multiple harmful side effects in the patient, and require a long time to implement. |
| - | [[Image:overall_idea.jpg|thumb|400px|right|'''A.''' Changing the fitness landscape of an ''E. | + | [[Image:overall_idea.jpg|thumb|400px|right|'''A.''' Changing the fitness landscape of an ''E. Coli'' population upon application of the tetracycline antibiotic.]] |
| - | [[ | + | '''[[Roy Kishony's lab]]''' at Harvard played 'evolutionary competition games' to determine how differential selection between antibiotic resistant and sensitive bacterial populations is affected under a regime of multiple drug combinations. Normally, if two populations of the same bacterial strain compete, the one that mutated to acquire antibiotic resistance 'wins' the fight for survival. However, by using a direct competition assay between Doxycycline resistant and Doxycycline sensitive ''E. coli'' under a particular regime of antagonistic antibiotic combinations, '''[[Chet et. al.]]''' demonstrate that the bacterial population harboring resistance is selected against in preference to the sensitive population. They find that in drug combination regimens that involve suppressive interactions, high drug concentrations result in competitive selection against resistance without perturbing the effectiveness of the other drug in the combination. These results are interpreted as coming from a trade-off regime in the evolution of resistance fitness landscape, where absolute potency of a drug combination is balanced by the relative competitive selection imposed on emerging resistant populations. Identification of reciprocally suppressive drug combinations in which each drug also imposes selection pressures against the resistance developed to the other can be harnessed to counteract rapid development of multi-drug resistance. |
| - | + | [[Image:Phage_immunity_antibiotic.jpg|thumb|400px|right|'''B.''' Coupling tetracycline sensitivity of an ''E. coli'' to its ability to switch between lysis and lysogeny and immunity to phage.]] | |
| - | + | Following up on this body of work, '''our iGEM team''' asked the following question: Can we artificially engineer a bacterial strain that would lead to selection against antibiotic resistance in a bacterial population? In other words, given the existence of 'selection against antibiotic resistance', can we reverse-engineer a system to recapitulate that specific fitness regime? | |
| - | + | ||
| - | Following up on this body of work, '''our iGEM team''' asked the following question: Can we artificially engineer a bacterial strain that would lead to | + | |
==== '''Goals''' ==== | ==== '''Goals''' ==== | ||
| - | By conferring selective advantage on bacterial population, we intend to artificially create changes in evolutionary fitness landscape | + | By conferring selective advantage on a bacterial population, we intend to artificially create changes in the evolutionary fitness landscape so that bacteria harboring antibiotic resistance are out-competed. We will take advantage of the following: |
1. Antibiotic as a signaling molecule | 1. Antibiotic as a signaling molecule | ||
| Line 49: | Line 47: | ||
3. 'Immunity' of bacterial strain to lambda phage infection | 3. 'Immunity' of bacterial strain to lambda phage infection | ||
| - | 4. | + | 4. Correlation of sensitivity to antibiotic concentration with lysis versus lysogeny decision in phage infected bacteria. |
<BR> | <BR> | ||
| + | |||
== '''Experimental System and Circuit Design''' == | == '''Experimental System and Circuit Design''' == | ||
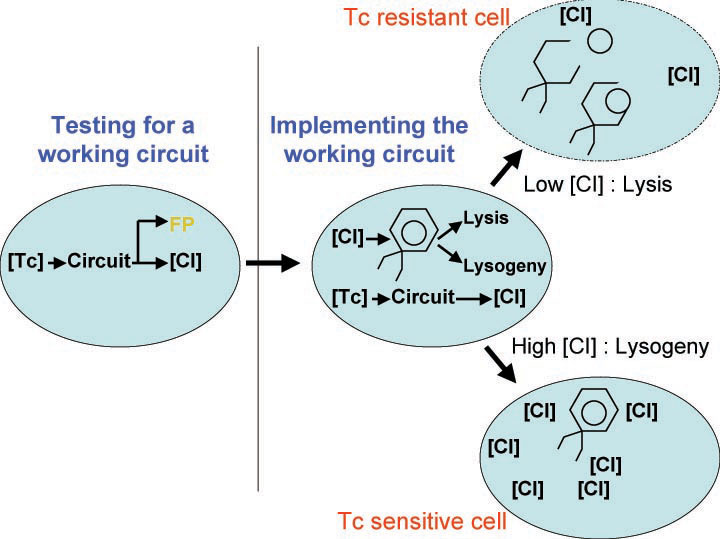
| - | In order to set the stage for playing evolutionary competition games, we first engineer a bacterial population consisting of ''E.coli'' cells that are either sensitive or resistant to the application of the antibiotic tetracycline. Our goal is to make | + | In order to set the stage for playing evolutionary competition games, we first engineer a bacterial population consisting of ''E. coli'' cells that are either sensitive or resistant to the application of the antibiotic tetracycline. Our goal is to make tetracycline sensitive cells more fit than tetracycline resistant cells. The ability to survive increasing concentrations of tetracycline is used as a measure of fitness. This idea is summarized in the Figures A and B: |
[[Image:circuit_overview.jpg|thumb|500px|right|'''C.''' Modular parts of the circuit to be constructed.]] | [[Image:circuit_overview.jpg|thumb|500px|right|'''C.''' Modular parts of the circuit to be constructed.]] | ||
| - | '''MIC''': | + | '''MIC''': The lowest concentration of an antimicrobial that will inhibit the visible growth of a microorganism after overnight incubation. Minimum inhibitory concentrations are important in laboratory culture conditions to confirm resistance of microorganisms to an antimicrobial agent and to monitor the activity of new antimicrobial agents. |
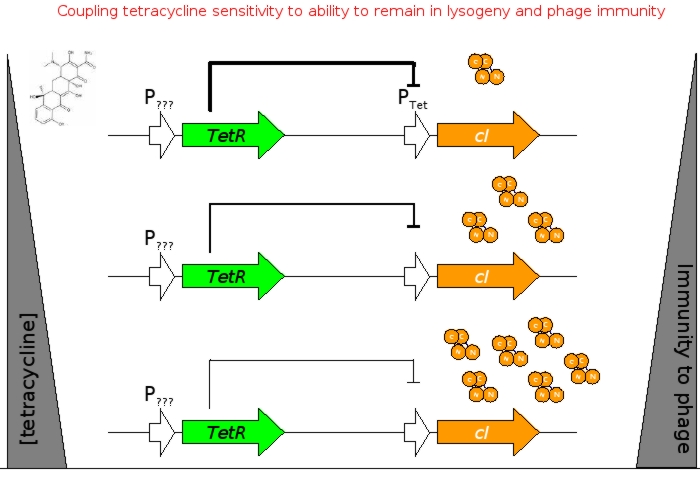
| - | A bacterial cell infected with | + | A bacterial cell infected with bacteriophage lambda regulates the lysis versus lysogeny choice by modulating the amount of lambda repressor produced. High lambda repressor downregulates phage genes and concurrently upregulated its own genes that allow it to remain in lysogeny. However, the lysis pathway switch is flipped on upon decrease of lambda repressor. This is brought about by induction by exposure to UV, which causes an increase of Cro protein. It follows that increased immunity to lambda can be induced by increasing concentration of the lambda repressor, allowing the bacteria to remain in lysogeny. We simultaneously couple the lytic-lysogeny switch to tetracycline induced transcription of lambda repressor as well as tetracycline induced antibiotic resistance to comparison of fitness between resistant and sensitive cells. By this coupling, we want to tune the parameters in our system so that we land in a fitness regime that will confer selective advantage to the tetracycline sensitive cells, simultaneously selecting againt tetracycline resistant cells. This idea is summarized in Figure D: |
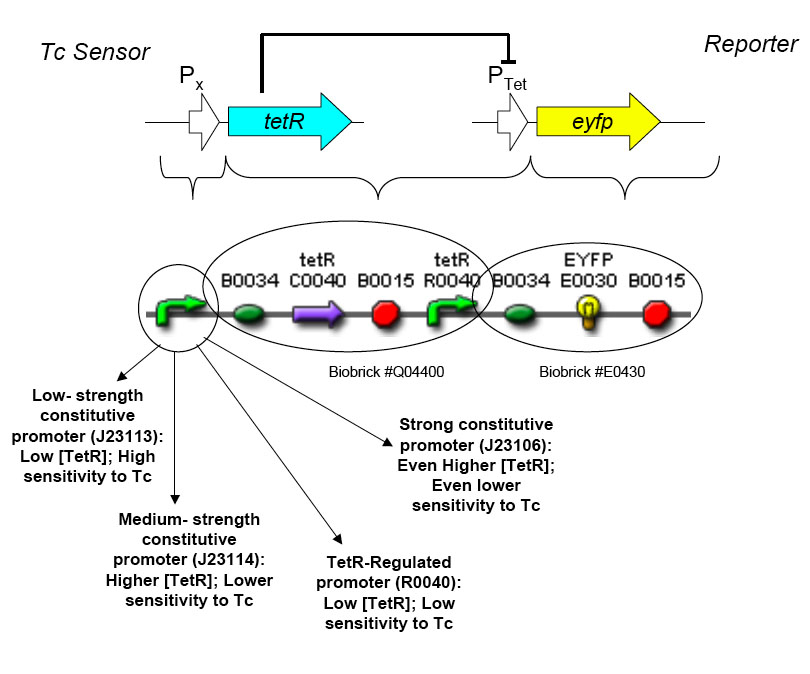
| - | [[Image:tet_sensor.jpg|thumb|500px|right|'''D.''' Output of the circuit to presence or absence of | + | [[Image:tet_sensor.jpg|thumb|500px|right|'''D.''' Output of the circuit to presence or absence of tetracycline.]] |
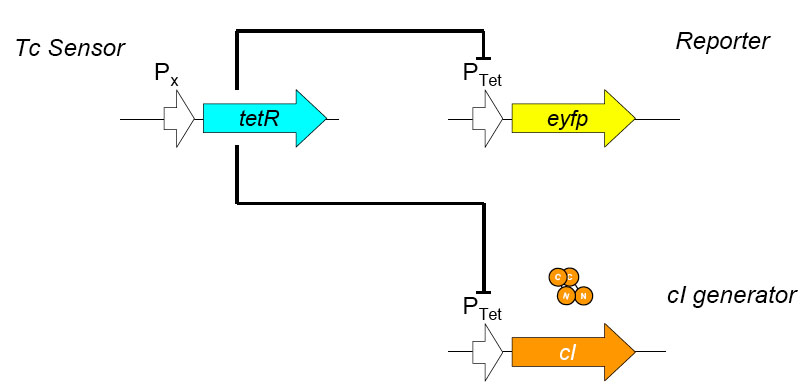
| - | '''Basic Circuit Design''' - The general strategy for linking lysis to tetracycline resistance | + | '''Basic Circuit Design''' - The general strategy for linking lysis to tetracycline resistance involves putting a lambda transcription factor (CI) under control of the Tet promoter. This circuit causes the amount of CI in a cell to be proportional to the amount of tetracycline in the cell. Cells with higher concentrations of tetracycline have higher levels of CI, thus preventing lysis of the cell via phage. Cells with lower levels of tetracycline (cells that are resistant to tetracycline) will have less CI present and thus be more susceptible to lysis by phage. |
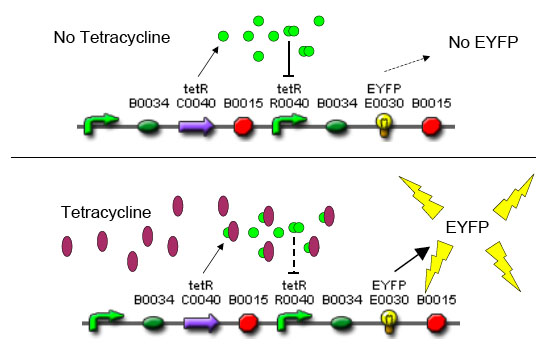
[[Image:tc sensor function.jpg|thumb|500px|right|'''E.''' Biobrick parts used in construction of the Tet sensor.]] | [[Image:tc sensor function.jpg|thumb|500px|right|'''E.''' Biobrick parts used in construction of the Tet sensor.]] | ||
| - | We designed the circuit keeping in mind the following | + | We designed the circuit keeping in mind the following goals: |
| - | * | + | * A circuit with existing BioBricks requiring few ligations to construct |
| - | * | + | * A design that could be used with multiple types of resistance |
| - | * | + | * A robust circuit that will remain stable for large numbers of generations |
| - | * | + | * A circuit that can propagate through bacterial populations, e.g., practical for treating environmental problems. |
| - | '''Antibiotic Selection''' - The antibiotic resistance we will be selecting against in this circuit will be tetracycline. | + | '''Antibiotic Selection''' - The antibiotic resistance we will be selecting against in this circuit will be tetracycline. Tetracycline was selected because the Tn10 tetracycline resistance transposon has been extremely well characterized and can be activated by a non-antibiotic molecule anhydrotetracycline (ATc) that binds to the TetR transcription factor, allowing us to use a variety of approaches when characterizing the genetic circuit. TetA, the tetracycline efflux pump coded for by Tn10, is toxic to cells. As a result, under conditions of low or no tetracyline, the tetracycline sensitive cells will already have a slight advantage over the tetracycline resistant cells, which will reduce the amount of tuning required for this circuit. Furthermore, the human body is extremely tolerant of tetracycline, making it a good target for resistance reduction. |
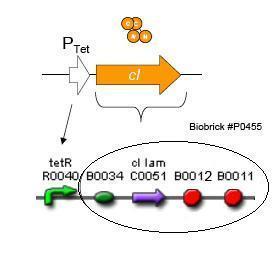
| - | [[Image:Lambda CI generator.jpg|thumb|250px|right|'''F.''' | + | [[Image:Lambda CI generator.jpg|thumb|250px|right|'''F.''' Biobrick parts used in construction of the Lambda Generator.]] |
| - | '''Strain Selection''' – To compare the relative fitness of tetracycline resistant versus that of tetracycline sensitive phage infected cells, we selected two strains of ''E.coli'' genotypically identical with the exception that one has the Tn10 tetracyline resistance transposon ( | + | '''Strain Selection''' – To compare the relative fitness of tetracycline resistant cells versus that of tetracycline sensitive phage infected cells, we selected two strains of ''E. coli'' genotypically identical with the exception that one has the Tn10 tetracyline resistance transposon. GNB824 (tetracycline resistant) is a derivative GNB8385K (tetracycline sensitive) that had the Tn10 transposon incorporated genomically. Tn10 incorporation was screened for by assaying loss of regulation of the lysine decarboxylase loci, resulting in pH independent production of lysine decarboxylase (cells with properly incorporated transposon turn red on MacConkey agar). These nearly identical strains will allow us to assess the impact of tetracycline resistance on relative fitness. |
| - | '''Bacteriophage Selection''' - When selecting the bacteriophage to be used in this circuit, we desired a phage whose life cycle and genome had been well characterized. Bacteriophage lambda has all of | + | '''Bacteriophage Selection''' - When selecting the bacteriophage to be used in this circuit, we desired a phage whose life cycle and genome had been well characterized. Bacteriophage lambda has all of this characteristics as well as the benefit of being commonly used as a cloning vector. Specifically, the lambda strain we selected can be induced to undergo lytic growth by growing lysogenic cells at 42°C. Also, due to the infectious nature of bacteriophage lambda, we selected a strain that is unable to lyse cells (amber mutation prevents the expression of lytic enzyme, protecting other bacteria within the lab from phage infection). Though the phage will not lyse the cells, it will produce fully functional phage particles that can be isolated via chloroform extraction. |
| - | '''Phage Engineering''' – We will construct a recombination plasmid designed to integrate our circuit into lambda DNA located chromosomally in lysogen ''E.coli''. The plasmid will not contain an origin of replication (to limit recombination sites), so we will have to amplify it using high fidelity PCR. | + | '''Phage Engineering''' – We will construct a recombination plasmid designed to integrate our circuit into lambda DNA located chromosomally in lysogen ''E. coli''. The plasmid will not contain an origin of replication (to limit recombination sites), so we will have to amplify it using high fidelity PCR. The plasmid will contain our circuit flanked by homologous recombination sites that will combine at a non-critical location of the phage chromosome (yet to be determined). Within this homologous recombination site, we will construct a BioBrick restriction site, allowing us to integrate any BioBrick part into the lambda phage genome. |
| - | '''Circuit Characterization''' – To assay relative fitness of the cells, we will measure doubling times of the strains at sub-MIC | + | '''Circuit Characterization''' – To assay relative fitness of the cells, we will measure doubling times of the strains at sub-MIC tetracycline by measuring optical density (600nm) of cells. |
==== '''Experimental Materials and Methods ''' ==== | ==== '''Experimental Materials and Methods ''' ==== | ||
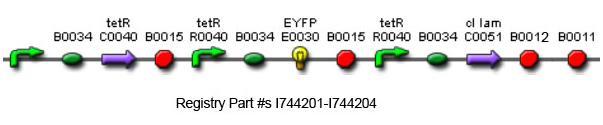
| - | The overall '''construction scheme''' with the modular parts of the circuit is | + | The overall '''construction scheme''' with the modular parts of the circuit is shown in Figure C. Differential response to exposure to tetracycline is schematized in Figure D. Biobrick parts used in the circuit are shown in Figure E. |
==== '''Testing and Characterization of the Constructed Circuit''' ==== | ==== '''Testing and Characterization of the Constructed Circuit''' ==== | ||
| - | Using promoters of different strengths, the circuit has been characterized for its ability to grow in various concentrations of | + | Using promoters of different strengths, the circuit has been characterized for its ability to grow in various concentrations of tetracycline. The EYFP fluorescent reporter serves as a readout for the functionality of the circuit as a Tet sensor. The Lambda Generator part is described in Figure F. The final circuit is presented below, in Figure G. |
[[Image:full_circuit_biobrick.jpg|thumb|600px|center|'''G.'''The complete Biobricks circuit.]] | [[Image:full_circuit_biobrick.jpg|thumb|600px|center|'''G.'''The complete Biobricks circuit.]] | ||
| + | |||
| + | ==== '''Constructs Submitted and Verified''' ==== | ||
| + | |||
| + | [[Image:PartsTable.jpg]] | ||
<BR> | <BR> | ||
| Line 106: | Line 109: | ||
We use stochastic differential equations to represent chemical reactions with each reacting species being a component of the circuit. Numerical solutions are obtained by the '''[[Gillespie Stochastic Simulation Algorithm]]''', implemented in Matlab. Here is the [[code]] used. Figure H shows the reactions used in the modeling. | We use stochastic differential equations to represent chemical reactions with each reacting species being a component of the circuit. Numerical solutions are obtained by the '''[[Gillespie Stochastic Simulation Algorithm]]''', implemented in Matlab. Here is the [[code]] used. Figure H shows the reactions used in the modeling. | ||
| - | The Gillespie algorithm is used to perform a discrete stochastic simulation of a system of well mixed reactant molecules wherein the 'fate trajectory' of each molecule is explicitly simulated. A Gillespie simulation is a random walk that exactly represents the distribution of the Chemical Master Equation. The physical interpretation of the Simulation is that individual molecules participating as reactants in a system undergo frequent collisions, a sub-set of which are collisions that are in correct stereo-chemical orientation and with sufficient potential energy. In a Gillespie Simulation exercise, a well mixed reaction environment is presumed. Each of the participating species | + | The Gillespie algorithm is used to perform a discrete stochastic simulation of a system of well mixed reactant molecules wherein the 'fate trajectory' of each molecule is explicitly simulated. A Gillespie simulation is a random walk that exactly represents the distribution of the Chemical Master Equation. The physical interpretation of the Simulation is that individual molecules participating as reactants in a system undergo frequent collisions, a sub-set of which are collisions that are in correct stereo-chemical orientation and with sufficient potential energy. In a Gillespie Simulation exercise, a well mixed reaction environment is presumed. Each of the participating species is explicitly traced so that (a) which reaction will occur at the next time step and (b) the probability of a reaction occurring at the next time step is known. The Gillespie method of stochastic simulation is advantageous over the deterministic differential equation based modeling of chemical reactions assuming mass action kinetics because it does not approximate chemical reactions as occurring in bulk but rather accounts for a chemical reaction occurring between two chemical species. |
[[Image:Model_SSAequations.jpg|thumb|400px|right|'''H.''' Chemical Equations used in the Gillespie SSA solution]] | [[Image:Model_SSAequations.jpg|thumb|400px|right|'''H.''' Chemical Equations used in the Gillespie SSA solution]] | ||
| Line 112: | Line 115: | ||
The following '''assumptions''' are made: | The following '''assumptions''' are made: | ||
| - | * Any spatial aspects of the modeling problem | + | * Any spatial aspects of the modeling problem are ignored (i.e. Gillespie is only running in time) |
* Parameter values are input from the following references: | * Parameter values are input from the following references: | ||
| Line 120: | Line 123: | ||
**Sotiropoulos, V. and Kaznessis, Y. N. Synthetic tetracycline-inducible regulatory networks: computer-aided design of dynamic phenotypes. BMC Systems Biology. Jan 2009. | **Sotiropoulos, V. and Kaznessis, Y. N. Synthetic tetracycline-inducible regulatory networks: computer-aided design of dynamic phenotypes. BMC Systems Biology. Jan 2009. | ||
| - | * Steps in gene expression i.e. transcription and translation are simplified by not modeling RNAP binding/unbinding to the promoter and Ribsome binding/unbinding; modified propensities are used from the reference above. | + | * Steps in gene expression (i.e. transcription and translation) are simplified by not modeling RNAP binding/unbinding to the promoter and Ribsome binding/unbinding; modified propensities are used from the reference above. |
* Growth rates are assumed not to vary among cell types (i.e. infected vs. non-infected). | * Growth rates are assumed not to vary among cell types (i.e. infected vs. non-infected). | ||
| Line 128: | Line 131: | ||
* The propensities for tetA is recovered from experimental data in the literature. | * The propensities for tetA is recovered from experimental data in the literature. | ||
| - | For the circuit constructed, one of the possible readouts of 'measure of fitness' in the wake of | + | For the circuit constructed, one of the possible readouts of 'measure of fitness' in the wake of tetracycline exposure would be the amount of CI produced. Through the simulations, we trace the time evolution profiles of CI production and compare the results in Tet-sensitive and Tet-resistant cells. We infer that the probability of a population of Tet-resistant ''E. coli'' cells going into lysis over the choice to remain in lysogenic state increases after tetracycline challenge. |
<BR> | <BR> | ||
| + | |||
== '''Results''' == | == '''Results''' == | ||
| + | |||
==== '''Predictive Modeling of the Circuit''' ==== | ==== '''Predictive Modeling of the Circuit''' ==== | ||
| - | The modeling | + | The modeling exercise provided us with a proof-of-principle that it should be possible to engineer production of lambda repressor under the control of Tetracycline such that Tetracycline resistant cells are under a fitness disadvantage regime and are out competed by the Tetracycline sensitive cells. From this model, we intend to extract the follwing information: |
* Concentration profile of Tetracycline necessary for induction of the circuit. | * Concentration profile of Tetracycline necessary for induction of the circuit. | ||
| Line 141: | Line 146: | ||
* The probability of lysis given a specific induction of the circuit by tetracycline. | * The probability of lysis given a specific induction of the circuit by tetracycline. | ||
| + | The modeling exercise provided us a proof of principle that it should be possible to engineer production of lambda repressor under the control of tetracycline such that tetracycline resistant cells are under a fitness disadvantage regime and are out competed by the tetracycline sensitive cells (Figure I). | ||
| - | ==== ''' | + | Before, the full scale simulation was run, preliminary models were run in order to better understand the results of the different plasmid constructs. These experimental results helped to fine tune the parameters of the model. This refined model could then predict the dynamic of the engineered circuit within the phage genome in order to understand the effects of stochasticity and gene copy number on the efficacy of the circuit's ability to decrease the fitness of resistant cells (Figure J). |
| - | [[Image:Tableoparts.jpg|thumb| | + | |
| + | In the early stages of designed the circuit, the negative feedback on TetR expression was added in order to decease the noise in the circuit and to provide more stable expression levels of TetR for varying gene copy numbers as predicted by the preliminary model. | ||
| + | |||
| + | Later, we used the model to analyze the effects of altering the strength of cI repression by TetR as well as the negative feedback of TetR. | ||
| + | |||
| + | [[Image:modeling_output_schematic.jpg|thumb|'''modeling_output_schematic'''|400px|right|I. Schematic of modeling output]] | ||
| + | |||
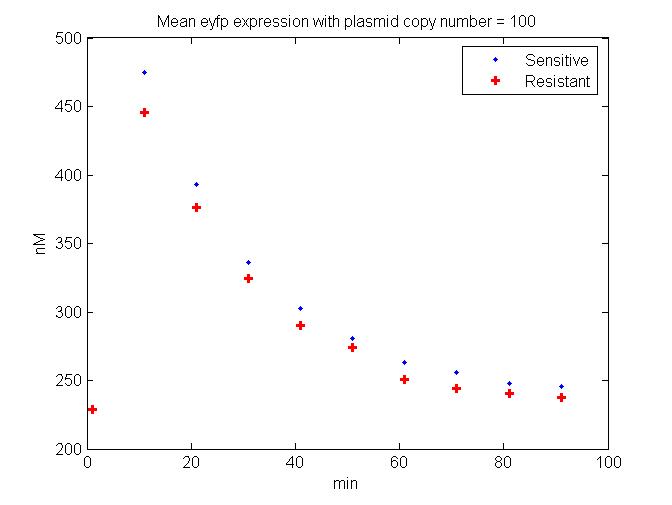
| + | [[Image:HighPlasmidMeanEyfp.jpg.jpg|thumb|'''HighPlasmidMeanEyfp'''|400px|right|J. Difference between Single Cell Fluorescence levels in Tet sensitive versus resistant cells. The example showin in the model has a plasmid copy number of 100 per bacterial cell (of the circuit shown in Figure C and the readout is EYFP fluorescence]] | ||
| + | |||
| + | ==== '''Characterization of the Circuit''' ==== | ||
| + | |||
| + | |||
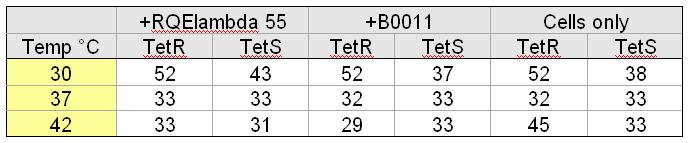
| + | [[Image:Tableoparts.jpg|thumb|right|500px| K. Cells were cultured in LB. +RQEλ55 and +B0011 cells were cultured with 50ug/mL ampicillin. Doubling time was found by measuring optical density (OD600nm) of cultures at hour intervals for five hours.]] | ||
The doubling times listed in the table to the left provide the relative fitness of TetS and TetR cells grown at different temperatures containing different circuits. The data indicate that, at 37 degrees C, our circuit does not impact the doubling time of TetR or TetS cells. | The doubling times listed in the table to the left provide the relative fitness of TetS and TetR cells grown at different temperatures containing different circuits. The data indicate that, at 37 degrees C, our circuit does not impact the doubling time of TetR or TetS cells. | ||
| Line 149: | Line 167: | ||
<BR> | <BR> | ||
| - | [[Image:FluorescentData.jpg|thumb|right|500px| Top: Averaged fluorescent data of taken from four M9 minimal media cultures of TetS+RQEλ55 and TetS+B0011 over the course of 90 minutes. The excitation and emission wavelengths used to measure fluorescence were 514nm and 527nm respectively. Bottom:Averaged fluorescent data of taken from four M9 minimal media cultures of TetR+RQEλ55 and TetR+B0011 over the course of 90 minutes. The excitation and emission wavelengths used to measure fluorescence were 514nm and 527nm respectively.]] | + | [[Image:FluorescentData.jpg|thumb|right|500px|L. Top: Averaged fluorescent data of taken from four M9 minimal media cultures of TetS+RQEλ55 and TetS+B0011 over the course of 90 minutes. The excitation and emission wavelengths used to measure fluorescence were 514nm and 527nm respectively. Bottom:Averaged fluorescent data of taken from four M9 minimal media cultures of TetR+RQEλ55 and TetR+B0011 over the course of 90 minutes. The excitation and emission wavelengths used to measure fluorescence were 514nm and 527nm respectively.]] |
| - | + | ||
| + | |||
| + | Figure K and L measures the relative fluorescence of TetR and TetS cells with and without our circuit. The cells were cultured at 37 degrees C in M9 minimal media with 50ug/mL ampicillin and 1uM ATc. 1uM ATc is assumed to fully induce our circuit and produce a bolus of EYFP and CI in both TetS and TetR cells. The effectiveness of our circuit will be determined by the ratio of the fluorescence produced by TetS TetR. A high TetS/TetR ratio indicates that TetS cells are producing much more CI than the TetR cells, making any TetS lysogen much less likely to go into lytic phase. The data show that the fluorescence levels of TetR+RQEλ55 + are negligible when compared to the autofluorescence of TetR+B0011 while TetS+RQEλ55 produces a noticeable amount of fluorescence when compared to the TetS+B0011. At 100% induction, it appears that our circuit it binary. TetS+RQEλ55 cells will produce EYFP and CI while TetR+RQEλ55 produce almost no EYFP and CI. | ||
<BR> | <BR> | ||
== '''Milestones Accomplished''' == | == '''Milestones Accomplished''' == | ||
| + | |||
| + | Watch out for our presentation and poster at the Jamboree! | ||
Latest revision as of 03:57, 27 October 2007
Contents |
Phage Project
Background
Motivation
Bacteria are 'cleverer' than they seem at first glance! As humans dump antibiotic agents on these tiny disease causing microbes, they evolve strategies to evade these drugs. Since the discovery of penicillin by Alexander Fleming, more potent drugs with the ability to neutralize a wider spectrum of microbes have been invented and used. As the disease treatment strategies harbor on use of more effective drug regimens, bacteria evolve their ability to evade death, setting up an 'arms-race' between bacterial antibiotic resistance and multi-drug combinations used to combat resistance of the disease-causing pathogen.
Application of an antibiotic affects the adversity of the growth environment of bacteria. Following principles of population ecology, competition for common essential resources between two subsets of a genetically identical population leads to application of selective pressure. Development of antibiotic resistance is a consequence of evolutionary adaptation by natural selection favoring bacteria that are able to withstand the environmental pressure brought on by the antibiotic. Such resistance generally develops by one of the following ways:
1. Drug inactivation or modification: Production of an enzyme that destroys the drug, such as enzymatic deactivation of penicillin G in some penicillin-resistant bacteria through the production of β-lactamases.
2. Alteration of structural target: Alteration of penicillin binding proteins by beta lactams, alteration of topoisomerases by quinolones, and ribosomal proteins by amino-glycosides.
3. Alteration of metabolic pathways: Unlike bacteria inhibited by sulfonamides, some sulfonamide-resistant bacteria do not require para-aminobenzoic acid (PABA). Instead, like mammalian cells, they utilize preformed folic acid.
4. Reduced drug accumulation : Decreasing cell permeability to the drug by mutations in components in the cell wall or structure of porins, and/or increasing active efflux of the drug from the cytoplasm by mutations in the efflux pump.
Development of multi-drug resistance comes about by either one or a combination of these mechanisms and is conferred by:
1. Development of mutational resistance: Mutations in genes affecting any of the 4 processes mentioned above.
2. Transfer or acquisition of resistance: Transfer from one bacteria to another.
Conventional strategies to counter the problem of multi-drug resistance include the use of large amounts of potent, multi-spectrum antibiotics; the development of novel antibiotics targeting hitherto underutilized targets; and the use of a combination of mutually antagonistic antibiotics. These methods tend to be expensive, cause multiple harmful side effects in the patient, and require a long time to implement.
Roy Kishony's lab at Harvard played 'evolutionary competition games' to determine how differential selection between antibiotic resistant and sensitive bacterial populations is affected under a regime of multiple drug combinations. Normally, if two populations of the same bacterial strain compete, the one that mutated to acquire antibiotic resistance 'wins' the fight for survival. However, by using a direct competition assay between Doxycycline resistant and Doxycycline sensitive E. coli under a particular regime of antagonistic antibiotic combinations, Chet et. al. demonstrate that the bacterial population harboring resistance is selected against in preference to the sensitive population. They find that in drug combination regimens that involve suppressive interactions, high drug concentrations result in competitive selection against resistance without perturbing the effectiveness of the other drug in the combination. These results are interpreted as coming from a trade-off regime in the evolution of resistance fitness landscape, where absolute potency of a drug combination is balanced by the relative competitive selection imposed on emerging resistant populations. Identification of reciprocally suppressive drug combinations in which each drug also imposes selection pressures against the resistance developed to the other can be harnessed to counteract rapid development of multi-drug resistance.
Following up on this body of work, our iGEM team asked the following question: Can we artificially engineer a bacterial strain that would lead to selection against antibiotic resistance in a bacterial population? In other words, given the existence of 'selection against antibiotic resistance', can we reverse-engineer a system to recapitulate that specific fitness regime?
Goals
By conferring selective advantage on a bacterial population, we intend to artificially create changes in the evolutionary fitness landscape so that bacteria harboring antibiotic resistance are out-competed. We will take advantage of the following:
1. Antibiotic as a signaling molecule
2. Differential signals to resistant and sensitive bacteria
3. 'Immunity' of bacterial strain to lambda phage infection
4. Correlation of sensitivity to antibiotic concentration with lysis versus lysogeny decision in phage infected bacteria.
Experimental System and Circuit Design
In order to set the stage for playing evolutionary competition games, we first engineer a bacterial population consisting of E. coli cells that are either sensitive or resistant to the application of the antibiotic tetracycline. Our goal is to make tetracycline sensitive cells more fit than tetracycline resistant cells. The ability to survive increasing concentrations of tetracycline is used as a measure of fitness. This idea is summarized in the Figures A and B:
MIC: The lowest concentration of an antimicrobial that will inhibit the visible growth of a microorganism after overnight incubation. Minimum inhibitory concentrations are important in laboratory culture conditions to confirm resistance of microorganisms to an antimicrobial agent and to monitor the activity of new antimicrobial agents.
A bacterial cell infected with bacteriophage lambda regulates the lysis versus lysogeny choice by modulating the amount of lambda repressor produced. High lambda repressor downregulates phage genes and concurrently upregulated its own genes that allow it to remain in lysogeny. However, the lysis pathway switch is flipped on upon decrease of lambda repressor. This is brought about by induction by exposure to UV, which causes an increase of Cro protein. It follows that increased immunity to lambda can be induced by increasing concentration of the lambda repressor, allowing the bacteria to remain in lysogeny. We simultaneously couple the lytic-lysogeny switch to tetracycline induced transcription of lambda repressor as well as tetracycline induced antibiotic resistance to comparison of fitness between resistant and sensitive cells. By this coupling, we want to tune the parameters in our system so that we land in a fitness regime that will confer selective advantage to the tetracycline sensitive cells, simultaneously selecting againt tetracycline resistant cells. This idea is summarized in Figure D:
Basic Circuit Design - The general strategy for linking lysis to tetracycline resistance involves putting a lambda transcription factor (CI) under control of the Tet promoter. This circuit causes the amount of CI in a cell to be proportional to the amount of tetracycline in the cell. Cells with higher concentrations of tetracycline have higher levels of CI, thus preventing lysis of the cell via phage. Cells with lower levels of tetracycline (cells that are resistant to tetracycline) will have less CI present and thus be more susceptible to lysis by phage.
We designed the circuit keeping in mind the following goals:
- A circuit with existing BioBricks requiring few ligations to construct
- A design that could be used with multiple types of resistance
- A robust circuit that will remain stable for large numbers of generations
- A circuit that can propagate through bacterial populations, e.g., practical for treating environmental problems.
Antibiotic Selection - The antibiotic resistance we will be selecting against in this circuit will be tetracycline. Tetracycline was selected because the Tn10 tetracycline resistance transposon has been extremely well characterized and can be activated by a non-antibiotic molecule anhydrotetracycline (ATc) that binds to the TetR transcription factor, allowing us to use a variety of approaches when characterizing the genetic circuit. TetA, the tetracycline efflux pump coded for by Tn10, is toxic to cells. As a result, under conditions of low or no tetracyline, the tetracycline sensitive cells will already have a slight advantage over the tetracycline resistant cells, which will reduce the amount of tuning required for this circuit. Furthermore, the human body is extremely tolerant of tetracycline, making it a good target for resistance reduction.
Strain Selection – To compare the relative fitness of tetracycline resistant cells versus that of tetracycline sensitive phage infected cells, we selected two strains of E. coli genotypically identical with the exception that one has the Tn10 tetracyline resistance transposon. GNB824 (tetracycline resistant) is a derivative GNB8385K (tetracycline sensitive) that had the Tn10 transposon incorporated genomically. Tn10 incorporation was screened for by assaying loss of regulation of the lysine decarboxylase loci, resulting in pH independent production of lysine decarboxylase (cells with properly incorporated transposon turn red on MacConkey agar). These nearly identical strains will allow us to assess the impact of tetracycline resistance on relative fitness.
Bacteriophage Selection - When selecting the bacteriophage to be used in this circuit, we desired a phage whose life cycle and genome had been well characterized. Bacteriophage lambda has all of this characteristics as well as the benefit of being commonly used as a cloning vector. Specifically, the lambda strain we selected can be induced to undergo lytic growth by growing lysogenic cells at 42°C. Also, due to the infectious nature of bacteriophage lambda, we selected a strain that is unable to lyse cells (amber mutation prevents the expression of lytic enzyme, protecting other bacteria within the lab from phage infection). Though the phage will not lyse the cells, it will produce fully functional phage particles that can be isolated via chloroform extraction.
Phage Engineering – We will construct a recombination plasmid designed to integrate our circuit into lambda DNA located chromosomally in lysogen E. coli. The plasmid will not contain an origin of replication (to limit recombination sites), so we will have to amplify it using high fidelity PCR. The plasmid will contain our circuit flanked by homologous recombination sites that will combine at a non-critical location of the phage chromosome (yet to be determined). Within this homologous recombination site, we will construct a BioBrick restriction site, allowing us to integrate any BioBrick part into the lambda phage genome.
Circuit Characterization – To assay relative fitness of the cells, we will measure doubling times of the strains at sub-MIC tetracycline by measuring optical density (600nm) of cells.
Experimental Materials and Methods
The overall construction scheme with the modular parts of the circuit is shown in Figure C. Differential response to exposure to tetracycline is schematized in Figure D. Biobrick parts used in the circuit are shown in Figure E.
Testing and Characterization of the Constructed Circuit
Using promoters of different strengths, the circuit has been characterized for its ability to grow in various concentrations of tetracycline. The EYFP fluorescent reporter serves as a readout for the functionality of the circuit as a Tet sensor. The Lambda Generator part is described in Figure F. The final circuit is presented below, in Figure G.
Constructs Submitted and Verified
Modeling
We use stochastic differential equations to represent chemical reactions with each reacting species being a component of the circuit. Numerical solutions are obtained by the Gillespie Stochastic Simulation Algorithm, implemented in Matlab. Here is the code used. Figure H shows the reactions used in the modeling.
The Gillespie algorithm is used to perform a discrete stochastic simulation of a system of well mixed reactant molecules wherein the 'fate trajectory' of each molecule is explicitly simulated. A Gillespie simulation is a random walk that exactly represents the distribution of the Chemical Master Equation. The physical interpretation of the Simulation is that individual molecules participating as reactants in a system undergo frequent collisions, a sub-set of which are collisions that are in correct stereo-chemical orientation and with sufficient potential energy. In a Gillespie Simulation exercise, a well mixed reaction environment is presumed. Each of the participating species is explicitly traced so that (a) which reaction will occur at the next time step and (b) the probability of a reaction occurring at the next time step is known. The Gillespie method of stochastic simulation is advantageous over the deterministic differential equation based modeling of chemical reactions assuming mass action kinetics because it does not approximate chemical reactions as occurring in bulk but rather accounts for a chemical reaction occurring between two chemical species.
The following assumptions are made:
- Any spatial aspects of the modeling problem are ignored (i.e. Gillespie is only running in time)
- Parameter values are input from the following references:
- Hooshangi, S. Thiberge, S., Wiess R. Ultra sensitivity and Noise Propagation in Synthetic Transcriptional Cascade. PNAS 2005; 102(10). pp. 3351-3586
- Sotiropoulos, V. and Kaznessis, Y. N. Synthetic tetracycline-inducible regulatory networks: computer-aided design of dynamic phenotypes. BMC Systems Biology. Jan 2009.
- Steps in gene expression (i.e. transcription and translation) are simplified by not modeling RNAP binding/unbinding to the promoter and Ribsome binding/unbinding; modified propensities are used from the reference above.
- Growth rates are assumed not to vary among cell types (i.e. infected vs. non-infected).
- Initial concentrations are assumed not to be different among different cell types.
- The propensities for tetA is recovered from experimental data in the literature.
For the circuit constructed, one of the possible readouts of 'measure of fitness' in the wake of tetracycline exposure would be the amount of CI produced. Through the simulations, we trace the time evolution profiles of CI production and compare the results in Tet-sensitive and Tet-resistant cells. We infer that the probability of a population of Tet-resistant E. coli cells going into lysis over the choice to remain in lysogenic state increases after tetracycline challenge.
Results
Predictive Modeling of the Circuit
The modeling exercise provided us with a proof-of-principle that it should be possible to engineer production of lambda repressor under the control of Tetracycline such that Tetracycline resistant cells are under a fitness disadvantage regime and are out competed by the Tetracycline sensitive cells. From this model, we intend to extract the follwing information:
- Concentration profile of Tetracycline necessary for induction of the circuit.
- The probability of lysis given a specific induction of the circuit by tetracycline.
The modeling exercise provided us a proof of principle that it should be possible to engineer production of lambda repressor under the control of tetracycline such that tetracycline resistant cells are under a fitness disadvantage regime and are out competed by the tetracycline sensitive cells (Figure I).
Before, the full scale simulation was run, preliminary models were run in order to better understand the results of the different plasmid constructs. These experimental results helped to fine tune the parameters of the model. This refined model could then predict the dynamic of the engineered circuit within the phage genome in order to understand the effects of stochasticity and gene copy number on the efficacy of the circuit's ability to decrease the fitness of resistant cells (Figure J).
In the early stages of designed the circuit, the negative feedback on TetR expression was added in order to decease the noise in the circuit and to provide more stable expression levels of TetR for varying gene copy numbers as predicted by the preliminary model.
Later, we used the model to analyze the effects of altering the strength of cI repression by TetR as well as the negative feedback of TetR.
Characterization of the Circuit
The doubling times listed in the table to the left provide the relative fitness of TetS and TetR cells grown at different temperatures containing different circuits. The data indicate that, at 37 degrees C, our circuit does not impact the doubling time of TetR or TetS cells.
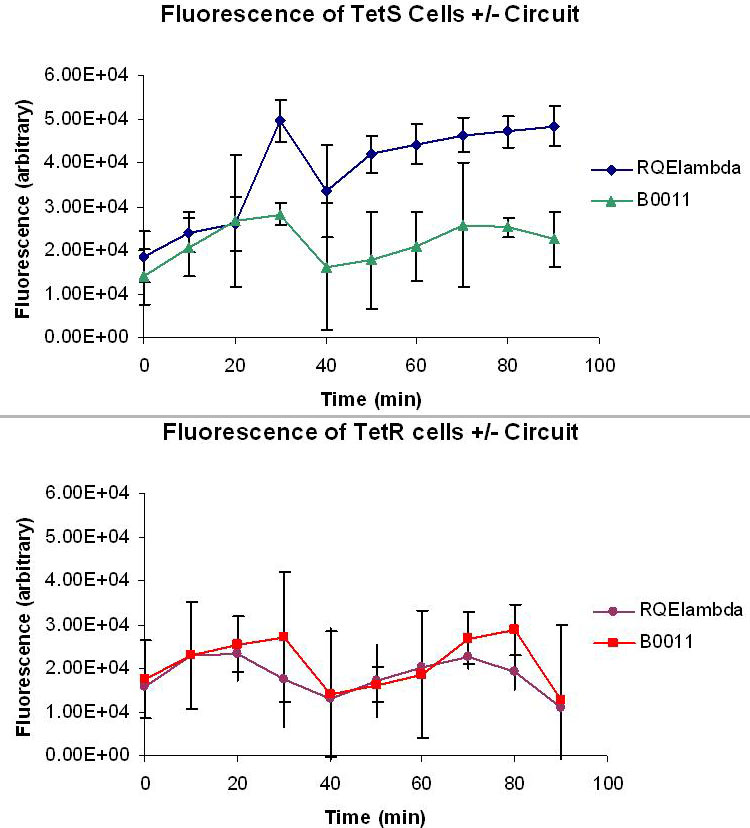
Figure K and L measures the relative fluorescence of TetR and TetS cells with and without our circuit. The cells were cultured at 37 degrees C in M9 minimal media with 50ug/mL ampicillin and 1uM ATc. 1uM ATc is assumed to fully induce our circuit and produce a bolus of EYFP and CI in both TetS and TetR cells. The effectiveness of our circuit will be determined by the ratio of the fluorescence produced by TetS TetR. A high TetS/TetR ratio indicates that TetS cells are producing much more CI than the TetR cells, making any TetS lysogen much less likely to go into lytic phase. The data show that the fluorescence levels of TetR+RQEλ55 + are negligible when compared to the autofluorescence of TetR+B0011 while TetS+RQEλ55 produces a noticeable amount of fluorescence when compared to the TetS+B0011. At 100% induction, it appears that our circuit it binary. TetS+RQEλ55 cells will produce EYFP and CI while TetR+RQEλ55 produce almost no EYFP and CI.
Milestones Accomplished
Watch out for our presentation and poster at the Jamboree!