Davidson Missouri W/WesternMeetingNotes

From 2007.igem.org

< Davidson Missouri W(Difference between revisions)
(→Western Meeting Notes)
 
(10 intermediate revisions not shown)
Line 1: Line 1:
-
===Western Meeting Notes===
+
===Western Meeting Notes===
 +
   
 +
'''5/14 Overview of goals for the next two weeks'''
-
'''6/04 Original Adelman Graph'''
+
Begin Experimentation
 +
 +
Educational Information 
 +
 +
Literature Research 
 +
-
[[Image:AdelmanGraph.JPG|thumb|300px|center| ]]
+
'''5/15''' 
-
<br>
+
-
The Adelman Graph with its seven vertices and fourteen arcs is too large to attack with our approach without first testing our procedures.  To this end, Michelle and Jeff have been investigating induced subgraphs of the Adelman Graph.  Ideally, we would like to partition the Adelman Graph into smaller graphs that could be constructed and tested individually, then linked together to form one large construct representing the Adelman Graph. It seems the most critical property of a good test graph is a unique Hamiltonian path. The smallest graph with a unique Hamiltonian path would be two vertices connected with a single edge. This is the one pancake problem worked on (and successfully achieved!) by the Davidson-Missouri Western team in 2006.  The first non-trival (from a mathematical standpoint) graph would be a transitive directed graph on three vertices. The concept of transitivity is pervasive in many areas of mathematics.  In the real numbers, the relation > is transitive.  That is, if a>b and b>c, then we know that a>c.  One example of a transitive induced graph of the Adelman graph is the subgraph on the vertices 1, 4, and 2.  Notice that the edges of the Adelman Graph between these three vertices are precisely 14, 42, and 12.  This construct, and others like it, have a unique Hamiltonian path AND have the property that there are no false positive results.  This may provide a setting in which to test some of our proposed procedures.
+
Reviewed PowerPoint presentations of 2006 project to gain an understanding of the Pancake Problem.   
 +
Viewed Bruce's presentation on the mutation of the hix sites  
 +
 +
Developed plan to build testing constructs of mutant hix sites, arriving this afternoon from Davidson by FedEx  
 +
   
 +
Will build pLac - hix(n) - BBa_S03644 (RFPrev-RBSrev) - hix(n) on AmpR plasmid. Details to follow.   
-
'''6/11 Adelman Subgraph'''
+
'''Note -- The above plan has changed as of Tuesday afternoon because of availability of parts.'''
-
Moving up a level, the graph below is nearly an induced subgraph of the Adelman Graph.  (To be induced, it would require the arc 27 also be included, but to include this edge would destroy the property of having a unique Hamiltonian path.) This graph on four vertices with six edges provides a small example in which we can test our ability to biologically distinguish between true positives and false positives. There are 48 true positives for this graph (14, 47, 72 followed by the other three arcs in any order and any orientation).  There are 42 false positives (14, 47, 74 followed by the other three arcs in any order but with at least one in forward orientation).
+
BBa_S03644 is not available in our lab and the exact forward equivalent appears (amazingly) to not exist anywhere. However, there is an RBS - RFP in the Registry (BBa_I13502) which is a preassembled combination of a weaker RBS (BBa_B0034) and RFP (BBa_E1010). There is also a full positive control assembly (BBa_J04450) of pLac - B0034 - E1010 - Term. We will need to be careful to use the same parts in our Hix(n) assemblies so that we can test for only the functionality of our construct with the mutated Hix sites included.
-
[[Image:HamiltonInduced4.JPG|thumb|300px|center| ]]
+
'''5/16''' 
-
<br>
+
-
The graph below is an induced subgraph of the Adelman Graph on five vertices with nine arcs. This graph has a unique Hamiltonian path AND contains the graph above.  This might serve as a good intermediate on our way to the complete construction.  Note also that this graph contains three transitive subgraphs (7,4,2), (4,7,2) and (1,4,2).  Before jumping into constructions, we should carefully consider which coding sequence will correspond to each vertex of the Adelman Graph.  If we are clever, it may be possible to piece together several smaller test constructs to efficiently create the full graph.  Note:  The counting of true positives and false positives for the graph below is non-trivial and in progress.
+
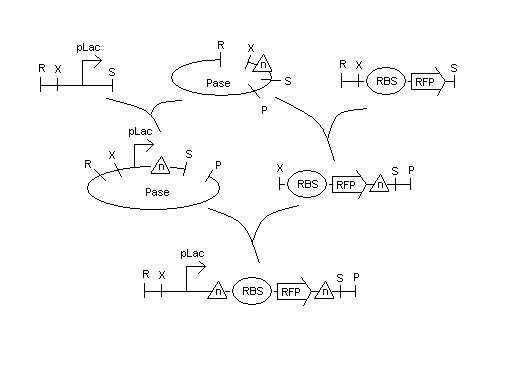
We have cultures that were grown overnight of the Hix(n). We received the sequencing data on the Karen's and Bruce's Hix(n) constructs (from 5/14 report) and are analyzing the data to find the mutations. Lab work continues.   
-
[[Image:HamiltonInduced5.JPG|thumb|300px|center| ]]
+
[[Image:hixn.jpg|thumb|500px|center| ]]
-
<br>
+
-
'''6/13 One Time Flipable Investigation'''
+
'''5/17'''
 +
 +
Karen developed a modified Green Fuorescent protein, GFP, by splitting the DNA for GFP, reversing one portion and adding Hix sites to it. This way, GFP can only be produced when the reversed portion is inverted so that the entire gene is in the correct order. This method was attempted with the TET resistance gene with no results. We have looked at using several fluorescent proteins modified in this manner to study the Traveling Salesman. In this manner, the proteins would only be expressed if they had all been lined up in the correct order. This approach has some flaws however, all fluorescent proteins are similar in structure, so that even if the portions of two different genes come together, the resulting protein may still fluoresce. Additionally, fluorescent protiens have the ability to undergo fluorescent resonant energy transfer, FRET, a phenomenon in which energy absorbed by one molecule is directly transfered to a second molecule, this prevents the first molecule from emitting visible photons, so that it may remain undetected. 
 +
 +
'''5/21''' 
 +
 
 +
Students -- For this week and the first half of next, we will not be doing labwork as Dr. Eckdahl will be out of town until next Thursday afternoon. In the meantime, we can be investigating the two literature questions below. Please look for pertinent articles and include notes and references on the main WIKI page when you find something good. Our two questions are: 
 +
 
 +
 +
1. Can one promoter drive more than one coding sequence on a plasmid in bacteria? (i.e., Do polycistronic systems function one plasmids in bacteria?)
 +
 
 +
2. What promoters are available in the Registry or are known from the literature that we can control (either by inducing or repressing)?
-
[[Image:onetimeflipable.JPG|thumb|600px|center| ]]
+
Feel free to communicate via e-mail with Drs. Eckdahl and Poet as you find things. Be sure to document what you find as you find it so we can move forward as a team and not spend time duplicating our efforts. 
-
<br>
+
 +
'''5/23'''
 +
Missouri Governor Matt Blunt came to campus today to sign an important piece of legislation providing funding for a 60,000 square foot addition to Agenstein Hall, Missouri Western's mathematics and science building and providing need-based scholarships for more students from Missouri. Governor Blunt addressed a standing room only crowd in Agenstein Room 205 and was accompanied by several state legislators including Shields, Schaaf, and Rucker. One MWSU student was asked to make comments while the governor signed the bill. That student was Davidson - Missouri Western iGEM team member Jordan Baumgardner. Jordan did a great job. Team member Tom Crowley and team co-leader Jeff Poet attended the signing ceremony as did 2006 team member Marian Broderick. This may be the first official plug for our 2007 team. Way to go!
 +
 
 +
'''6/6'''
 +
 
 +
Jeff and Michelle (and Matt as a bystander) had a conference call with Laurie, Phillip, Jim, and Amber regarding the "math side of things". The Davidson crew has been working full-time for a little over a week now on several projects. Phillip has been looking at the existence of cycles of various lengths in Pancake graphs and Burnt Pancake graphs and has come up with several conjectures. (As I understand, the conjectures have been shown to be true up to the capacity limits of MATLAB regarding the size of the adjacency matrices. Maybe?) Phillip has been writing MATLAB code to look for 3-,4-,5-, and 7-cycles in the different graphs. He may be sending the code for us to review here and to try it on our machines as the need warrants. Jim and Amber have been working with Markov chains, using ideas from Phillip's programs to build models with varying probabilities relating to the likelihood of flipping a single pancake or doubled pancake in the 3 burnt pancake model. They have considered both the mathematical idea of independence of the stacks and the idea of biologically equivalent stacks. That is, treating 1,2 as different than -2,-1 and also treating the two as the same. In relation to the HPP, the Davidson crew has been trying to count the probability of generating a false positive result from Adelman's graph on seven vertices with twelve edges. For reference, we will use the following notation throughout the project (or until further notice anyway). The Davidson biology crew is particularly interested in the magnitude of the number of false positives in relation to a true HPP before proceeding to build something with little chance of giving a nice result.
 +
 +
 +
On the Western side of things, we have been looking at induced subgraphs of the Adelman graph with the idea of finding smaller testable constructs that can be linked to produce the full Adelman graph. The hope is to aid in the development of the construction plan for the biology side of the team. On the technology front, we await the anticipated arrival of the iMac computer sometime this week. With a measure of luck, we will be able to videoconference late next week!
 +
 
 +
The tentative plan of attack for Michelle and Jeff is to work on the following things:
 +
 
 +
1. Look at the MATLAB graphs from the Davidson crew with the idea of potentially morphing them into something more visually appealing. (Regular, degree-6, planar graph on 48 vertices but produced with only straight lines. Perhaps moving vertices or allowing a few curved edges will make the graph more user-friendly. 
 +
 
 +
2. Work on counting the false positives possible using only the edges of the Adelman graph, to assist the Davidson crew or to confirm their result. Ideally, we would reach the same result by more than one method. 
 +
 +
3. While not talked about in the conference call, we plan to investigate the math behind some of the implications of one-time flippable hix sites. It seems that there may be some interesting and unexpected thigns going on there that we may need to look into before we get surprised.
 +
 
 +
This will be enough to keep us busy for some time. It was great to touch bases with the Davidson crew and to introduce ourselves. We look forward to a video introduction next week. JLP 
 +
 
 +
'''6/7'''
 +
 +
A method of stopping Hix site flipping by destroying the Hin recombinase DNA with restriction enzymes was devised. A search was done to determine what restriction enymes would cut the DNA sequence, then the results were filtered to find an enzyme with a 6 base pair cutting site, and cut the DNA in at least two places. This yielded two results: 
 +
 
 +
 +
    BmrI 5'...ACTGGG(N)5^...3' 
 +
          3'...TGACCC(N)4^...5' 
 +
 
 +
    NmeAIII 5'...GCCGAG(N)21^...3'
 +
            3'...CGGCTC(N)19^...5' 
 +
 
 +
The ^ is where the enzyme cuts. Those numbers after the parentheses should be subscripted.
 +
 
 +
'''7/6'''
 +
 
 +
The phenotypes of several clones were tested by smearing some bacteria from each clone on plates containing either  Kan, Amp, or Tet antibiotics. Results are as follows
 +
 
 +
    Clone    Kan    Amp    Tet
 +
    13502    Dies    Lives  Dies
 +
    21 1A7    Dies    Lives  Dies
 +
    21 1A2    Lives  Lives  Lives
 +
    09        Lives  Lives  Lives
 +
    10        Dies    Lives  Dies
 +
    11        Lives  Lives  Lives
 +
    30        Dies    Lives  Dies

Latest revision as of 17:51, 6 July 2007

Western Meeting Notes

5/14 Overview of goals for the next two weeks

Begin Experimentation

Educational Information

Literature Research


5/15

Reviewed PowerPoint presentations of 2006 project to gain an understanding of the Pancake Problem. Viewed Bruce's presentation on the mutation of the hix sites

Developed plan to build testing constructs of mutant hix sites, arriving this afternoon from Davidson by FedEx

Will build pLac - hix(n) - BBa_S03644 (RFPrev-RBSrev) - hix(n) on AmpR plasmid. Details to follow.

Note -- The above plan has changed as of Tuesday afternoon because of availability of parts.

BBa_S03644 is not available in our lab and the exact forward equivalent appears (amazingly) to not exist anywhere. However, there is an RBS - RFP in the Registry (BBa_I13502) which is a preassembled combination of a weaker RBS (BBa_B0034) and RFP (BBa_E1010). There is also a full positive control assembly (BBa_J04450) of pLac - B0034 - E1010 - Term. We will need to be careful to use the same parts in our Hix(n) assemblies so that we can test for only the functionality of our construct with the mutated Hix sites included.

5/16

We have cultures that were grown overnight of the Hix(n). We received the sequencing data on the Karen's and Bruce's Hix(n) constructs (from 5/14 report) and are analyzing the data to find the mutations. Lab work continues.

Hixn.jpg

5/17

Karen developed a modified Green Fuorescent protein, GFP, by splitting the DNA for GFP, reversing one portion and adding Hix sites to it. This way, GFP can only be produced when the reversed portion is inverted so that the entire gene is in the correct order. This method was attempted with the TET resistance gene with no results. We have looked at using several fluorescent proteins modified in this manner to study the Traveling Salesman. In this manner, the proteins would only be expressed if they had all been lined up in the correct order. This approach has some flaws however, all fluorescent proteins are similar in structure, so that even if the portions of two different genes come together, the resulting protein may still fluoresce. Additionally, fluorescent protiens have the ability to undergo fluorescent resonant energy transfer, FRET, a phenomenon in which energy absorbed by one molecule is directly transfered to a second molecule, this prevents the first molecule from emitting visible photons, so that it may remain undetected.

5/21

Students -- For this week and the first half of next, we will not be doing labwork as Dr. Eckdahl will be out of town until next Thursday afternoon. In the meantime, we can be investigating the two literature questions below. Please look for pertinent articles and include notes and references on the main WIKI page when you find something good. Our two questions are:


1. Can one promoter drive more than one coding sequence on a plasmid in bacteria? (i.e., Do polycistronic systems function one plasmids in bacteria?)

2. What promoters are available in the Registry or are known from the literature that we can control (either by inducing or repressing)?

Feel free to communicate via e-mail with Drs. Eckdahl and Poet as you find things. Be sure to document what you find as you find it so we can move forward as a team and not spend time duplicating our efforts.

5/23 Missouri Governor Matt Blunt came to campus today to sign an important piece of legislation providing funding for a 60,000 square foot addition to Agenstein Hall, Missouri Western's mathematics and science building and providing need-based scholarships for more students from Missouri. Governor Blunt addressed a standing room only crowd in Agenstein Room 205 and was accompanied by several state legislators including Shields, Schaaf, and Rucker. One MWSU student was asked to make comments while the governor signed the bill. That student was Davidson - Missouri Western iGEM team member Jordan Baumgardner. Jordan did a great job. Team member Tom Crowley and team co-leader Jeff Poet attended the signing ceremony as did 2006 team member Marian Broderick. This may be the first official plug for our 2007 team. Way to go!

6/6

Jeff and Michelle (and Matt as a bystander) had a conference call with Laurie, Phillip, Jim, and Amber regarding the "math side of things". The Davidson crew has been working full-time for a little over a week now on several projects. Phillip has been looking at the existence of cycles of various lengths in Pancake graphs and Burnt Pancake graphs and has come up with several conjectures. (As I understand, the conjectures have been shown to be true up to the capacity limits of MATLAB regarding the size of the adjacency matrices. Maybe?) Phillip has been writing MATLAB code to look for 3-,4-,5-, and 7-cycles in the different graphs. He may be sending the code for us to review here and to try it on our machines as the need warrants. Jim and Amber have been working with Markov chains, using ideas from Phillip's programs to build models with varying probabilities relating to the likelihood of flipping a single pancake or doubled pancake in the 3 burnt pancake model. They have considered both the mathematical idea of independence of the stacks and the idea of biologically equivalent stacks. That is, treating 1,2 as different than -2,-1 and also treating the two as the same. In relation to the HPP, the Davidson crew has been trying to count the probability of generating a false positive result from Adelman's graph on seven vertices with twelve edges. For reference, we will use the following notation throughout the project (or until further notice anyway). The Davidson biology crew is particularly interested in the magnitude of the number of false positives in relation to a true HPP before proceeding to build something with little chance of giving a nice result.


On the Western side of things, we have been looking at induced subgraphs of the Adelman graph with the idea of finding smaller testable constructs that can be linked to produce the full Adelman graph. The hope is to aid in the development of the construction plan for the biology side of the team. On the technology front, we await the anticipated arrival of the iMac computer sometime this week. With a measure of luck, we will be able to videoconference late next week!

The tentative plan of attack for Michelle and Jeff is to work on the following things:

1. Look at the MATLAB graphs from the Davidson crew with the idea of potentially morphing them into something more visually appealing. (Regular, degree-6, planar graph on 48 vertices but produced with only straight lines. Perhaps moving vertices or allowing a few curved edges will make the graph more user-friendly.

2. Work on counting the false positives possible using only the edges of the Adelman graph, to assist the Davidson crew or to confirm their result. Ideally, we would reach the same result by more than one method.

3. While not talked about in the conference call, we plan to investigate the math behind some of the implications of one-time flippable hix sites. It seems that there may be some interesting and unexpected thigns going on there that we may need to look into before we get surprised.

This will be enough to keep us busy for some time. It was great to touch bases with the Davidson crew and to introduce ourselves. We look forward to a video introduction next week. JLP

6/7

A method of stopping Hix site flipping by destroying the Hin recombinase DNA with restriction enzymes was devised. A search was done to determine what restriction enymes would cut the DNA sequence, then the results were filtered to find an enzyme with a 6 base pair cutting site, and cut the DNA in at least two places. This yielded two results: 


    BmrI 5'...ACTGGG(N)5^...3'   
         3'...TGACCC(N)4^...5'   

    NmeAIII 5'...GCCGAG(N)21^...3' 
            3'...CGGCTC(N)19^...5'

The ^ is where the enzyme cuts. Those numbers after the parentheses should be subscripted.

7/6

The phenotypes of several clones were tested by smearing some bacteria from each clone on plates containing either Kan, Amp, or Tet antibiotics. Results are as follows 

    Clone     Kan     Amp     Tet
    13502     Dies    Lives   Dies
    21 1A7    Dies    Lives   Dies
    21 1A2    Lives   Lives   Lives
    09        Lives   Lives   Lives
    10        Dies    Lives   Dies
    11        Lives   Lives   Lives
    30        Dies    Lives   Dies
Retrieved from "http://2007.igem.org/wiki/index.php/Davidson_Missouri_W/WesternMeetingNotes"