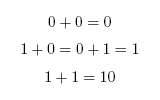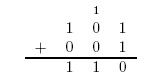Project
From 2007.igem.org
(→Logic Gates and Implementing an Adder) |
(→Molecular Mechanism) |
||
| (26 intermediate revisions not shown) | |||
| Line 40: | Line 40: | ||
When working in binary, only two digits are used: 0 and 1. A single binary digit is called a '''bit'''. Counting proceeds as: | When working in binary, only two digits are used: 0 and 1. A single binary digit is called a '''bit'''. Counting proceeds as: | ||
To add two binary numbers, the process is much the same as adding two decimal (ordinary) numbers, except that instead of carrying when two digits add to ten, carrying must be performed when two digits add to two. In other words, 0 + 1 adds to 1, but 1 + 1 adds to 0 with a carry of 1, which gives 10 (just as in decimal 1 + 9 would add to 0 with a carry of 1, to give 10). A complete list of the possibilities is as follows: | To add two binary numbers, the process is much the same as adding two decimal (ordinary) numbers, except that instead of carrying when two digits add to ten, carrying must be performed when two digits add to two. In other words, 0 + 1 adds to 1, but 1 + 1 adds to 0 with a carry of 1, which gives 10 (just as in decimal 1 + 9 would add to 0 with a carry of 1, to give 10). A complete list of the possibilities is as follows: | ||
| + | |||
| + | [[Image:000.jpg]] | ||
Here is an example of long addition: | Here is an example of long addition: | ||
<div style="float:center;width:225px;"> | <div style="float:center;width:225px;"> | ||
| - | + | [[Image:222.jpg]]<br clear="all" /> | |
</div> | </div> | ||
| Line 73: | Line 75: | ||
For the following explanations, A and B represent statements that can be either true or false. | For the following explanations, A and B represent statements that can be either true or false. | ||
| - | <table | + | <center><table cols="3" style="border: 1px solid gray; border-collapse: collapse; padding:15px; "> |
<tr style="background-color:#CCCCCC; text-align:left;"> | <tr style="background-color:#CCCCCC; text-align:left;"> | ||
| - | < | + | <th>Operator</th> |
| - | < | + | <th>Condition </th> |
| - | < | + | <th>Truth Table</th> |
</tr> | </tr> | ||
| - | <tr valign="middle" style="border-top: 1px solid | + | <tr valign="middle" style="border-top: 1px solid gray;border-bottom: 1px solid gray;"> |
| - | <td>a OR b</td> | + | <td style="padding:2em;">a OR b</td> |
| - | <td>If a, b, or both are true</td> | + | <td style="padding:2em;">If a, b, or both are true</td> |
<td>[[Image:UW_Or_TABLE.jpg]]</td> | <td>[[Image:UW_Or_TABLE.jpg]]</td> | ||
</tr> | </tr> | ||
| - | <tr valign="middle" style="border-top: 1px solid | + | <tr valign="middle" style="border-top: 1px solid gray;border-bottom: 1px solid gray;"> |
| - | <td>a XOR b</td> | + | <td style="padding:2em;">a XOR b</td> |
| - | <td>If a and b are different</td> | + | <td style="padding:2em;">If a and b are different</td> |
<td>[[Image:UW_XOR_TABLE.jpg]]</td> | <td>[[Image:UW_XOR_TABLE.jpg]]</td> | ||
</tr> | </tr> | ||
| - | <tr valign="middle" style="border-top: 1px solid | + | <tr valign="middle" style="border-top: 1px solid gray;border-bottom: 1px solid grayk;"> |
| - | <td>AND</td> | + | <td style="padding:2em;">AND</td> |
| - | <td>If both are true</td> | + | <td style="padding:2em;">If both are true</td> |
<td>[[Image:UW_And_TABLE.jpg]]</td> | <td>[[Image:UW_And_TABLE.jpg]]</td> | ||
</tr> | </tr> | ||
| - | <tr valign="middle" style="border-top: 1px solid | + | <tr valign="middle" style="border-top: 1px solid gray;"> |
| - | <td>NOT a</td> | + | <td style="padding:2em;">NOT a</td> |
| - | <td>If a is false</td> | + | <td style="padding:2em;">If a is false</td> |
<td>[[Image:UW_NOT_TABLE.jpg]]</td> | <td>[[Image:UW_NOT_TABLE.jpg]]</td> | ||
</tr> | </tr> | ||
| - | </table> | + | </table></center> |
| Line 107: | Line 109: | ||
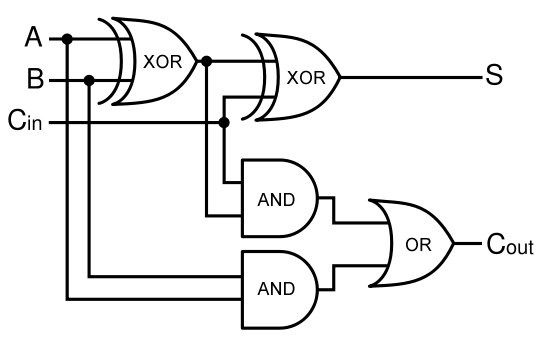
Given two binary inputs A and B, their sum can be computed by passing these inputs through various logic gates. The process is illustrated in Figures 4 and 5. | Given two binary inputs A and B, their sum can be computed by passing these inputs through various logic gates. The process is illustrated in Figures 4 and 5. | ||
| - | < | + | <table style="border-width:0px:vertical-align:middle;width:100%"> |
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Half-adder.png|left|thumb|300px|Figure 4: Half-adder circuit diagram]] | ||
| + | </td> | ||
| + | <td> | ||
| + | [[Image:Full-adder.png|left|thumb|300px|Figure 5: Full-adder circuit diagram]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br clear="all" /> | ||
===DNA as Logic Gates=== | ===DNA as Logic Gates=== | ||
Our project focuses on using DNA as logic gates. The output of a logical operation is the protein product of a certain gene; the inputs are external stimuli that cause allosteric changes in the conformation of proteins that can induce or inhibit transcription by acting on promoter elements. Whether or not the gene is turned 'on' or 'off' depends on the logic gate implemented. | Our project focuses on using DNA as logic gates. The output of a logical operation is the protein product of a certain gene; the inputs are external stimuli that cause allosteric changes in the conformation of proteins that can induce or inhibit transcription by acting on promoter elements. Whether or not the gene is turned 'on' or 'off' depends on the logic gate implemented. | ||
| - | For | + | For two inputs, the "presence" or "absence" of input A and the "presence" or "absence" of protein B (both representing 0 or 1 as inputs) would result in an output of either the "presence" or "absence" of protein X (where "presence" and "absence" should be read as high and low intensity/concentration, respectively). |
| - | + | For example, consider a regulated gene G that codes for protein X. By default, the gene is not expressed (to be precise, there is a low basal level of expression that we can disregard). If the inputs A and B are on and together can turn on expression of gene G, the expressed protein X represents the output of an AND gate. This is the type of approach used to construct our biological adder. | |
| - | + | ||
| - | This is the type of approach used to construct our biological adder | + | |
==Project Details== | ==Project Details== | ||
| - | + | ===Input and Output=== | |
| + | |||
| + | <table style="border-width:0px;width:100%;vertical-align:text-bottom"> | ||
| + | <tr> | ||
| + | <td> | ||
| - | |||
As a half-adder, our device requires two binary inputs; the possible 1 and 0 values of these inputs are represented by the presence and absence of two stimuli. For the first input, the presence of red light represents a 0 and the absence represents a 1. For the second input, the absence of tetracycline represents a 0 and the presence represents a 1. | As a half-adder, our device requires two binary inputs; the possible 1 and 0 values of these inputs are represented by the presence and absence of two stimuli. For the first input, the presence of red light represents a 0 and the absence represents a 1. For the second input, the absence of tetracycline represents a 0 and the presence represents a 1. | ||
| Line 131: | Line 144: | ||
Depending on the result of the calculation, the bacteria will produce either red fluorescent protein (RFP), green fluorescent protein (GFP), or neither. A diagram of the biological half adder in culture is shown above, depicting the possible outcomes for each combination of inputs. | Depending on the result of the calculation, the bacteria will produce either red fluorescent protein (RFP), green fluorescent protein (GFP), or neither. A diagram of the biological half adder in culture is shown above, depicting the possible outcomes for each combination of inputs. | ||
| + | </td> | ||
| + | <td> | ||
| + | [[Image:UW_biology_schematic_diagram.PNG|none|thumbnail|center|500px|Inputs and Output of the Biological Half-Adder]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | ===Molecular Mechanism=== | ||
| + | |||
| + | As components of a natural quorum sensing system, LuxR and LuxI proteins are ideal for producing the AND logic function required to create 1-bit half-adder. LuxR enhances transcription at Plux when activated by an inducer produced by LuxI. The expression of both LuxR and LuxI is therefore necessary to "turn on" the promoter Plux. LasR and LasI have analogous roles in another quorum sensing system, and contribute to the XOR logic function in our design. Below is a diagram showing all of the gene constructs that are involved in the biological half adder (these will ultimately be included on a single plasmid, but are here shown separately for ease of explanation). | ||
| - | |||
[[Image:GeneDesignHA.jpg|none|thumbnail|center|500px|Gene Diagram for the Half Adder Construction]] | [[Image:GeneDesignHA.jpg|none|thumbnail|center|500px|Gene Diagram for the Half Adder Construction]] | ||
| - | |||
| - | The products in the first | + | The products in the first, third, and fifth constructs are always produced while the other constructs are controlled by various proteins that either induce or inhibit the production of the proteins that these genes encode. |
| - | + | <br clear="all"> | |
| - | + | The behaviour of the half-adder can be described by four possible cases which are simulated in the genetic system as follows: | |
| - | This is achieved through the | + | <table style="border: 1px solid gray;text-align:left"> |
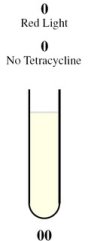
| + | <tr><td rowspan="2" style="border-bottom: 1px solid gray;padding-bottom:10px">[[Image:Tube00.jpg]]</td><th style="font-size:medium">Case 1: 0 + 0 = 0</th></tr> | ||
| + | <tr><td style="border-bottom: 1px solid gray;"> | ||
| + | This is achieved through the presence of red light and absence of tetracycline. | ||
| - | In the absence of tetracycline, the | + | In the absence of tetracycline, the TetR repressor protein that is constitutively being produced by the third construct will bind to the operator on the fourth construct preventing the production of LasR and LuxR. |
| - | In the | + | In the presence of red light, the complex formed by Cph8, Ho1, and PcyA is inactivated and thus cannot activate OmpR to act on the Pomp promoter. Without OmpR, the proteins LasR and LuxI will not be produced. |
| - | The protein | + | The protein LasR is required for the production of Green Fluroescent Protein (GFP). For Red Fluroescent Protein (RFP) to be produced, the proteins LuxI and LuxR must both be present in the cell. |
| - | In the absence of | + | In the absence of LasR, LuxI, and LuxR, neither of the reporter genes RFP or GFP will be produced. |
| - | Consequently, there will not be any output representing a result of 0 for the computation. | + | Consequently, there will not be any output (i.e., no colour produced), representing a result of 0 for the computation. |
| - | + | </td></tr> | |
| - | Case 2: 1 + 0 = 1 | + | <tr><td rowspan="2" style="border-bottom: 1px solid gray;padding-bottom:10px">[[Image:Tube10.jpg]]</td><th style="font-size:medium">Case 2: 1 + 0 = 1</th></tr> |
| + | <tr><td style="border-bottom: 1px solid gray;"> | ||
| + | This is achieved through the absence of both red light and tetracycline. | ||
| - | + | In the absence of tetracycline, the TetR repressor binds to the operator on the fourth construct preventing the production of LasR and LuxR. | |
| - | In the absence of | + | In the absence of red light, however, the components Cph8, Ho1, and PcyA will combine to form a complex to activate ompR. This complex will bind to the promoter of the second construct activating the production of the proteins LasR and LuxI. |
| - | + | Since the LasR protein is now present, it can be activated by the constitutively produced LasI to turn on the promoter of the sixth construct and induce the production of GFP. | |
| - | + | However, the presence of the LuxI protein alone is insufficient to activate the production of RFP. | |
| - | + | ||
| - | However, the presence of the | + | |
Consequently, the output is green. | Consequently, the output is green. | ||
| - | + | </td></tr> | |
| - | Case 3: 0 + 1 = 1 | + | <tr><td rowspan="2" style="border-bottom: 1px solid gray;padding-bottom:10px">[[Image:Tube01.jpg]]</td><th style="font-size:medium">Case 3: 0 + 1 = 1</th></tr> |
| - | + | <tr><td style="border-bottom: 1px solid gray;"> | |
| - | This case is similar to Case 2. This is achieved through the | + | This case is similar to Case 2. This is achieved through the presence of both red light and tetracycline. |
| - | In the | + | In the presence of red light, the proteins Cph8, Ho1, and PcyA do not activate ompR. Thus, nothing acts on the promoter in the second construct to induce the production of the LasR and LuxI proteins. |
| - | When tetracycline is present, tetracycline binds to the repressor protein | + | When tetracycline is present, tetracycline binds to the repressor protein TetR, which causes a conformational change to TetR and prevents it from binding to the operator on the fourth construct. This allows the proteins LasR and LuxR to be produced. |
| - | The | + | The LasR protein then acts on the promter of the last construct inducing the production of GFP. However, LuxR alone cannot induce the production RFP, so only GFP is produced. |
Consequently, the output is green. | Consequently, the output is green. | ||
| - | + | </td></tr> | |
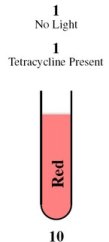
| - | Case 4: 1 + 1 = 10 | + | <tr><td rowspan="2">[[Image:Tube11.jpg]]</td><th style="font-size:medium">Case 4: 1 + 1 = 10</th></tr> |
| - | + | <tr><td> | |
| - | This is achieved through the | + | This is achieved through the absence of red light and the presence of tetracycline. |
| - | In the | + | In the absence of red light, the proteins Cph8, Ho1, and PcyA combine to form a complex that activates OmpR. This complex then binds to the promoter of the third construct and induces the production of the LasR and LuxI proteins. |
| - | In the presence of tetracycline, | + | In the presence of tetracycline, TetR undergoes a conformational change that prevents it from binding to the operator of the fourth construct. As a result, LasR and LuxR proteins are produced. |
| - | Since the proteins | + | Since the proteins LuxI and LuxR are present, they induce the production of the cI repressor protein and RFP under the Plux promoter. The cI repressor protein then binds to the operator of the sixth construct, inhibiting the production of GFP. |
Consequently, the output is red. | Consequently, the output is red. | ||
| + | </td></tr></table> | ||
<center> | <center> | ||
| - | [[Waterloo | Home ]] | + | [[Waterloo | Home ]] | [[Project | Project]] | [[Modelling | Mathematical Modelling]] | [[Construction_and_Testing | Construction and Testing]] | [[Future_Work | Future Work]] |
</center> | </center> | ||
Latest revision as of 03:58, 27 October 2007
Contents |
Background
Binary Addition
| Decimal (Base 10) |
Binary (Base 2) |
0 |
00 |
1 |
01 |
2 |
10 |
3 |
11 |
4 |
100 |
5 |
101 |
6 |
110 |
When working in binary, only two digits are used: 0 and 1. A single binary digit is called a bit. Counting proceeds as: To add two binary numbers, the process is much the same as adding two decimal (ordinary) numbers, except that instead of carrying when two digits add to ten, carrying must be performed when two digits add to two. In other words, 0 + 1 adds to 1, but 1 + 1 adds to 0 with a carry of 1, which gives 10 (just as in decimal 1 + 9 would add to 0 with a carry of 1, to give 10). A complete list of the possibilities is as follows:
Here is an example of long addition:
Half-Adder vs. Full-Adder
Any construct designed to add two numbers will either be a half-adder or a full-adder. A half-adder can only add together two single digits, whereas a full-adder is needed to add two numbers consisting of more than one digit.
For example, a half-adder could perform the addition 1 + 0 = 1, or 1 + 1 = 10, but it would take a full-adder to be able to perform 1100101 + 100101.
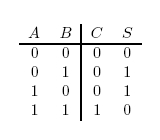
In terms of implementation, a half-adder accepts two inputs (the two digits to be summed) and returns two outputs (the "sum bit" and the "carry bit"). To add 1 + 1, the two inputs would each be 1, the sum bit would be 0, and the carry bit would be 1. A full list of the possibilities is shown in Figure 1.
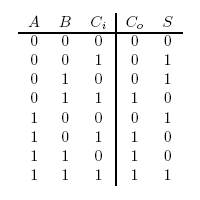
A full-adder is merely a half-adder that accepts an extra input; namely, the carry bit from another full-adder. Each full-adder is responsible for adding one pair of corresponding digits from the two numbers to be added, and it must add to that the carry bit from the previous full-adder. The full-adder will output the resulting sum bit and carry bit, and the process will continue until all the digits have been added. Such a chain of full-adders is called a ripple carry adder. See Figure 2 for a full list of possibilities.
Logic Gates and Implementing an Adder
A logic gate performs a logical operation on one or more logic inputs and produces a logic output. Usually the inputs and outputs are binary, meaning they each have a value of either 0 or 1. Also, it is often useful to think of of 0 as representing "false", and 1 as representing "true". A list of relevant logic gates is as follows:
- OR gate
- XOR gate
- AND gate
- NOT gate
For the following explanations, A and B represent statements that can be either true or false.
| Operator | Condition | Truth Table |
|---|---|---|
| a OR b | If a, b, or both are true | 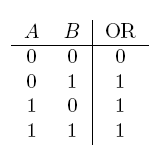 |
| a XOR b | If a and b are different | 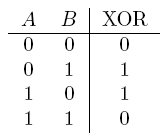 |
| AND | If both are true | 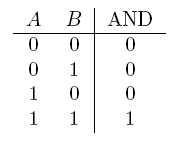 |
| NOT a | If a is false | 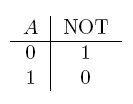 |
Using logic gates to make an adder
Given two binary inputs A and B, their sum can be computed by passing these inputs through various logic gates. The process is illustrated in Figures 4 and 5.
DNA as Logic Gates
Our project focuses on using DNA as logic gates. The output of a logical operation is the protein product of a certain gene; the inputs are external stimuli that cause allosteric changes in the conformation of proteins that can induce or inhibit transcription by acting on promoter elements. Whether or not the gene is turned 'on' or 'off' depends on the logic gate implemented.
For two inputs, the "presence" or "absence" of input A and the "presence" or "absence" of protein B (both representing 0 or 1 as inputs) would result in an output of either the "presence" or "absence" of protein X (where "presence" and "absence" should be read as high and low intensity/concentration, respectively).
For example, consider a regulated gene G that codes for protein X. By default, the gene is not expressed (to be precise, there is a low basal level of expression that we can disregard). If the inputs A and B are on and together can turn on expression of gene G, the expressed protein X represents the output of an AND gate. This is the type of approach used to construct our biological adder.
Project Details
Input and Output
|
As a half-adder, our device requires two binary inputs; the possible 1 and 0 values of these inputs are represented by the presence and absence of two stimuli. For the first input, the presence of red light represents a 0 and the absence represents a 1. For the second input, the absence of tetracycline represents a 0 and the presence represents a 1. We chose to use light as an input because it does not require altering the media, it can be turned on and off rapidly, and it has extremely high resolution and accuracy. The red light will be detected by Cph8, the previously used Cph1/EnvZ fusion protein. Tetracycline was used as a second input since it inactivates the repressor TetR, thereby derepressing expression at the PtetR locus. Depending on the result of the calculation, the bacteria will produce either red fluorescent protein (RFP), green fluorescent protein (GFP), or neither. A diagram of the biological half adder in culture is shown above, depicting the possible outcomes for each combination of inputs. |
Molecular Mechanism
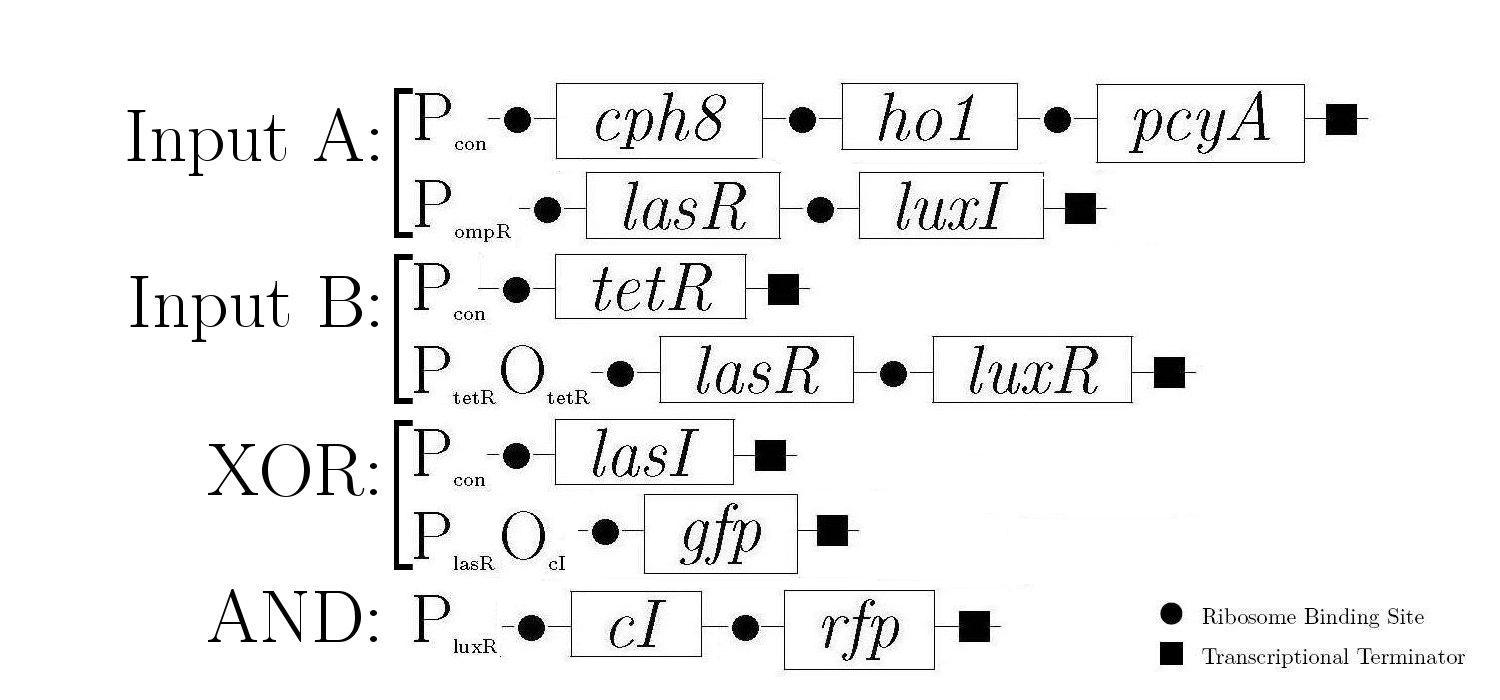
As components of a natural quorum sensing system, LuxR and LuxI proteins are ideal for producing the AND logic function required to create 1-bit half-adder. LuxR enhances transcription at Plux when activated by an inducer produced by LuxI. The expression of both LuxR and LuxI is therefore necessary to "turn on" the promoter Plux. LasR and LasI have analogous roles in another quorum sensing system, and contribute to the XOR logic function in our design. Below is a diagram showing all of the gene constructs that are involved in the biological half adder (these will ultimately be included on a single plasmid, but are here shown separately for ease of explanation).
The products in the first, third, and fifth constructs are always produced while the other constructs are controlled by various proteins that either induce or inhibit the production of the proteins that these genes encode.
The behaviour of the half-adder can be described by four possible cases which are simulated in the genetic system as follows:
Home | Project | Mathematical Modelling | Construction and Testing | Future Work