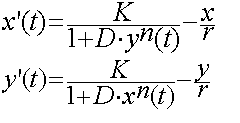Saint Petersburg\Theoretical study
From 2007.igem.org
m (Theoretical study moved to Saint Petersburg\Theoretical study) |
|||
| (3 intermediate revisions not shown) | |||
| Line 3: | Line 3: | ||
| - | == Trigger == | + | ==Simple Trigger == |
| + | |||
The main part of system is simple trigger, containing two repressors and to promotors. | The main part of system is simple trigger, containing two repressors and to promotors. | ||
Each repressor inhibit another repressor synthesis. | Each repressor inhibit another repressor synthesis. | ||
| - | + | [[Image:Saint_Petersburg_Trigger_sh.jpg|frame|left|Simple trigger]] | |
| - | [[Image:Saint_Petersburg_Trigger_eq.gif]] | + | Concentration of inhibitors x and y describes the next system equations. |
| + | |||
| + | [[Image:Saint_Petersburg_Trigger_eq.gif|Simple trigger equations]] | ||
Here the constants D, K, n and r are used to describe the promoter strength and inhibition efficiency. | Here the constants D, K, n and r are used to describe the promoter strength and inhibition efficiency. | ||
| + | |||
| + | This system can hold state with high concentration of one inhibitor, and low concentraion of another inhibitor. | ||
| + | But we need to have ''only one'' stable state, another state must be unstable, and exist only in high copper concentrations. | ||
| + | |||
| + | == One-stable switch == | ||
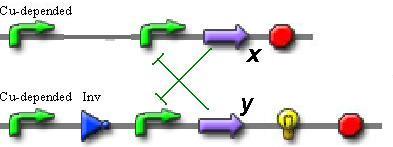
| + | To design a switch with one stable state we decided to use the constitutive promoter on the one hand of trigger, and copper-dependent promoter on the another hand. | ||
| + | So, this lead to such scheme: | ||
| + | [[Image:Saint-Petersburg_Trigger_Cu_sh.jpg|frame|left|Trigger with copper-depended promoter]] | ||
| + | |||
| + | Concentration of inhibitors x and y describes the next system: | ||
| + | [[Image:Saint-Petersburg_Trigger_Cu_eq.gif]] | ||
| + | |||
| + | Here the additive "1" in upper equation describes the constitutive promoter. | ||
| + | The additive R describes the additional level of expression, depending on the availability of copper. | ||
| + | |||
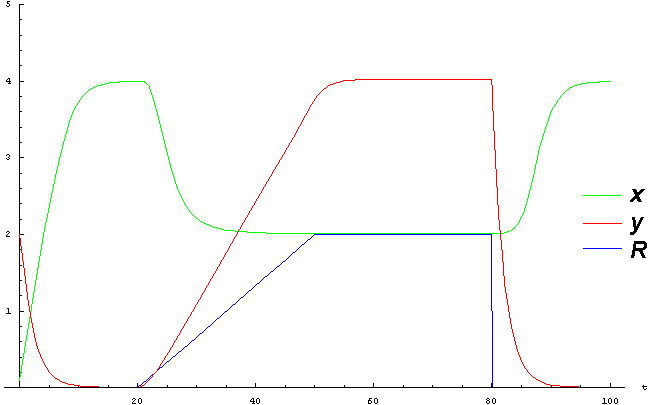
| + | Now, we can solve this equations and see, how additional expression level alternate the levels of x and y inhibitors. | ||
| + | |||
| + | [[Image:Saint-Petersburg_Trigger_Cu_graph.gif]] | ||
| + | |||
| + | Here we can see, that high concentration of inhibitor x, establishes wiry quickly, despite low initial level of x. | ||
| + | When we turn on the copper-induced promoter, we can alterate the level of inhibitors y and x, producing the signal. | ||
| + | |||
| + | Now, let's look, what happened, if we alternate the level of activation slowly. | ||
| + | |||
| + | [[Image:Saint-Petersburg_Trigger_Cu_graph_2.gif]] | ||
| + | |||
| + | Here we can see the alteration of y concentration, but it happened rather slow. | ||
| + | Increasing y concentration limited by increasing R from the copper-depended promoter. | ||
| + | |||
| + | Next time we will try to make the switching faster. | ||
| + | |||
| + | |||
| + | == Trigger with Cu-inverter == | ||
| + | |||
| + | In this work we tried to use trigger with inverted copper-depended promoter instead of constitutive. | ||
| + | So, this lead to such scheme: | ||
| + | |||
| + | [[Image:Saint-Petersburg_Trigger_invCu_sh.jpg|frame|left|Trigger with two copper-depended promoters]] | ||
| + | |||
| + | Concentration of inhibitors x and y describes the next system: | ||
| + | [[Image:Saint-Petersburg_Trigger_invCu_eq.gif]] | ||
| + | |||
| + | Here we can see the additive "Rmax - R" instead of 1 (in previous equation system). | ||
| + | |||
| + | Then, we can solve this system under the different R levels | ||
| + | [[Image:Saint-Petersburg_Trigger_invCu_graph.gif]] | ||
| + | |||
| + | In this scheme the alteration of repressor y level are faster. For my mind, this is enough to construct the fast switch. | ||
Latest revision as of 14:09, 26 October 2007
The Tri-stable Toggle Switch project was performed by Brown iGEM2006 team, but we need to adapt this to our needs.
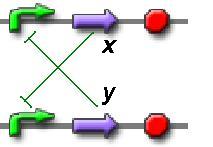
Simple Trigger
The main part of system is simple trigger, containing two repressors and to promotors. Each repressor inhibit another repressor synthesis.
Concentration of inhibitors x and y describes the next system equations.
Here the constants D, K, n and r are used to describe the promoter strength and inhibition efficiency.
This system can hold state with high concentration of one inhibitor, and low concentraion of another inhibitor. But we need to have only one stable state, another state must be unstable, and exist only in high copper concentrations.
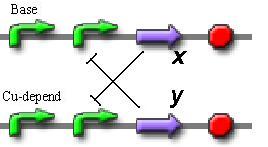
One-stable switch
To design a switch with one stable state we decided to use the constitutive promoter on the one hand of trigger, and copper-dependent promoter on the another hand. So, this lead to such scheme:
Concentration of inhibitors x and y describes the next system:
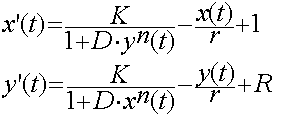
Here the additive "1" in upper equation describes the constitutive promoter. The additive R describes the additional level of expression, depending on the availability of copper.
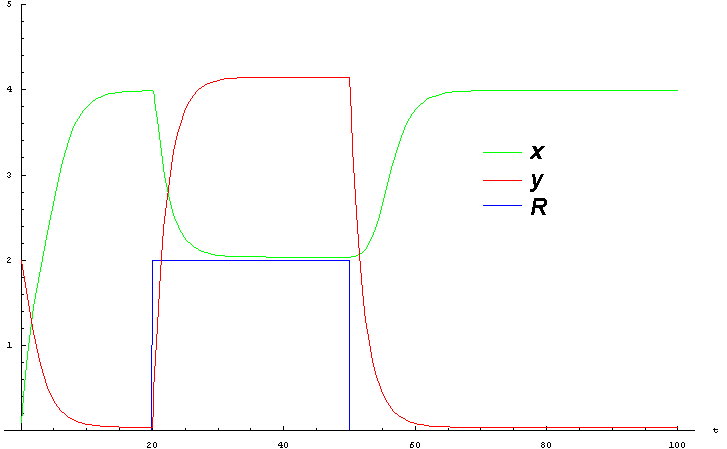
Now, we can solve this equations and see, how additional expression level alternate the levels of x and y inhibitors.
Here we can see, that high concentration of inhibitor x, establishes wiry quickly, despite low initial level of x. When we turn on the copper-induced promoter, we can alterate the level of inhibitors y and x, producing the signal.
Now, let's look, what happened, if we alternate the level of activation slowly.
Here we can see the alteration of y concentration, but it happened rather slow. Increasing y concentration limited by increasing R from the copper-depended promoter.
Next time we will try to make the switching faster.
Trigger with Cu-inverter
In this work we tried to use trigger with inverted copper-depended promoter instead of constitutive. So, this lead to such scheme:
Concentration of inhibitors x and y describes the next system:
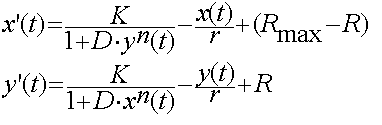
Here we can see the additive "Rmax - R" instead of 1 (in previous equation system).
Then, we can solve this system under the different R levels
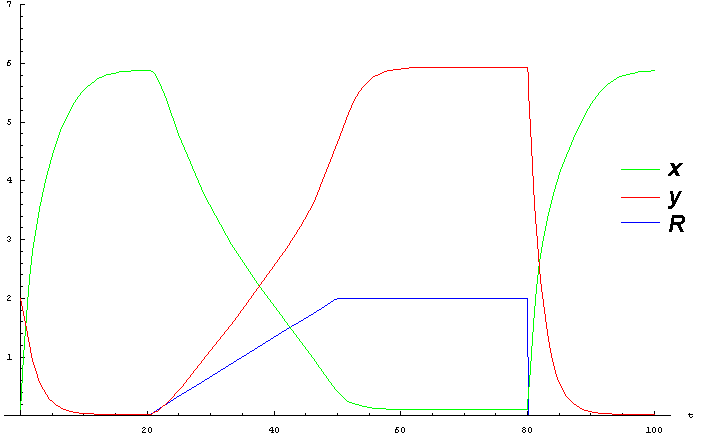
In this scheme the alteration of repressor y level are faster. For my mind, this is enough to construct the fast switch.