Edinburgh/DivisionPopper/Modelling
From 2007.igem.org
Luca.Gerosa (Talk | contribs) (→ODEs (deterministic and continuous)) |
Luca.Gerosa (Talk | contribs) (→ODEs (deterministic and continuous)) |
||
| Line 54: | Line 54: | ||
====ODEs (deterministic and continuous)==== | ====ODEs (deterministic and continuous)==== | ||
| - | We define a set of ordinary differential equations that represents the behaviour of a individual cell during time. For first, we define a set of equations for each one of the three phases (''Forward'', ''Flipping'', ''Backward'') and then we construct a unified set of equations by using two support functions. | + | We define a set of ordinary differential equations that represents the behaviour of a individual cell during time. For first, we define a set of equations for each one of the three phases (''Forward'', ''Flipping'', ''Backward'') and then we construct a unified set of equations by using two support functions. The concentrations in which we are interested are obviously GFP and RFP concentrations. |
| - | The biological mechanisms (or processes) we need to | + | The biological mechanisms (or processes) we need to represent are: gene expression of proteins and degradation of proteins. |
| - | We assume gene expression of a protein to be in | + | We assume gene expression of a protein to be in on or off state and, when in the on state, to be expressed at a constant rate. |
| - | We assume degradation of a protein to be | + | We assume degradation of a protein to be rate dependent on the amount of protein present. |
| - | Thus the | + | Thus the variables are: |
* GFP expression rate (mol/sec) called ''GFPexp'' | * GFP expression rate (mol/sec) called ''GFPexp'' | ||
| Line 64: | Line 64: | ||
* GFP degradation rate (1/sec) called ''GFPdeg'' | * GFP degradation rate (1/sec) called ''GFPdeg'' | ||
* RFP degradation rate (1/sec) called ''RFPdeg'' | * RFP degradation rate (1/sec) called ''RFPdeg'' | ||
| + | |||
| + | For the '''Forward Phase''' the equations are: | ||
====CTMC (stochastic and discrete)==== | ====CTMC (stochastic and discrete)==== | ||
Revision as of 13:35, 14 September 2007
MENU : Introduction | Applications | Design | Modelling | Status | References
This pages contains the mathematical and computational models we constructed in order to analyze the behaviour of the Division PoPper system. You can find the model of two systems (the proof of concept construct or the whole construct), different views on the system (the single cell behaviour or the behaviour of the population), different approaches to modeling (ODEs, CTMC, hybrid). Look at the table of contests belove for the section you are interested in.
Contents |
The proof of concept system
As explained in the design section, the first part of our project consists in the realization of a proof of concept system. This is a smaller and less complex construct that we use to test our main assumption: the DNA region in between the two Dif sites is "flipped" (reversed) at each cell division. The model should help us in answering the following questions:
- Is the system working well with standard E.Coli division time?
- Is the system working well with normal GFP,RPF Expression and degradation rate?
- How can we tune these parameters in order to have meaningful tests from the construct in the lab?
Since the mechanisms and the values that characterize the system are sometimes not known or time consuming/difficult to discovery in the lab, we use the models as "in silico" test. Thus our models should be dependent (functions of) on the following quantities:
- Cell division frequency (units: minutes): is the time elapsed from one division to the next one.
- Flipping duration (units: minutes): is the time elapsed from starting the flipping to the complete execution.
- GFP/RFP Expression rate (units: protein per second): the rate at which fluorescent proteins are expressed.
- GFP/RFP Degradation rate (units: protein per second): the rate at which fluorescent proteins degrade.
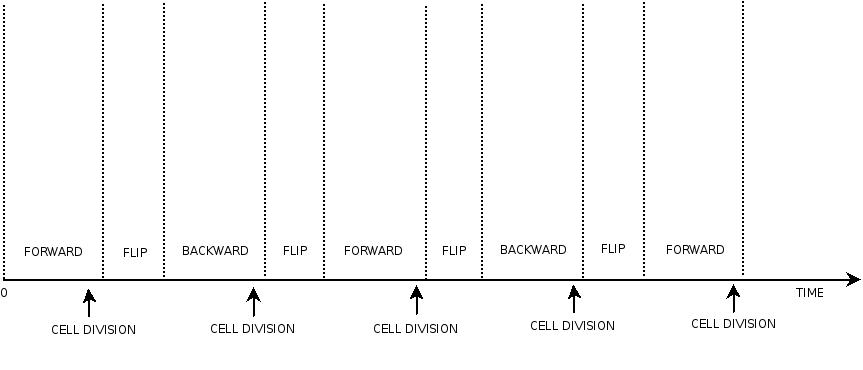
In order to construct the proper model, we need to identify which are the dynamics of the system. Since the real biological mechanisms are too complex, several approximations and abstractions are introduced at this step. In this sense, we can simplify the dynamics of the system by observing that three are the states in which our construct can be during the time evolution: Forward, Flipping and Backward phase. This three phases happen in a order controlled by cell division. In detail:
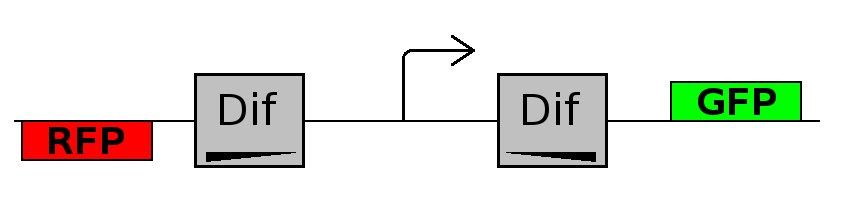
- Forward phase: The system starts in this phase. It is the phase in which the promoter is oriented in the 5' to 3' direction, thus controlling the expression of GFP coding region. In this phase in the cell there is expression of GFP and no expression of RFP.
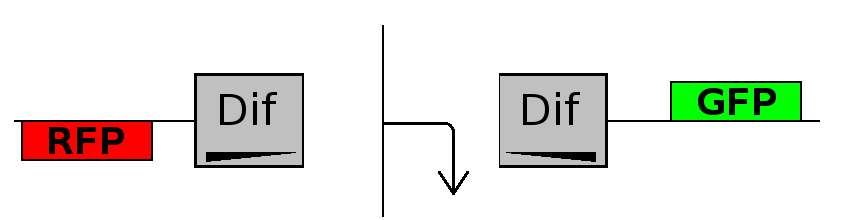
- Flipping phase: The system is in this phase when the recombinase activity has been initialized and not yet concluded. In this phase in the cell we assume there is no expression of GFP and no expression of RFP because the two coding regions are not any longer controlled by the promoter regulatory effect.
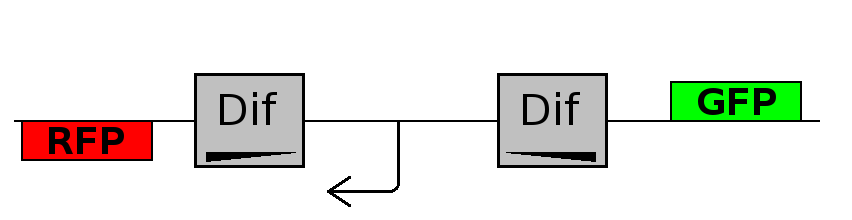
- Backward phase: It is the phase in which the promoter is oriented in the 3' to 5' direction, thus controlling the expression of the RFP coding region. In this phase in the cell there is expression of RFP and no expression of GFP.
This three are the states (phases) in which the proof of concept system can be during its time course evolution. The system passes through these phases according to cell division timing and following the pattern: forward phase, flipping phase, backward phase, flipping phase and so on. A picture clarifies better the time course behaviour:
The arrows mark the points in time in which a cell division starts.
Modelling a single cell
As first step, we are interested in investigating the behaviour of the system at the level of a single cell. In particular, we are interested in following the course time behaviour of one single cell line. This means that in our model we start observing a individual cell behaviour and at each cell division we follow one of the two daughter cells and so on.
For that we construct two different approaches: using Ordinary Differential Equation and Stochastic Process Algebras. The first is deterministic (the behaviour of the system is defined only by the value of the variables) and treats population of molecules as a continuos value. It gives us a general understanding of what is the "avarage" behaviour of the time evolution of a cell. The second is stochastic (the behaviour of the systems is defined by the value of normal and random variables) and treats the population of molecules as a discrete value. It gives us (theoretically) a better understanding of which can be the different trajectory in behaviour of individual cells and helps us in simulating then the behaviour of a population.
ODEs (deterministic and continuous)
We define a set of ordinary differential equations that represents the behaviour of a individual cell during time. For first, we define a set of equations for each one of the three phases (Forward, Flipping, Backward) and then we construct a unified set of equations by using two support functions. The concentrations in which we are interested are obviously GFP and RFP concentrations. The biological mechanisms (or processes) we need to represent are: gene expression of proteins and degradation of proteins. We assume gene expression of a protein to be in on or off state and, when in the on state, to be expressed at a constant rate. We assume degradation of a protein to be rate dependent on the amount of protein present. Thus the variables are:
- GFP expression rate (mol/sec) called GFPexp
- RFP expression rate (mol/sec) called RFPexp
- GFP degradation rate (1/sec) called GFPdeg
- RFP degradation rate (1/sec) called RFPdeg
For the Forward Phase the equations are: