Tokyo/Model
From 2007.igem.org
(Difference between revisions)
| Line 7: | Line 7: | ||
[[Image:model1.jpg]] | [[Image:model1.jpg]] | ||
| - | |||
The system is stable containing nodes A and B at certain ratio. | The system is stable containing nodes A and B at certain ratio. | ||
| Line 14: | Line 13: | ||
[[Image:model2.jpg]] | [[Image:model2.jpg]] | ||
| - | |||
Removed of node A, the system contains only node B and becomes unstable. Node B detects the removal of node A from the system and knows that there is only node B left. | Removed of node A, the system contains only node B and becomes unstable. Node B detects the removal of node A from the system and knows that there is only node B left. | ||
| Line 21: | Line 19: | ||
[[Image:model3.jpg]] | [[Image:model3.jpg]] | ||
| - | |||
| - | |||
In an unstable state, some node B become A while the others remain B. The system then becomes stable again. | In an unstable state, some node B become A while the others remain B. The system then becomes stable again. | ||
Revision as of 14:04, 16 October 2007
Model
To establish a system following Pareto’s principle, the system must satisfy the following three cases. In our model, all nodes have the same genetic circuits and take two states, A (worker) and B (idler), depending on the surrounding circumstances.
Condition 1. Bistable state
The system is stable containing nodes A and B at certain ratio.
Condition 2. Unstable state with node A removed
Removed of node A, the system contains only node B and becomes unstable. Node B detects the removal of node A from the system and knows that there is only node B left.
Condition 3. From unstable to stable state
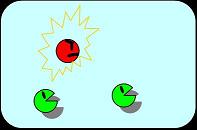In an unstable state, some node B become A while the others remain B. The system then becomes stable again.
