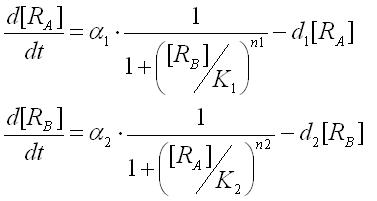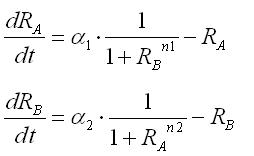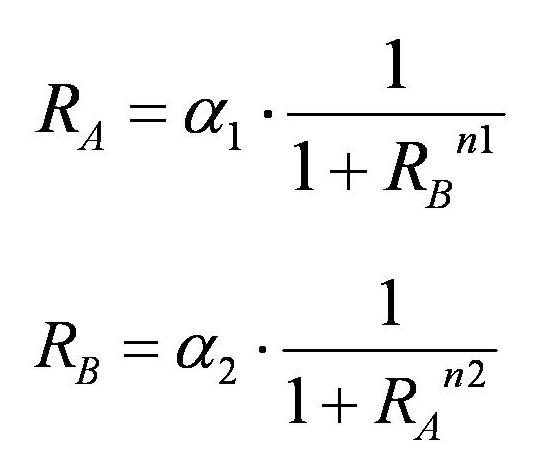Tokyo/Formulation/1.toggle model
From 2007.igem.org
| Line 4: | Line 4: | ||
<br>[[Image:expression1-1.jpg|200px|]] [[Image:parameter1-1.jpg|200px|]] | <br>[[Image:expression1-1.jpg|200px|]] [[Image:parameter1-1.jpg|200px|]] | ||
| - | <br>And,we normalize these expressions. | + | <br>And,we normalize these expressions to analyze easily.So,ODEs become dementionless. |
| + | なるってbecomeであってる?? | ||
<br>[[Image:expression1-2.jpg|200px|]] | <br>[[Image:expression1-2.jpg|200px|]] | ||
Revision as of 17:38, 21 October 2007
1.toggle model
First,we obtain the ordinary differential equations(ODEs) of the toggle switch.
And,we normalize these expressions to analyze easily.So,ODEs become dementionless.
なるってbecomeであってる??
if the system goes to the steady state,time variation equal to zero.So we solve righe-hand side=0.
These graph are below.The lines of graph are nullcline,and the intersection of nullclines is the equillibrium point.
About parameters,we use three sets of parameters.
1)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.
2)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.
3)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.
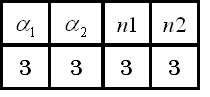

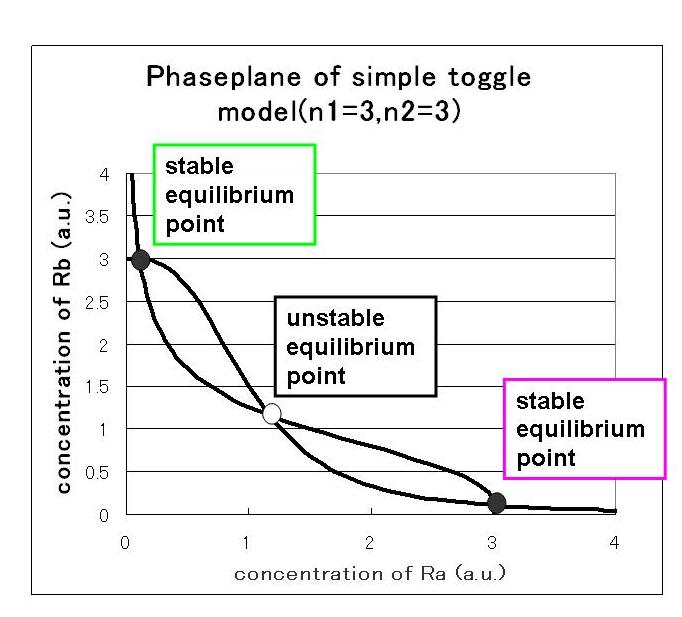
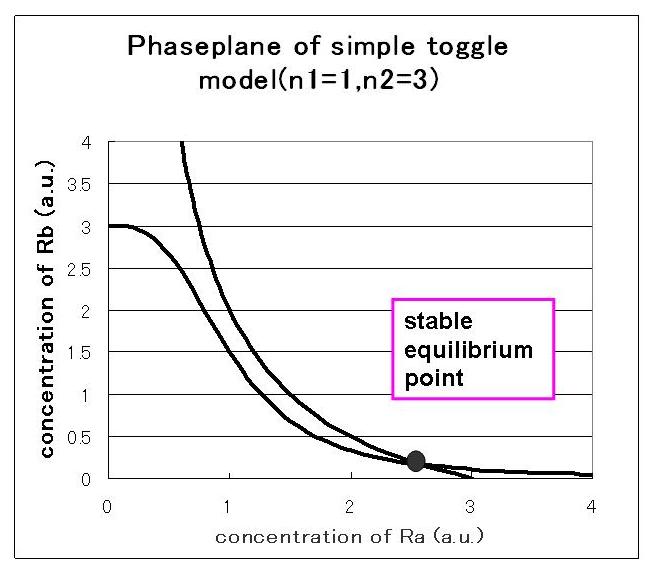
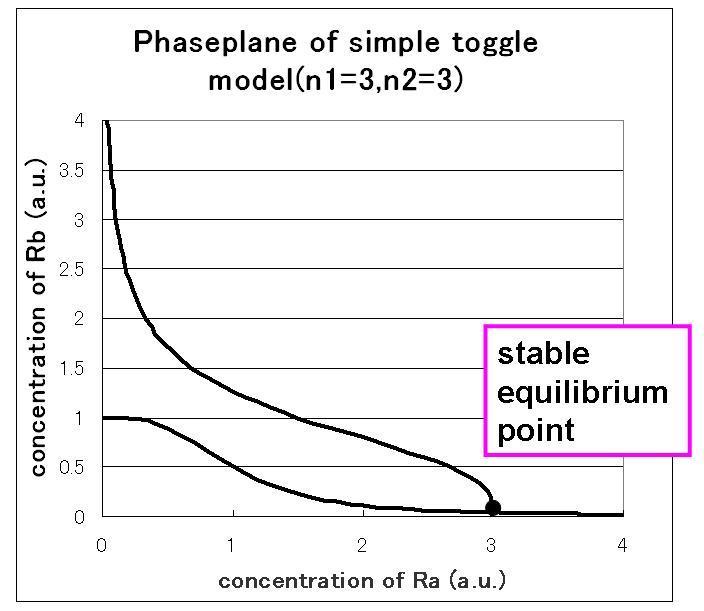
we correlate phaseplane analysis and simulation results.
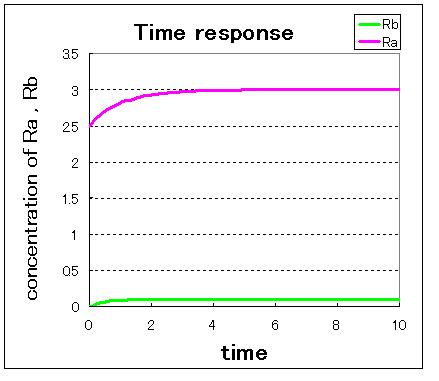
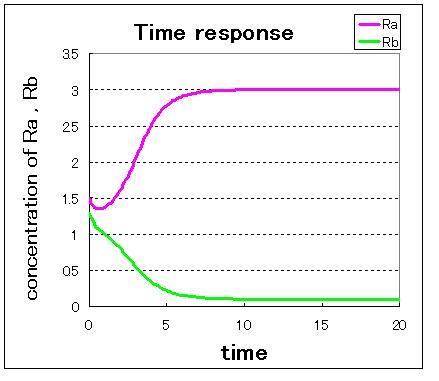
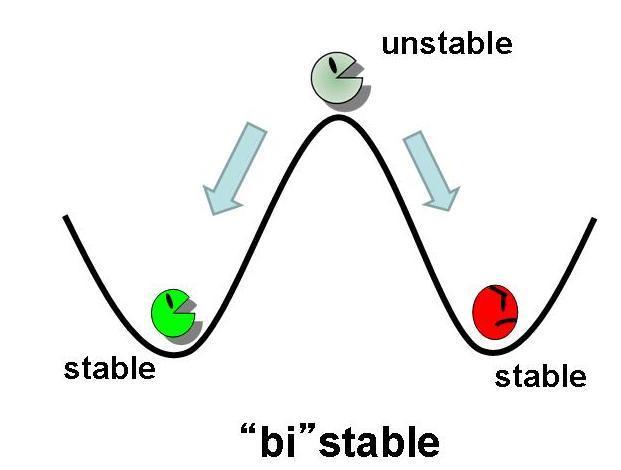
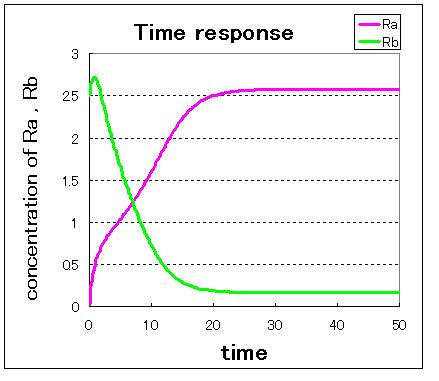
First,we simulate about the phaseplane of two stable equilibrium points(the upper left figure) and use three kinds of initial values.
1. (Ra:low , Rb:high) 2. (Ra:high , Rb:low) 3. (Ra:middle , Rb:middle)
安定点B付近から始めるとB状態で安定し,安定点A付近から始めるとA状態で安定しているのが分かる.
不安定点付近から始めるとどちらかで安定化する.
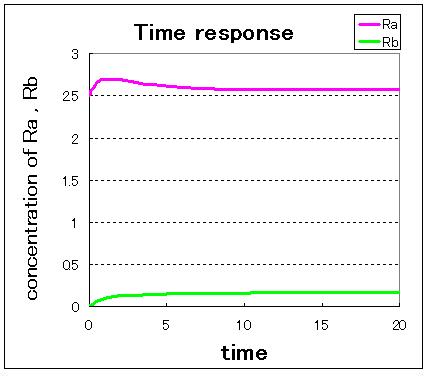
Next,
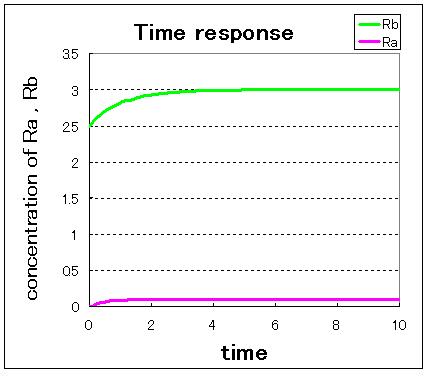
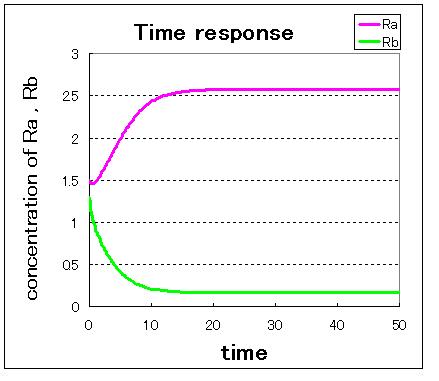
次に,安定点が一つしかない場合のシミュレーション結果は下のようになる.
安定点が一つしかない場合は,安定点B付近から始めてもA状態で安定化してしまうのが分かる.
As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.