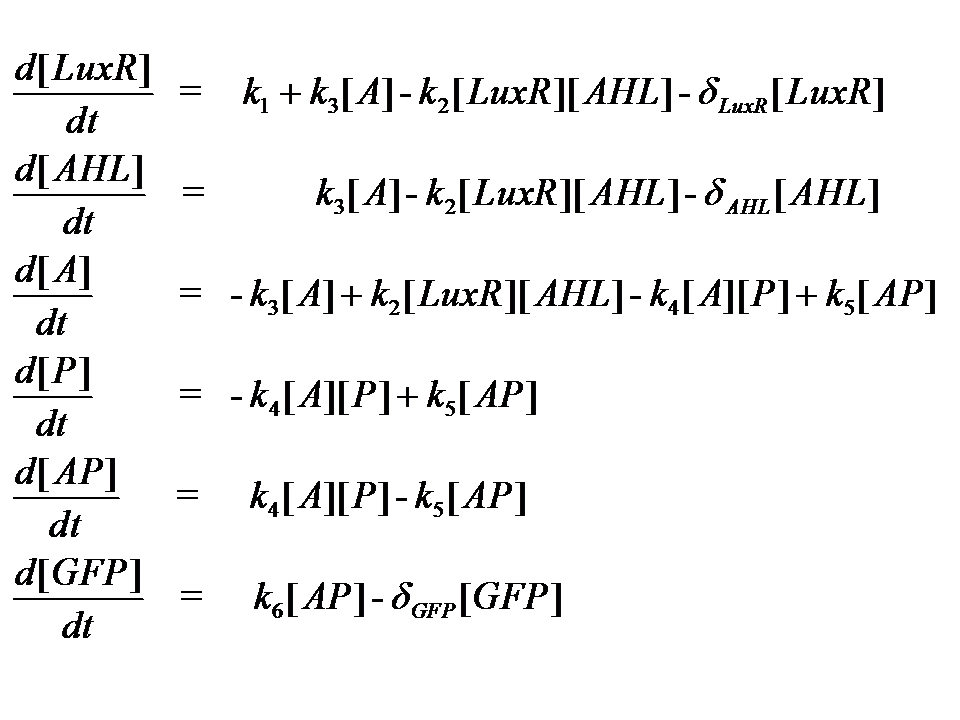Imperial/Dry Lab/Modelling
From 2007.igem.org
(→Model 1) |
(→Motif) |
||
| Line 54: | Line 54: | ||
==References== | ==References== | ||
| - | == | + | ==Log== |
*Images - black borders, pastel backgrounds (pale) - see QS image | *Images - black borders, pastel backgrounds (pale) - see QS image | ||
*Equations - bordered | *Equations - bordered | ||
| + | *Improve appearance of eqns | ||
Revision as of 01:33, 22 October 2007
Contents |
Model Development for Infector Detector
Formulation of the problem
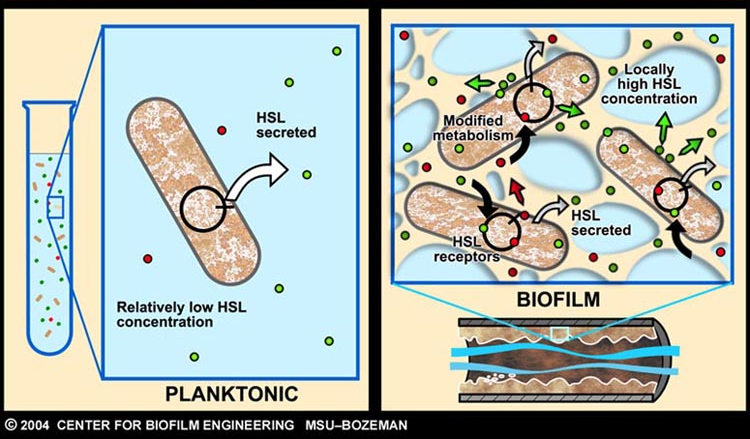
As described earlier, catheter-associated urinary tract infection (CAUTI) in the clinical setting is a prevalent problem with extensive economic impact. The underlying cause of many such infections can be attributed to the formation of biofilm, by aggregating-bacteria on the surface of urinary catheters.
Infector Detector (ID) is a simple biological detector, which serves to expose bacterial biofilm. It functions by exploiting the inherent AHL (Acetyl Homoserine Lactone) production employed by certain types of quorum-sensing bacteria, in the formation of such structures.
Our project attempts to improve where previous methods of biofilm detection have proven ineffective: first and foremost, by focussing on the sensitivity of the system, to markers of biofilm: in this case, low levels of AHL production (which represents the bacterial "chatter" of such aggregating bacteria).
In doing so, a complete investigation of the level of sensitivity to AHL concentration needs to be performed - in other words, what is the minimal AHL concentration for appreciable expression of a chosen reporter protein. Furthermore, establish a functional range for possible AHL detection. How does increased AHL concentration impact on the maximal output of reporter protein?
Finally, how can the system performance be tailored, by exploiting possible state variables (e.g. varying initial LuxR concentration and/or concentration of pLux promoters).
The system performance here revolves most importantly around AHL sensitivity; however, the effect on the maximal output of fluorescent reporter protein and response time is, likewise, of great importance.
Selection of Model Design and Structure
Since the novelty of our solution revolves around the use of cell-free systems as a "bacterial-free" solution in the clinical setting, a simple system is selected. Our approach involves a modified version of the bioluminescence machinery employed by the bacterium Vibrio Fischeri.
In fact, the characterization of this machinery, forms the setting for the first detailed description of the above-mentioned quorum-sensing phenomenon (Engebrecht and Silverman, 1984 and Engebrecht et al., 1983). A system which employs two regulatory proteins LuxR and LuxI, which, together with the autoinducer protein, AHL, control the expression of the in-house reporter (luciferase).
Our system maintains the general flavour of this configuration; involving a marginally-varied sensor and reporter element. In fact, an already present system is utilized, for its simplicity and good definition - [http://partsregistry.org/Part:BBa_T9002| T9002]. This forms our construct 1.
One of the questions posed in the formulation of the model, involved exploring means of "tweaking" the system to achieve improved performance (sensitivity/maximal output/response time). A possible solution could involve introducing purified LuxR into the system, and in this way impose steady-state far sooner than construct 1. Theoretically, this should shorten response time. It is for this reason, that a second construct will be investigated. Construct 2 thus differs only wrt the elimination of the constitutive promoter pTET. (here, LuxR is introduced directly).
~~Insert diagram illustrating both constructs
~~Insert diagram illustrating both interaction of molecules
~~Insert diagram illustrating sensor and reporter elements
Establishing a model
Duis autem vel eum iriure dolor in hendrerit in vulputate velit esse molestie consequat, vel illum dolore eu feugiat nulla facilisis at vero eros et accumsan et iusto odio dignissim qui blandit praesent luptatum zzril delenit augue duis dolore te feugait nulla facilisi
Approach
At reasonably high molecular concentrations of the state variables, a continuous model can be adopted, which is represented by a system of ordinary differential equations.
It is for this reason that our approach to modelling the system follows a deterministic, continuous approximation. In developing this model, we were interested in the behaviour at steady-state, that is when the system has equilibrated and the concentrations of the state variables remain constant.
We can condition the system in various manners, but for the purposes of our project, we will seek a formulation which is valid for both constructs considered, i.e. the governing equations are a represenation of both constructs.
The only difference is with regards to the parameter k1, the maximum transcription rate of the constitutive promoter (pTET) in Construct 1.
Thus k1 = 0 for construct 2 (which lacks pTET).
Our initial approach assumed that energy would be in unlimited supply, and that our system would eventually reach steady-state (Model 1).
Model 1
References
Log
- Images - black borders, pastel backgrounds (pale) - see QS image
- Equations - bordered
- Improve appearance of eqns