From 2007.igem.org

Revision as of 12:10, 22 October 2007 (view source) Vieira (Talk | contribs) (→'''Case 1''') ← Older edit		Revision as of 12:11, 22 October 2007 (view source) Vieira (Talk | contribs) (→'''''We produce this set of rules''''') Newer edit →
Line 23:		Line 23:
	='''Case 1'''=		='''Case 1'''=
-	='''''We produce this set of rules'''''=	+	=='''''We produce this set of rules'''''==
	<br>		<br>

---

Revision as of 12:11, 22 October 2007

Contents 1 Spacial simulation 2 We make some hypothesis: 3 We have 3 entities in our model 4 Case 1 4.1 We produce this set of rules 4.2 Initial state 4.3 Parameters 4.4 Output

Spacial simulation

We try with this work to characterize the diffusion of the DAP and the effect on the cells. We have a growing culture with germinal cells and somatic cells.
We want to see if we can have different kinds of evolution for our cells

We make some hypothesis:

We work with a evolving population ( death for BactS and division BactG).

• Case 1 : The differentiation is DAP dependent, it's append when the cell as enough DAP to evolve but not enough to divide.
  
• Case 2 : The differentiation has a constant rate, it will be the same rate for each division cycle

The DAP is made in bacteria S, the production rate is the difference between the total production and self consummation
We consider a global variable DAP (no internal/external DAP)
The DAP is comsumme in bacteria G


All the cells grow

We have 3 entities in our model

Bact it has a concentration internal of DAP and a radius. It's a cell in our automaton
BactS is a Bact which produce DAP and can grow
BactG is a Bact which consume DAP and can divide or differentiate

Case 1

We produce this set of rules

Mecanic forces

• We create a spring betwen the center of each Bac, then we compute the forces related to this spring and we update the position of the cells (adding noise to it)
  

For bactS

• DAPe = DAPe + DAPe_diffused_in_neighborhood + DAPi_diffused_from_the_BactS
  
• DAPi= DAPi +DAPi_produced - DAPi_diffused_from_the_BactS
  

For BactG

• DAPe=DAPe + DAPe_diffused_in_neighborhood - DAPi_diffused_from_the_BactG
  
• DAPi= DAPi -DAPi_consummate + DAPi_diffused_from_the_BactG
  
• BactG = if minimal DAPi for differentiation < DAPi < maximal DAPi for differentiation BactS else stay BactG

Initial state

We use a 30x30 cells automaton. All cells are BactG excepted 4 BactS which are placed randomly on the automaton

Parameters

We have 8 parameters and we can had noise for each of them.
In BactS:

• Dap export
  
• Dap import
  
• Dap production
  

In BactG:

• Dap export
  
• Dap import
  
• Dap consummation
  
• Minimal Dap needed for differentiation
  
• Maximal Dap needed for differentiation
  

Output

The output is two animated pictures one showinf the differntiation the other the diffusion of DAPe

• The first picture show the diffusion of DAP

We can see a front wave in light blue after that there is a dark blue area in which the systeme is stable the concentration doesn't evolve.

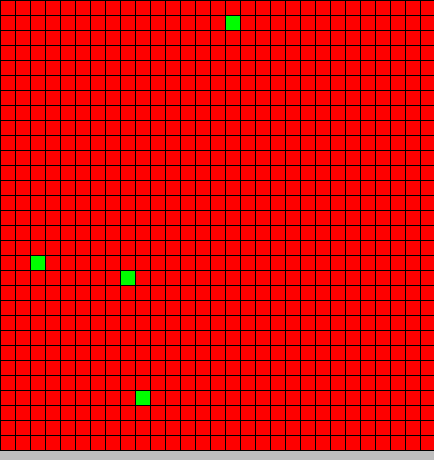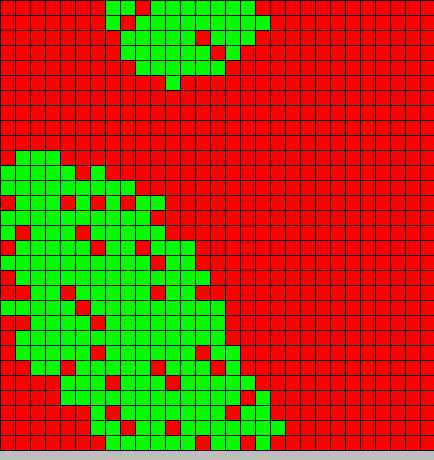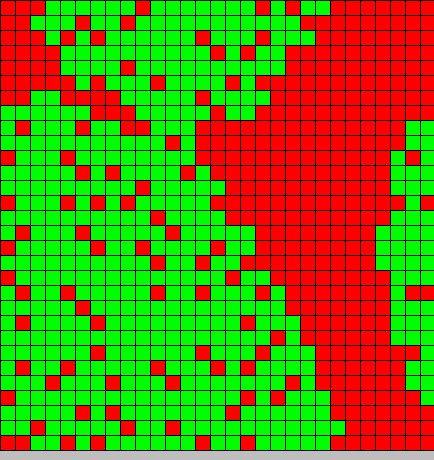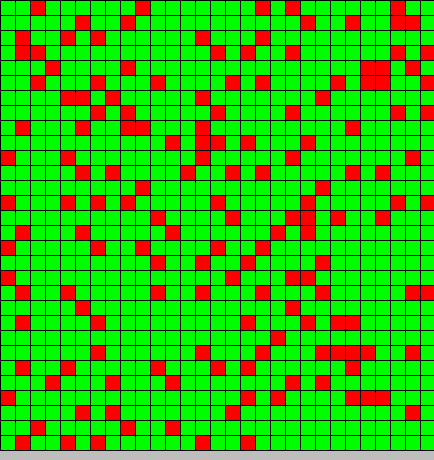
• The second picture show the differention

Red BactG

Green BactS

The differentiation follow the wave front

After playing with the parameters, we can deduct 2 important things:

• The inhibition most be strong and effective (we play with the minimal and maximal value of DAP for differentiation)

if it isn't the case the system collapse all the bactG stay BactG if the inhibition is too strong or switch to BactS if the inhibition is not enough strong.

• The production and diffusion of DAP will be a critical factor

The DAP has to be produce then he will be exported, it will diffuse in the medium and will be imported

There is no proof of a special systme to import or export DAP, so for each step there is a large amount of DAP lost.