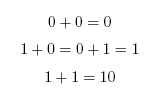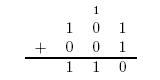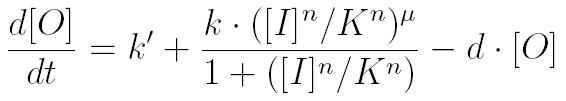Project

From 2007.igem.org

Revision as of 08:51, 26 October 2007

Background

Binary Addition

When working in binary, only two digits are used: 0 and 1. A single binary digit is called a bit. Counting proceeds as: To add two binary numbers, the process is much the same as adding two decimal (ordinary) numbers, except that instead of carrying when two digits add to ten, carrying must be performed when two digits add to two. In other words, 0 + 1 adds to 1, but 1 + 1 adds to 0 with a carry of 1, which gives 10 (just as in decimal 1 + 9 would add to 0 with a carry of 1, to give 10). A complete list of the possibilities is as follows:

Here is an example of long addition:

Half-Adder vs. Full-Adder

Figure 1: Half-Adder Truth Table

Figure 2: Full Adder Truth Table

Any construct designed to add two numbers will either be a half-adder or a full-adder. A half-adder can only add together two single digits, whereas a full-adder is needed to add two numbers consisting of more than one digit.

For example, a half-adder could perform the addition 1 + 0 = 1, or 1 + 1 = 10, but it would take a full-adder to be able to perform 1100101 + 100101.

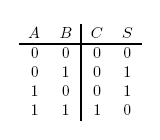
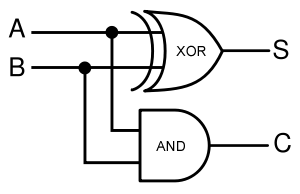
In terms of implementation, a half-adder accepts two inputs (the two digits to be summed) and returns two outputs (the "sum bit" and the "carry bit"). To add 1 + 1, the two inputs would each be 1, the sum bit would be 0, and the carry bit would be 1. A full list of the possibilities is shown in Figure 1.

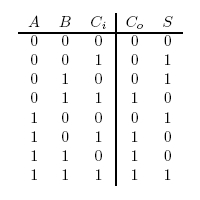
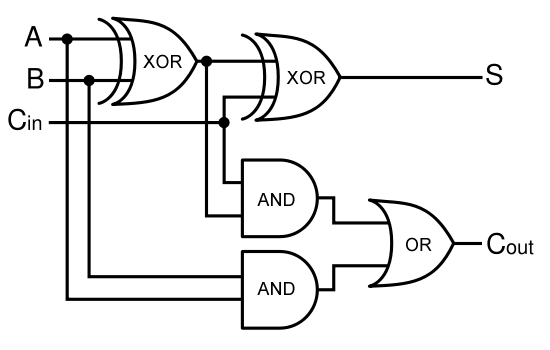
A full-adder is merely a half-adder that accepts an extra input; namely, the carry bit from another full-adder. Each full-adder is responsible for adding one pair of corresponding digits from the two numbers to be added, and it must add to that the carry bit from the previous full-adder. The full-adder will output the resulting sum bit and carry bit, and the process will continue until all the digits have been added. Such a chain of full-adders is called a ripple carry adder. See Figure 2 for a full list of possibilities.

Logic Gates and Implementing an Adder

A logic gate performs a logical operation on one or more logic inputs and produces a logic output. Usually the inputs and outputs are binary, meaning they each have a value of either 0 or 1. Also, it is often useful to think of of 0 as representing "false", and 1 as representing "true". A list of relevant logic gates is as follows:

• OR gate
• XOR gate
• AND gate
• NOT gate

For the following explanations, A and B represent statements that can be either true or false.

OR Gate

Consider the statement "A OR B". If either A or B is true, the statement is said to be true. The only time this statement will be false is when both A and B are false. This is the meaning of the OR operation.

An OR gate accepts two binary inputs, where a 1 represents "true" and a 0 represents "false". The output of the OR gate is also binary, and similarly represents either "true" or "false".

To illustrate,

0 OR 0 = 0

1 OR 0 = 0 OR 1 = 1

1 OR 1 = 1

XOR Gate

XOR is an abbreviation for "exclusive OR". The XOR gate is similar to the OR gate, the only difference being that it will return false if both inputs are true.

For example,

1 XOR 0 = 1

1 XOR 1 = 0

AND gate

The AND gate will return 1 (true) only if both the inputs are 1 (true). Otherwise, it will return a 0.

To illustrate,

0 AND 0 = 0

1 AND 0 = 0 AND 1 = 0

1 AND 1 = 1

NOT gate

The NOT gate accepts one input, and simply switches its value.

NOT 1 = 0

NOT 0 = 1

Using logic gates to make an adder

Given two binary inputs A and B, their sum can be computed by passing these inputs through various logic gates. The process is illustrated in Figures 4 and 5.

Figure 4: Half-adder circuit diagram

Figure 5: Full-adder circuit diagram

DNA as Logic Gates

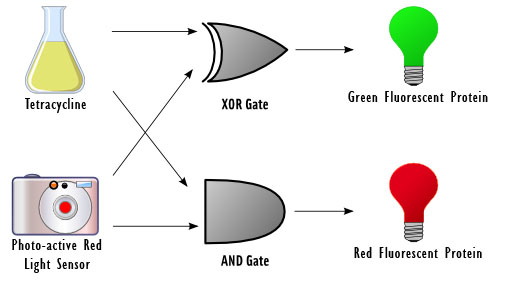
The focus of our project revolves around using DNA as logic gates. In essence, the output of a logical operation is the chemical produced by a certain gene, and the inputs are external stimuli that modify the conformation of proteins, which act on the promoters of the genes to induce or inhibit transcription depending on the specific logic gate implemented.

For example, consider a positively regulated gene G that codes for protein X. By default, the gene is not expressed. If the inputs A and B are on and inducing protein activity that turns on G, the expressed protein represents the output of an AND gate. The inputs would be the "presence" or "absence" of A and the "presence" or "absence" of B (both representing 0 and/or 1 as inputs), and the output would be the "presence" or "absence" of X (where "presence" and "absence" should be read as high and low intensity/concentration, respectively).

This is the type of approach used to construct our biological adder. Further details are given under the Project Details section.

Project Details

Inputs

As a half-adder, our cells require two binary inputs. We chose to use the presence or absence of red light as one input, and the presence or absence of the chemical tetracycline as another. For the first input, the presence of red light represents a 0 and the absence represents a 1. For the second input, the absence of tetracycline represents a 0 and the presence represents a 1.

We chose to use light as an input for the reasons that it does not require altering the media, it can be turned on and off rapidly, and it has extremely high resolution and accuracy. The red light will be detected by the previously used Cph1/EnvZ fusion protein ([http://partsregistry.org/Part:BBa_I15010 BBa_I15010]).

Tetracycline was used as a second input since it binds to the tetR repressor ultimately allowing for the production of the Green Fluorescent Protein (GFP) or Red Fluorescent Protein (RFP). It also will not interfere with the constitutive promoter and can be easily controlled.

Output

Depending on the result of the calculation, the bacteria will produce either red fluorescent protein (RFP), green fluorescent protein (GFP), or neither. The possible outcomes are as follows:

No Tetracycline & No red light ==> 0+0 ==> nothing

No Tetracycline & Red light ==> 0+1 ==> GFP

Tetracycline & No red light 1+0 ==> GFP

Tetracycline & red light ==> 1+1 ==> RFP

A diagram of the biological half adder in culture is shown below. It shows all outputs given all possible inputs.

Input and Outputs of the Biological Half Adder

Schematic Diagram

Schematic Design of Biological Half-Adder

Gene Diagram

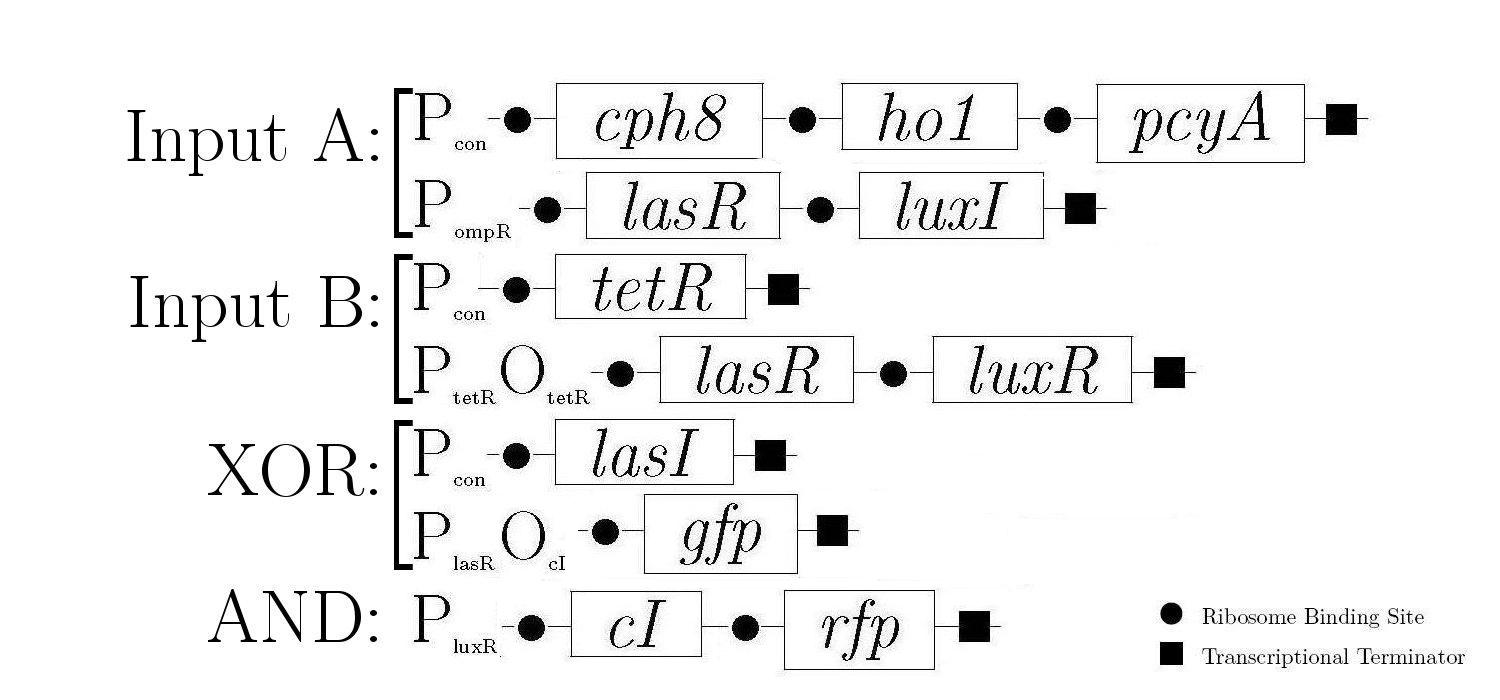
Gene Diagram for the Half Adder Construction

Construction

Construction Chart

Testing/Results

Testing Constructs

Making use of flurorescent proteins(GFP and RFP) as reporter genes - use of indicuble promoters to...

Comparing basal and induced expression levels for the quorum sensing promoters

CONSTRUCT	AIMS
	The quorum-sensing promoters: How active is 'unactivated' Plas and Plux? preliminary test for the basal levels of activity of the positively-controlled quorum sensing promoters
	The quorum-sensing constructs: How off is 'off' and how on is 'on'?</br> test for levels of expression in the unenhanced versus enhanced state xR must be expressed in same strain as Px; xI can be expressed in a different strain since its AHL is diffusable both strains grown in a single culture tube

Testing functionality of the various promoters

CONSTRUCT	AIMS
	The Omp promoter postively-controlled promoter activated by endogenous OmpR protein (sensitive to salt concentrations via EnvZ protein) test for activity using high salt levels in EnvZ+ strain test for activity using the photo-active red system in EnvZ- strain
	The Tet promoter and operator negatively-controlled promoter, repressed by TetR and derepressed by the inducer tetracycline test for levels of expression during repressed versus derepressed state
	The quorum-sensing promoters: Plas and Plux as above
	The PlasOcI promoter-operator fusion negatively- and positively-controlled promoter in the final half adder design, repressed by cI and enhanced by LasR testfor activity in the repressed versus enhanced state test in addition to above construct since operator fusion may affect promoter activity

Mathematical Model

To create a predictive model, we used a set of differential equations to graph the approximate concentrations of each chemical with respect to time. These graphs are intended to illustrate the relative concentrations of the chemicals involved for each possible combination of inputs. The first quarter of the graph (t=0 to 500) illustrates the concentration of chemicals when adding 0+0; the second quarter (t=500 to 1000) illustrates the 0+1 case; the third quarter illustrates the 1+0 case; and the fourth quarter the 1+1 case.

File:UW Graphs.jpg

Measurements

Extensions

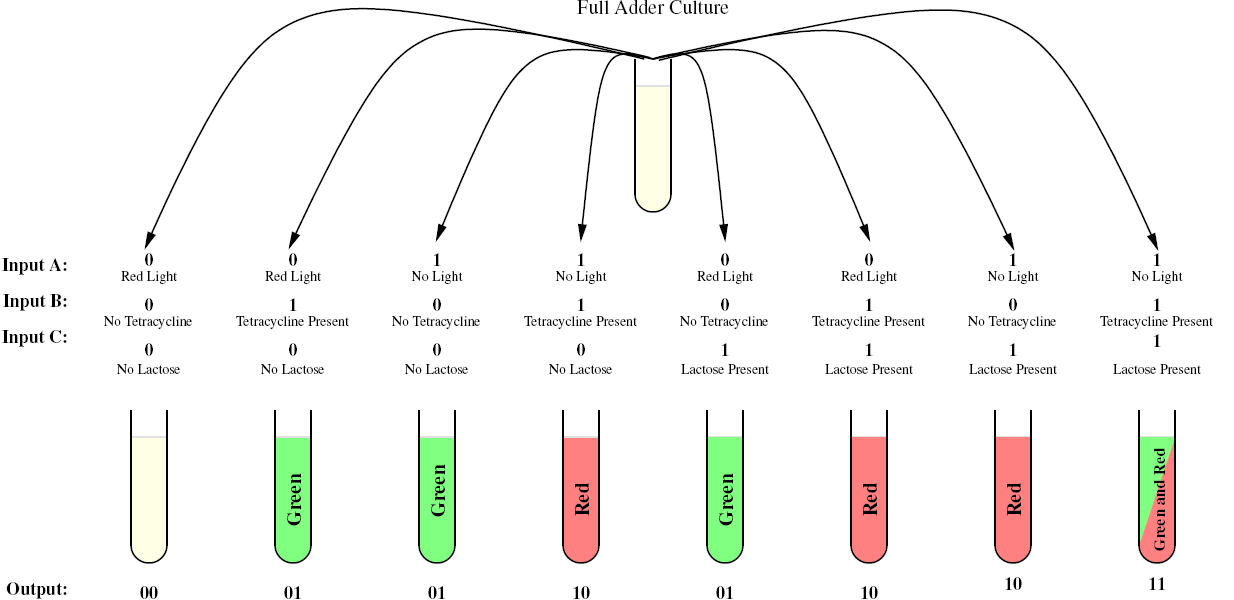
Full Adder

As a future project, we would like to extend our half-adder to a full-adder, which would be much more useful as it would give us the ability to add numbers of more than one digit. Below is a diagram of all the outputs given all possible inputs.

Inputs and Outputs of the Biological Full Adder

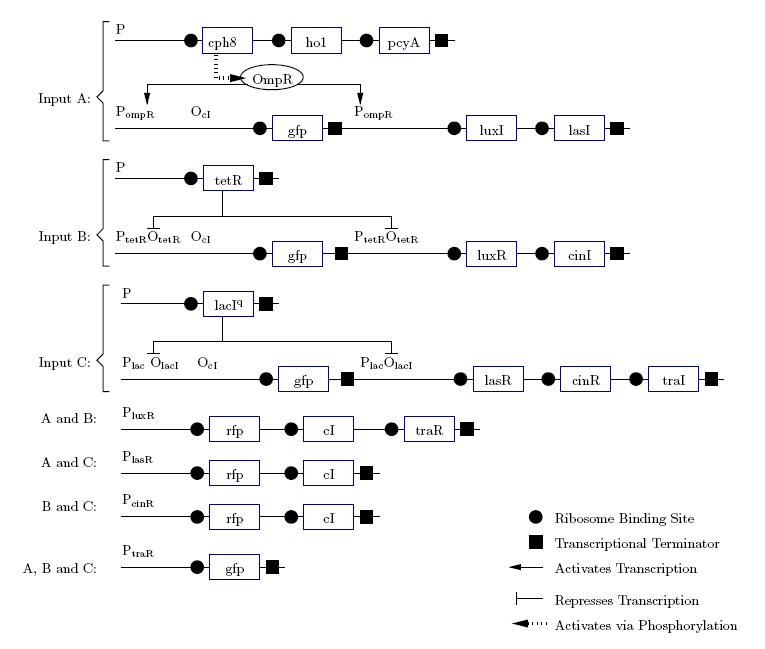
A gene design that makes use of some of the half-adder components can be seen below.

  Home