Glasgow/Modeling
From 2007.igem.org
| Line 4: | Line 4: | ||
|} | |} | ||
---- | ---- | ||
| - | [Trial model for the PDntR|S promoter] | + | [[Trial model for the PDntR|S promoter]] |
= Trial model for the PDntR|S promoter = | = Trial model for the PDntR|S promoter = | ||
Revision as of 20:50, 2 October 2007
| https://static.igem.org/mediawiki/2007/thumb/c/cc/Uog.jpg/50px-Uog.jpg | Back To Glasgow's Main Page |
|---|
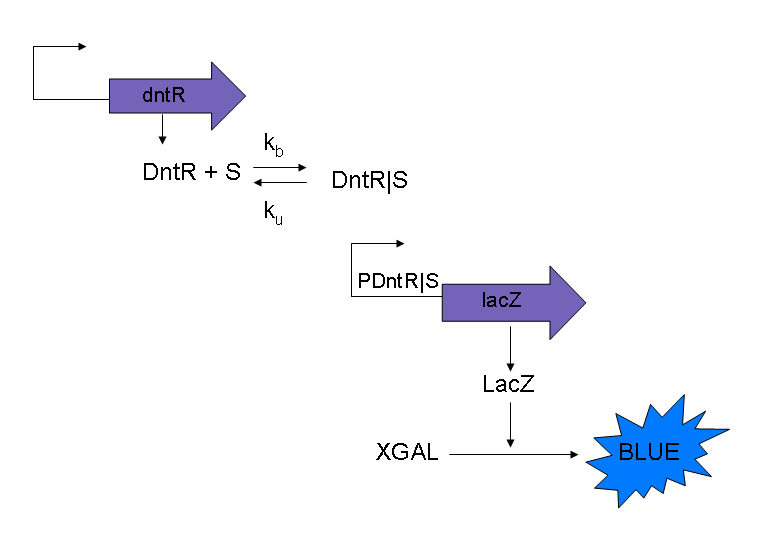
Trial model for the PDntR|S promoter
The current model that will be used for modeling purposes will use the three following equations to model the simple system as shown in Figure 1. The reasons for using these modified equations are discussed below.
Discussion
The equation for the change of DntR|S within the system could be modelled by Equation 4
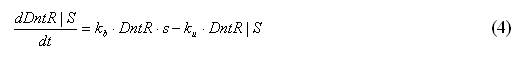
At the beginning of the reaction DntR will have an unknown constant value as it cannot be measured physically in the laboratory. As the DntR will have a constant value the DntR and kb can be replaced by another constant kb’ as shown
By substituting Equation 5 into Equation 4 gives

However it is clear from Equation 6 that as the signal increases the DntR|S will increase without ever reaching a saturation limit. It was decided that the equation should be changed to utilize Michaelis-Menten. This means that a saturation limit will now be possible as shown in Equation 1.
Next it is important to note that the signal equation includes a term for the degradation of the signal as this is possible in the physical model. This equation also includes a term for the binding and a term for the unbinding as shown in Equation 2.
Also it should be noted that in this model XGAL is ignored, this is because the level of blue that is measured is proportional to the LacZ produced. By ignoring XGAL it will simplify the system equations.
Another point to note is that in this model of the system the transcription and the translation steps have been ‘lumped’ together by using Michaelis-Menten rather than modeling these biological steps separately.