ETHZ/Intro Tim

From 2007.igem.org

(Difference between revisions)
(→'''.:: System Explanation ::.''')
(→'''.:: System Explanation ::.''')
Line 2: Line 2:
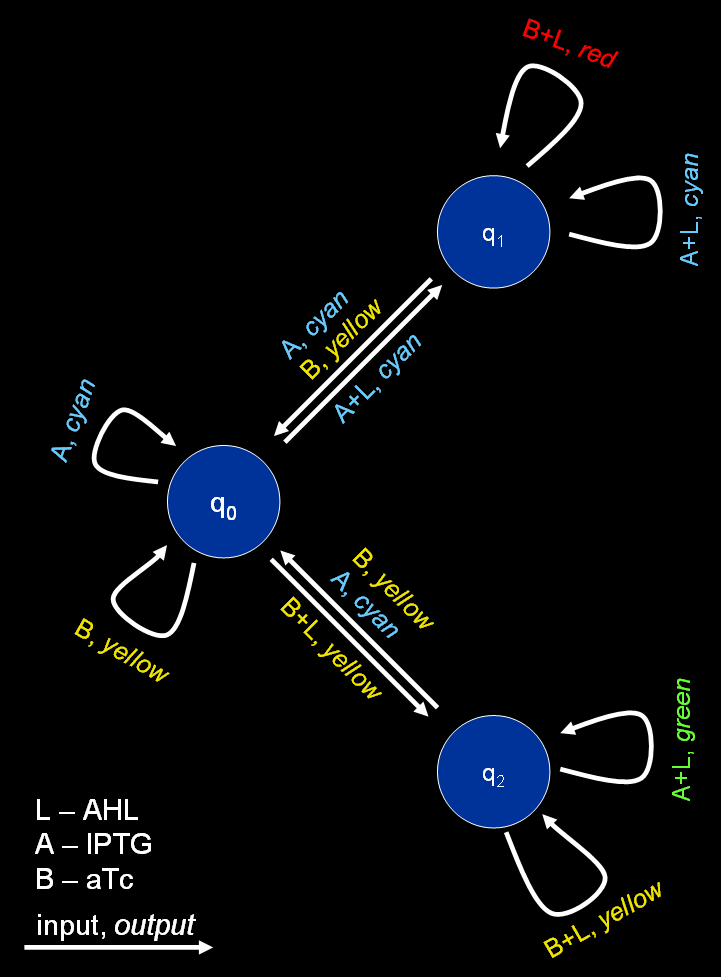
[[Image:FSM.png|thumb|450px|Figure 1: Graph representing the finite state machine.]]
[[Image:FSM.png|thumb|450px|Figure 1: Graph representing the finite state machine.]]
The proposed system is best described by a [http://en.wikipedia.org/wiki/Mealy_machine Mealy machine], a special type of [http://en.wikipedia.org/wiki/Finite_state_machine finite state machines] (FSM). Mealy machines are defined by a 6-tuple, (''Q'', ''q''<sub>0</sub>, Σ, Λ, ''δ'', ''Ω''), with:
The proposed system is best described by a [http://en.wikipedia.org/wiki/Mealy_machine Mealy machine], a special type of [http://en.wikipedia.org/wiki/Finite_state_machine finite state machines] (FSM). Mealy machines are defined by a 6-tuple, (''Q'', ''q''<sub>0</sub>, Σ, Λ, ''δ'', ''Ω''), with:
-
* ''Q'' - a set of states, for the proposed system we use five different states (''q''<sub>0</sub> - not yet trained, ''q''<sub>1</sub> - trained to recognize chemical A,  ''q''<sub>2</sub> - trained to recognize chemical B)
+
* ''Q'' - a set of states, for the proposed system we use three different states (''q''<sub>0</sub> - not yet trained, ''q''<sub>1</sub> - trained to recognize chemical A,  ''q''<sub>2</sub> - trained to recognize chemical B)
* ''q''<sub>0</sub> - a start state, here we assume we start in a state where the system is not yet trained
* ''q''<sub>0</sub> - a start state, here we assume we start in a state where the system is not yet trained
-
* Σ = {AL, A, BL, B} - an input alphabet
+
* Σ = {A+L, A, B+L, B} - an input alphabet
-
* Λ = {green, red, cyan, yellow, nothing} - an output alphabet
+
* Λ = {''green'', ''red'', ''blue'', ''yellow''} - an output alphabet
* ''δ'' : ''Q'' × Σ → ''Q'' - a state transition function
* ''δ'' : ''Q'' × Σ → ''Q'' - a state transition function
* ''Ω'' : ''Q'' × Σ → Λ - an output function
* ''Ω'' : ''Q'' × Σ → Λ - an output function
Line 15: Line 15:
! inputs/states !! ''q''<sub>0</sub> !! ''q''<sub>1</sub> !! ''q''<sub>2</sub>
! inputs/states !! ''q''<sub>0</sub> !! ''q''<sub>1</sub> !! ''q''<sub>2</sub>
|-
|-
-
! AL            || ''q''<sub>1</sub> || ''q''<sub>1</sub> || ''q''<sub>1</sub> ||
+
! A+L          || ''q''<sub>1</sub> || ''q''<sub>1</sub> || ''q''<sub>1</sub> ||
-
! AL            || nothing          || ||  
+
! A+L          || ''green''        || ''green''        || ''blue''
|-
|-
-
! A            || ''q''<sub>0</sub> || ''q''<sub>1</sub> || ''q''<sub>2</sub> ||
+
! A            || ''q''<sub>0</sub> || ''q''<sub>0</sub> || ''q''<sub>0</sub> ||
-
! A            || || red              || cyan
+
! A            || ''green''        || ''green''        || ''green''
|-
|-
-
! BL            || ''q''<sub>2</sub> || ''q''<sub>2</sub> || ''q''<sub>2</sub> ||
+
! B+L          || ''q''<sub>2</sub> || ''q''<sub>2</sub> || ''q''<sub>2</sub> ||
-
! BL            || nothing          || ||  
+
! B+L          || ''yellow''        || ''red''          || ''yellow'' 
|-
|-
-
! B            || ''q''<sub>0</sub> || ''q''<sub>1</sub> || ''q''<sub>2</sub> ||
+
! B            || ''q''<sub>0</sub> || ''q''<sub>0</sub> || ''q''<sub>0</sub> ||
-
! B            || || green        || yellow
+
! B            || ''yellow''        || ''yellow''        || ''yellow''
|-
|-
|}
|}
-
 
-
 
The resulting automaton is represented by Fig. 1.
The resulting automaton is represented by Fig. 1.

Revision as of 09:30, 18 October 2007

.:: System Explanation ::.

Figure 1: Graph representing the finite state machine.

The proposed system is best described by a [http://en.wikipedia.org/wiki/Mealy_machine Mealy machine], a special type of [http://en.wikipedia.org/wiki/Finite_state_machine finite state machines] (FSM). Mealy machines are defined by a 6-tuple, (Q, q0, Σ, Λ, δ, Ω), with:

  • Q - a set of states, for the proposed system we use three different states (q0 - not yet trained, q1 - trained to recognize chemical A, q2 - trained to recognize chemical B)
  • q0 - a start state, here we assume we start in a state where the system is not yet trained
  • Σ = {A+L, A, B+L, B} - an input alphabet
  • Λ = {green, red, blue, yellow} - an output alphabet
  • δ : Q × Σ → Q - a state transition function
  • Ω : Q × Σ → Λ - an output function

In detail, the transition function δ and the output function Ω look as follows:

inputs/states q0 q1 q2 inputs/states q0 q1 q2
A+L q1 q1 q1 A+L green green blue
A q0 q0 q0 A green green green
B+L q2 q2 q2 B+L yellow red yellow
B q0 q0 q0 B yellow yellow yellow

The resulting automaton is represented by Fig. 1.

Retrieved from "http://2007.igem.org/wiki/index.php/ETHZ/Intro_Tim"