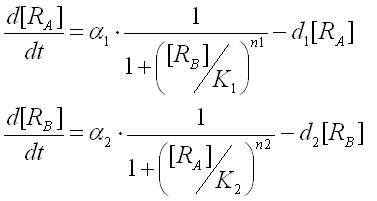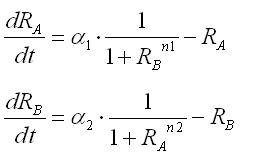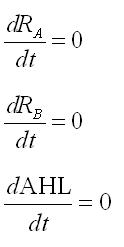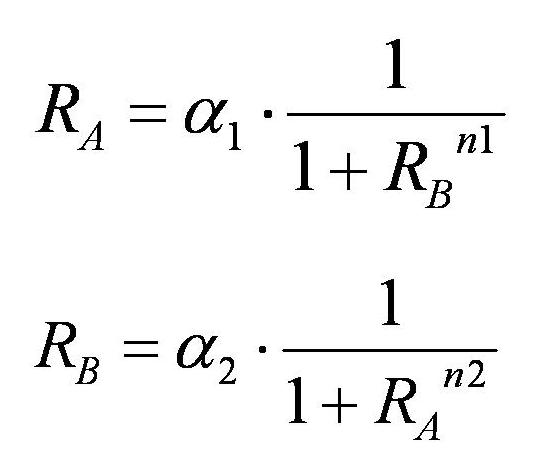Tokyo/Formulation/1.toggle model
From 2007.igem.org
(→1.toggle model) |
|||
| Line 1: | Line 1: | ||
== 1.toggle model == | == 1.toggle model == | ||
| - | First, | + | First,the ordinary differential equations(ODEs) of the toggle switch were derived as |
<br>[[Image:expression1-1.jpg|200px|]] [[Image:parameter1-1.jpg|200px|]] | <br>[[Image:expression1-1.jpg|200px|]] [[Image:parameter1-1.jpg|200px|]] | ||
| - | <br> | + | <br>These equations were normalized as follows: |
| - | + | ||
<br>[[Image:expression1-2.jpg|200px|]] | <br>[[Image:expression1-2.jpg|200px|]] | ||
| - | <br> | + | <br>In the steady state,time derivations are zero: |
| + | |||
| + | <br>[[Image:expression3-5.jpg|100px|]] | ||
| + | |||
| + | <br>As a result,the nullclines of this system were derived as | ||
<br>[[Image:Siki2.jpg|200px|]] | <br>[[Image:Siki2.jpg|200px|]] | ||
| - | <br> | + | <br>Therefore,the phase plane of this system can be plotted as Fig● |
<br>About parameters,we use three sets of parameters. | <br>About parameters,we use three sets of parameters. | ||
Revision as of 12:36, 23 October 2007
1.toggle model
First,the ordinary differential equations(ODEs) of the toggle switch were derived as
These equations were normalized as follows:
In the steady state,time derivations are zero:
As a result,the nullclines of this system were derived as
Therefore,the phase plane of this system can be plotted as Fig●
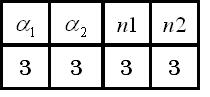
About parameters,we use three sets of parameters.
1)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.
2)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.
3)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.

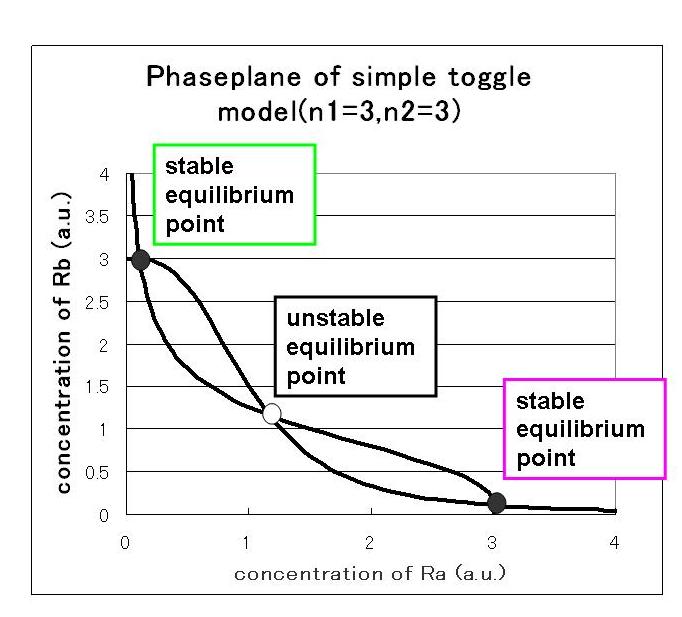
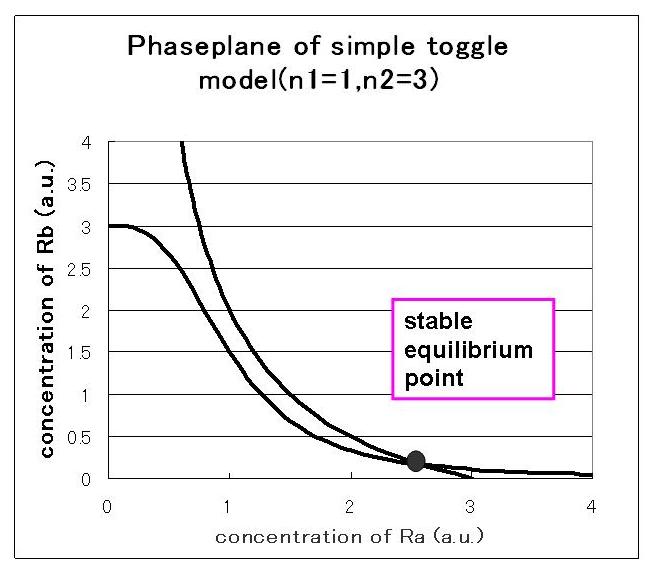
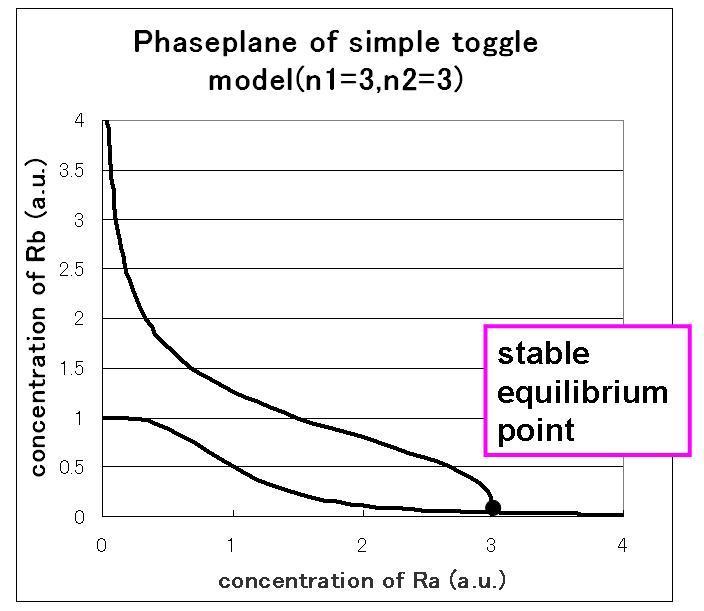
we correlate phaseplane analysis and simulation results.
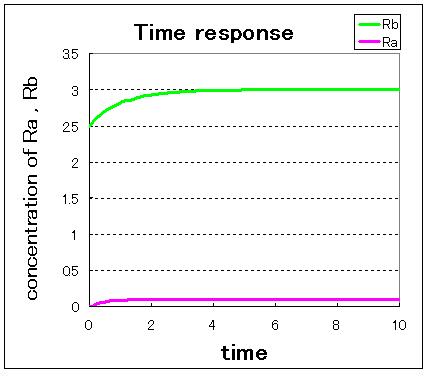
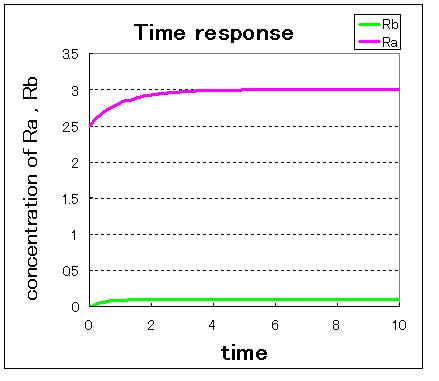
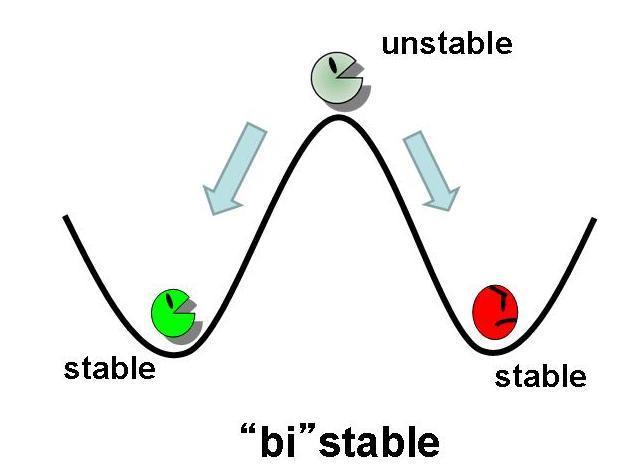
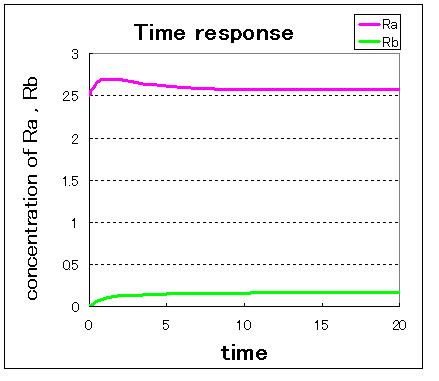
First,we simulate about the phaseplane of two stable equilibrium points(the upper left figure) and use three kinds of initial values.
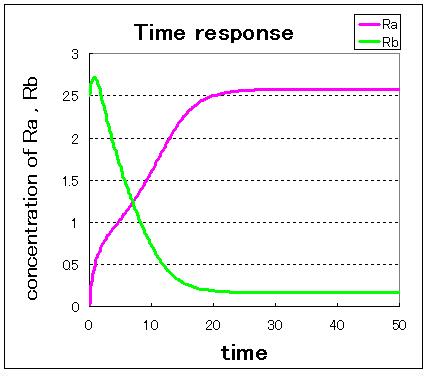
1. (Ra:low , Rb:high) 2. (Ra:high , Rb:low) 3. (Ra:middle , Rb:middle)
安定点B付近から始めるとB状態で安定し,安定点A付近から始めるとA状態で安定しているのが分かる.
不安定点付近から始めるとどちらかで安定化する.
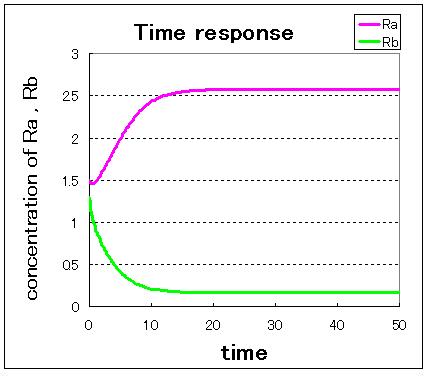
Next,
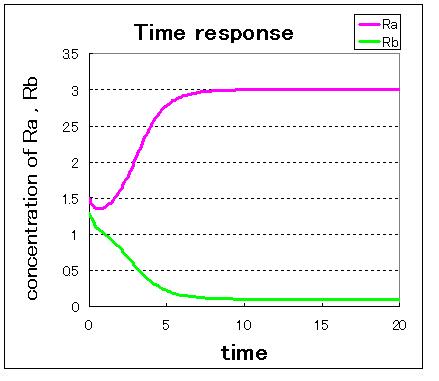
次に,安定点が一つしかない場合のシミュレーション結果は下のようになる.
安定点が一つしかない場合は,安定点B付近から始めてもA状態で安定化してしまうのが分かる.
As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.