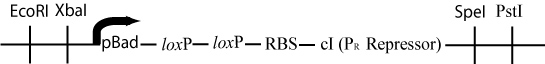Davidson Missouri W
From 2007.igem.org
(→'''Project Overview''') |
(→'''Project Overview''') |
||
| Line 80: | Line 80: | ||
[[Image:AdelmanGraph.JPG|thumb|300px|center| ]] | [[Image:AdelmanGraph.JPG|thumb|300px|center| ]] | ||
<br> | <br> | ||
| + | |||
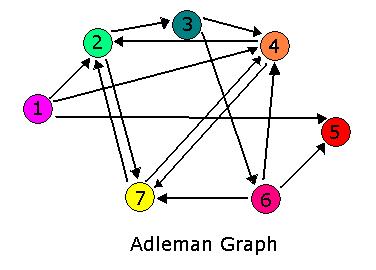
| + | The Adelman Graph with its seven vertices and fourteen arcs is too large to attack with our approach without first testing our procedures. To this end, Michelle and Jeff have been investigating induced subgraphs of the Adelman Graph. Ideally, we would like to partition the Adelman Graph into smaller graphs that could be constructed and tested individually, then linked together to form one large construct representing the Adelman Graph. It seems the most critical property of a good test graph is a unique Hamiltonian path. The smallest graph with a unique Hamiltonian path would be two vertices connected with a single edge. This is the one pancake problem worked on (and successfully achieved!) by the Davidson-Missouri Western team in 2006. The first non-trival (from a mathematical standpoint) graph would be a transitive directed graph on three vertices. The concept of transitivity is pervasive in many areas of mathematics. In the real numbers, the relation > is transitive. That is, if a>b and b>c, then we know that a>c. One example of a transitive induced graph of the Adelman graph is the subgraph on the vertices 1, 4, and 2. Notice that the edges of the Adelman Graph between these three vertices are precisely 14, 42, and 12. This construct, and others like it, have a unique Hamiltonian path AND have the property that there are no false positive results. This may provide a setting in which to test some of our proposed procedures. | ||
| + | |||
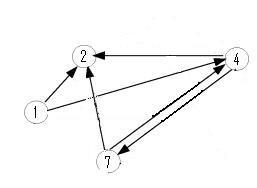
| + | Moving up a level, the graph below is nearly an induced subgraph of the Adelman Graph. (To be induced, it would require the arc 27 also be included, but to include this edge would destroy the property of having a unique Hamiltonian path.) This graph on four vertices with six edges provides a small example in which we can test our ability to biologically distinguish between true positives and false positives. There are 48 true positives for this graph (14, 47, 72 followed by the other three arcs in any order and any orientation). There are 42 false positives (14, 47, 74 followed by the other three arcs in any order but with at least one in forward orientation). | ||
[[Image:HamiltonInduced4.JPG|thumb|300px|center| ]] | [[Image:HamiltonInduced4.JPG|thumb|300px|center| ]] | ||
<br> | <br> | ||
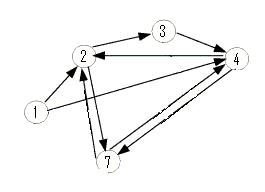
| - | + | The graph below is an induced subgraph of the Adelman Graph on five vertices with nine arcs. This graph has a unique Hamiltonian path AND contains the graph above. This might serve as a good intermediate on our way to the complete construction. Note also that this graph contains three transitive subgraphs (7,4,2), (4,7,2) and (1,4,2). Before jumping into constructions, we should carefully consider which coding sequence will correspond to each vertex of the Adelman Graph. If we are clever, it may be possible to piece together several smaller test constructs to efficiently create the full graph. Note: The counting of true positives and false positives for the graph below is non-trivial and in progress. | |
[[Image:HamiltonInduced5.JPG|thumb|300px|center| ]] | [[Image:HamiltonInduced5.JPG|thumb|300px|center| ]] | ||
Revision as of 14:34, 13 June 2007
===Davidson & Missouri Western Team Logos, iGEM2006===
Contents |
Team Meeting Notes
Western Meeting Notes 051407 to Present [1]
Students
• Will DeLoache, Junior Biology Major, [2]
• Oyinade Adefuye, Senior Biology Major, [3]
• Jim Dickson, Junior Math and Economics Major, [4]
• Amber Shoecraft, Math Major, [5]
• Andrew Martens, Senior Biology Major, [6]
• Michael Waters, Sophomore Biology Major, [7]
• Jordan Baumgardner, Junior Biology, Biochemistry/Molecular Biology Major, [8]
• Ryan Chilcoat, Junior Biology Major (Health Sciences), [9]
• Tom Crowley, Senior Biochemisty/Molecular Biology Major, [10]
• Lane H. Heard, Central High School graduate, [11]
• Nickolaus Morton, Junior Chemistry Major, [12]
• Michelle Ritter, Junior Mathematics Major, [13]
• Jessica Treece, Junior Biology Major (Health Sciences), [14]
• Matthew Unzicker, Senior Biochemistry/Molecular Biology Major, [15]
• Amanda Valencia, Senior Biochem/Molecular Biology Major, [16]
Faculty
• Malcolm Campbell [http://www.bio.davidson.edu/people/macampbell/macampbell.html], Professor, Department of Biology, [17]
• Karmella Haynes [http://www.bio.davidson.edu/people/kahaynes/kahaynes.html], Visiting Assistant Professor, Department of Biology, [18]
• Laurie Heyer [http://www.davidson.edu/math/heyer/], Associate Professor, Department of Mathematics, [19]
Shipping Address: Malcolm Campbell, Biology Dept. Davidson College, 209 Ridge Road, Davidson, NC 28036 [(704) 894-2692]
• Todd Eckdahl [http://staff.missouriwestern.edu/~eckdahl/], Professor, Department of Biology, [20]
• Jeff Poet [http://staff.missouriwestern.edu/~poet/], Assistant Professor, Department of Computer Science, Mathematics, and Physics, [21]
Shipping Address: Todd Eckdahl, Biology Department, Missouri Western State University, 4525 Downs Drive, Saint Joseph, MO, 64507 [(816) 271-5873]
Project Overview
Hamiltonian Path Problem As a part of iGEM2006, a combined team from Davidson College and Missouri Western State University reconstituted a hin/hix DNA recombination mechanism which exists in nature in Salmonella as standard biobricks for use in E. coli. The purpose of the 2006 combined team was to provide a proof of concept for a bacterial computer in using this mechanism to solve a variation of The Pancake Problem from Computer Science. This task utilized both biology and mathematics students and faculty from the two institutions.
For 2007, we continue our collaboration and our efforts to manipulate E. coli into mathematics problem solvers as we refine our efforts with the hin/hix mechanism to explore another mathematics problem, the Hamiltonian Path Problem. This problem was the subject of a groundbreaking paper by Adelman in 1994 (citation below) where a unique Hamiltonian path was found in vitro for a particular directed graph on seven nodes. We propose to make progress toward solving the particular problem in vivo.
The Adelman Graph with its seven vertices and fourteen arcs is too large to attack with our approach without first testing our procedures. To this end, Michelle and Jeff have been investigating induced subgraphs of the Adelman Graph. Ideally, we would like to partition the Adelman Graph into smaller graphs that could be constructed and tested individually, then linked together to form one large construct representing the Adelman Graph. It seems the most critical property of a good test graph is a unique Hamiltonian path. The smallest graph with a unique Hamiltonian path would be two vertices connected with a single edge. This is the one pancake problem worked on (and successfully achieved!) by the Davidson-Missouri Western team in 2006. The first non-trival (from a mathematical standpoint) graph would be a transitive directed graph on three vertices. The concept of transitivity is pervasive in many areas of mathematics. In the real numbers, the relation > is transitive. That is, if a>b and b>c, then we know that a>c. One example of a transitive induced graph of the Adelman graph is the subgraph on the vertices 1, 4, and 2. Notice that the edges of the Adelman Graph between these three vertices are precisely 14, 42, and 12. This construct, and others like it, have a unique Hamiltonian path AND have the property that there are no false positive results. This may provide a setting in which to test some of our proposed procedures.
Moving up a level, the graph below is nearly an induced subgraph of the Adelman Graph. (To be induced, it would require the arc 27 also be included, but to include this edge would destroy the property of having a unique Hamiltonian path.) This graph on four vertices with six edges provides a small example in which we can test our ability to biologically distinguish between true positives and false positives. There are 48 true positives for this graph (14, 47, 72 followed by the other three arcs in any order and any orientation). There are 42 false positives (14, 47, 74 followed by the other three arcs in any order but with at least one in forward orientation).
The graph below is an induced subgraph of the Adelman Graph on five vertices with nine arcs. This graph has a unique Hamiltonian path AND contains the graph above. This might serve as a good intermediate on our way to the complete construction. Note also that this graph contains three transitive subgraphs (7,4,2), (4,7,2) and (1,4,2). Before jumping into constructions, we should carefully consider which coding sequence will correspond to each vertex of the Adelman Graph. If we are clever, it may be possible to piece together several smaller test constructs to efficiently create the full graph. Note: The counting of true positives and false positives for the graph below is non-trivial and in progress.
Proposed Construct with Cre/loxP
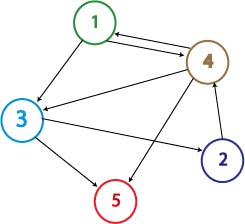
In order to determine if a Hamiltonian Path exists in the directed graph above, we propose a plasmid design similar to that shown below:
This cartoon represents a solved arangement of our proposed construct. Between the two pairs of BioBrick restriction enzyme sites lies a region containing eight flippable DNA fragments, each flanked by hixC sites (represented by the black, jagged rectangles). Each node of the graph represents one of the following genes: GFP (Green Fluorescent Protein), Kanamycin Resistance, cre, pir200, and a transcription terminator. Each edge of the graph is included in the construct between two hixC sites. In the presence of Hin protein, flipping of the edges at hixC sites will produce random walks through the graph. When flipped into the correct orientation and located upstream of any transcription terminators, a given gene will be transcribed (denoted by a bold outline in the cartoon above). In the solved arrangement shown above, a Hamiltonian Path is determined to exist in the graph because all genes are expressed, and no extra edges exist in the coding region. Extra edges in the coding region can be detected by gel electrophoresis.
The four reporter genes used in the construct above will produce three distinct phenotypes when in the solved orientation. GFP will cause the E. Coli cells to glow green, Kanamycin resistance will allow the cells to grow in the presence of the antibiotic, Kanamycin, and cre and pir200 will cause the entire DNA region between the two loxP sites to be excised into a separate plasmid and amplified. When the cre gene is in the solved orientation, it produces the Cre protein. It has been demonstrated that Cre can bind to two separated loxP sites and excise the DNA in the middle, forming a new plasmid [http://www.ncbi.nlm.nih.gov/sites/entrez?cmd=Retrieve&db=PubMed&list_uids=9526700&dopt=Abstract]. If Cre was produced, then the plasmid above would be cut at its loxP sites, and produce the two plasmids shown below.
The DNA fragment located between the two loxP sites has now been excised and formed into a new plasmid. The E. Coli cell has essentially spit out the answer to the Hamiltonian Path Problem on a separate plasmid that can be easily isolated. This solved plasmid is resistant to kanamycin (due to the solved orientation of the kanamycin resistance gene) and contains the gamma-ori origin of replication. It has been shown that pi-protein (transcribed by the pir200 gene) initiates amplification of plasmids with the gamma-ori origin of replication [http://www.ncbi.nlm.nih.gov/sites/entrez?cmd=Retrieve&db=PubMed&list_uids=9526700&dopt=Abstract]. Therefore, only when the pir200 gene is in the solved orientation will the excised plasmid will be amplified.
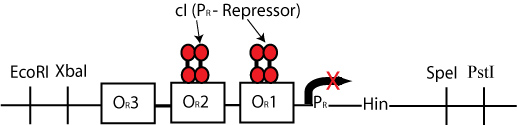
The original plasmid has now lost all of the DNA between the two loxP sites. The pBad promoter (upstream of the first loxP site) has been moved just upstream of the ribsosomal binding site and the cI gene (downstream of the second loxP site). This rearrangement will cause the transcription of cI, a gene that represses the Cro promoter -P(R)- in lamda phage by binding to the first and second operator regions (Ptashne, 2004).
By constructing a plasmid whose transcription of Hin is dependent on promotion from the P(R) promoter, in the manner shown below, we can terminate the transcription of Hin (and the flipping of hixC sites) whenever a plasmid is excised from the original construct to produce cI transcription.
The plasmid containing Hin will have resistance to a different antibiotic than the original construct plasmid or the excised plasmid (Chloramphenicol for instance) and would have a similar design to the cartoon above.
Once pBad is joined with the RBS and cI gene in the original plasmid, transcription of cI would occur, and transcription of Hin would be repressed. This would be a mechanism for stopping Hin-induced flipping once a solution had been found.
In order to build the proposed construct, a hixC site must be inserted into each reporter gene. Our lab has already successfully inserted hixC into GFP, retaining its functionality [http://www.bio.davidson.edu/Courses/Immunology/Students/spring2006/Acker/Acker_finalpaperGFP.doc]. We have also found literature on the successful splitting of the cre gene [http://www3.interscience.wiley.com/cgi-bin/abstract/104558885/ABSTRACT?CRETRY=1&SRETRY=0].
Resources / Citations
Missouri Western's Wet Lab Protocols
[http://gcat.davidson.edu/iGEM07/genesplitter.html Spliting Genes Web Tool]
Cool site for Breakfast [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml]
Karen Acker's paper describing GFP and TetA(c) with Hix insertions [http://www.bio.davidson.edu/Courses/Immunology/Students/spring2006/Acker/Acker_finalpaperGFP.doc]
Bruce Henschen's paper describing one-time flippable Hix sites [http://www.bio.davidson.edu/Courses/genomics/2006/henschen/Bruce_Finalpaper.doc]
Intro to Hamiltonian Path Problem and DNA [http://www.ams.org/featurecolumn/archive/dna-abc2.html]
Adelman, LM. Molecular Computation of Solutions To Combinatorial Problems. Science. 11 November 1994. Vol. 266. no. 5187, pp. 1021 - 1024
Ptashne, Mark. A Genetic Switch: Phage Lambda Revisited, Third Edition. New York. Cold Spring Harbor Laboratory Press: 2004.
Literature and Registry Research
Registry Search for Possible Promoters:
BBa_J24669 --- arabinose induced
BBa_R0082 --- Is upstream of the ompC porin gene
BBa_R0074 --- Penl regulated
BBa_I14017 --- P(Rhl)
BBa_I14018 --- P (Bla) --> amp resistance
BBa_J3902 --- Pr Fe (Pl + Pll rus operon)
BBa_R0077 --- CinR --> thought to have own terminator
BBa_R0078 --- CinR (no RBS)
BBa_R0062 --- luxR & HSL regulated -- luxpR
Possibly the use of Constitutive Promoter Family Members to strengthen other promoters.
Literature Search for Polycistronic Genes on Plasmids
Sol Operon http://www.jstage.jst.go.jp/article/bbb/71/1/58/_pdf
Transfer (tra) Operon http://www.pubmedcentral.nig.gov/picrender.fcgi?artid=1347297&blobtype=pdf
Oligopeptide Permease (opp) http://www.pubmedcentral.nig.gov/picrender.fcgi?artid=1087318&blobtype=pdf