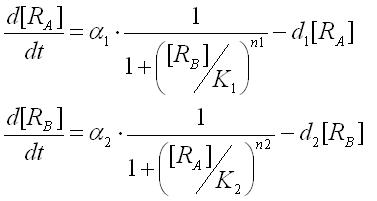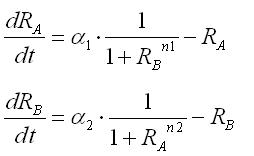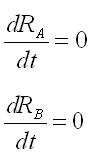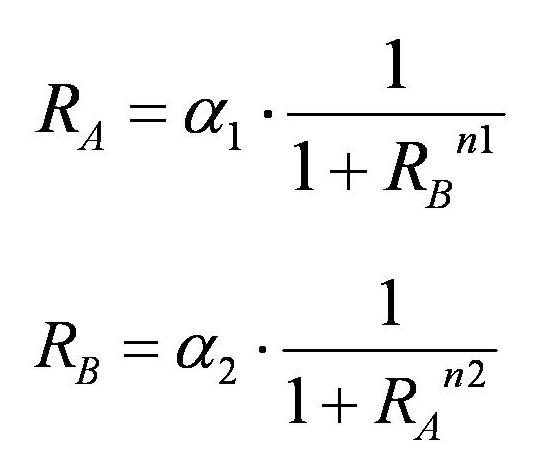Tokyo/Formulation/1.toggle model

From 2007.igem.org

(Difference between revisions)
Line 2: Line 2:
First,the ordinary differential equations(ODEs) of the toggle switch were derived as
First,the ordinary differential equations(ODEs) of the toggle switch were derived as
-
<br>[[Image:expression1-1.jpg|200px|]]  [[Image:parameter1-1.jpg|200px|]]  
+
<br>[[Image:expression1-1.jpg|200px|left|thumb|Ex1-1]]  [[Image:parameter1-1.jpg|200px|]]  
<br>These equations were normalized as follows:
<br>These equations were normalized as follows:
-
<br>[[Image:expression1-2.jpg|200px|]]
+
<br>[[Image:expression1-2.jpg|200px|none|thumb|Ex1-2]]
<br>In the steady state,time derivatives are zero:
<br>In the steady state,time derivatives are zero:
-
<br>[[Image:expression3-5.jpg|100px|]]
+
<br>[[Image:expression1-3.jpg|80px|none|thumb|Ex1-3]]
<br>As a result,the nullclines of this system were derived as
<br>As a result,the nullclines of this system were derived as
-
<br>[[Image:Siki2.jpg|200px|]]
+
<br>[[Image:Siki2.jpg|200px|none|thumb|Ex1-4]]
-
<br>which indicate the nullclines of the system shown in Fig●．
+
<br>which indicate the nullclines of the system shown in Fig 1.A-C.c.Where about parameters,we use three sets of parameters.
-
<br>About parameters,we use three sets of parameters.
+
-
<br>　　1)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.
+
-
<br>　　2)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.
+
-
<br>　　3)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.
+
-
<br>[[Image:parameter1-2.jpg|150px|]][[Image:parameter1-3.JPG|150px|]][[Image:parameter1-4.JPG|150px|]]
+
-
<br>[[Image:toggle1.jpg|303px|]][[Image:toggle2.jpg|300px|]][[Image:Toggle1-4.jpg |300px|]]
+
-
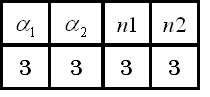
<br>First,we carried out kinetic simulations in the condition of Fig●.The results are shown in Fig●.
+
<br>　　A)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.
 +
<br>[[Image:parameter1-2.jpg|150px|center|thumb|Tble1.A]]
 +
<br>　　B)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.
 +
<br>[[Image:parameter1-3.JPG|150px|center|thumb|Table1.B]]
 +
<br>　　C)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.
 +
<br>[[Image:parameter1-4.JPG|150px|center|thumb|Table1.C]]
-
<br>  1. (Ra:low , Rb:high) 2. (Ra:high , Rb:low) 3. (Ra:middle , Rb:middle)
+
[[Image:toggle1.jpg|260px|left|thumb|Figure 1.A]]
 +
[[Image:toggle2.jpg|270px|left|thumb|Figure 1.B]]
 +
[[Image:Toggle1-4.jpg|270px|none|thumb|Figure 1.C]]
 +
<br>First,we carried out kinetic simulations in the condition of Fig1.A. The results are shown in Fig2.A-C.
-
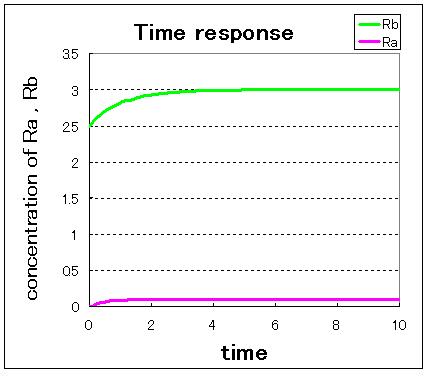
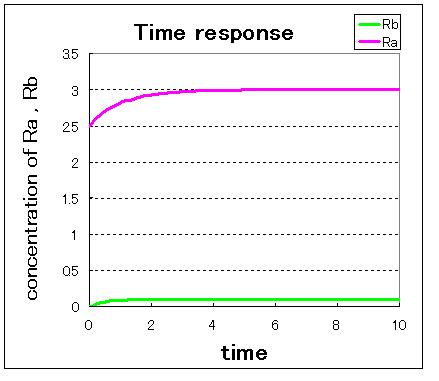
<br>[[Image:toggle3.jpg|200px|]] [[Image:toggle4.JPG|200px|]] [[Image:toggle5.JPG|200px|]][[Image:toggle1-1.jpg|200px|]]
+
[[Image:toggle3.jpg|200px|left|thumb|Figure 2.A  (Ra(0),Rb(0))=(0.0,2.5)]] [[Image:toggle4.JPG|200px|left|thumb|Figure 2.B  (Ra(0),Rb(0))=(2.5,0.0)]]
 +
[[Image:toggle5.JPG|200px|left|thumb|Figure 2.C  (Ra(0),Rb(0))=(1.5,1.3)]]
 +
[[Image:toggle1-1.jpg|200px|none|thumb|Figure 3  two stable]]
-
<br>Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5),which is near stable equilibrium point B, the values of Ra and Rb goes to stable equilibrium point B and when the initial condition is (Ra,Rb)=(2.5,0.0),which is near stable equilibrium point A, the values of Ra and Rb goes to stable equilibrium point B.
 
-
<br>Next,when the number of stable equilibrium point is one, the result of simulation are shown in Fig●
+
<br>Fig 2.A-C indicate that when the initial condition is (Ra,Rb)=(0.0,2.5),which is near stable equilibrium point B, the values of Ra and Rb goes to stable equilibrium point B and when the initial condition is (Ra,Rb)=(2.5,0.0),which is near stable equilibrium point A, the values of Ra and Rb goes to stable equilibrium point B.
-
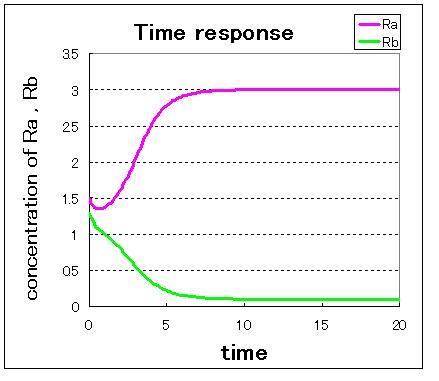
<br>[[Image:toggle6.JPG|200px|]] [[Image:Toggle7.JPG|200px|]] [[Image:toggle8.JPG|200px|]][[Image:toggle1-2.jpg|200px|]]
+
<br>Next,when the number of stable equilibrium point is one, the result of simulation are shown in Fig 1.B.  
<br>Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5) and when the initial condition is (Ra,Rb)=(2.5,0.0), the values of Ra and Rb goes to stable equilibrium point B.
<br>Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5) and when the initial condition is (Ra,Rb)=(2.5,0.0), the values of Ra and Rb goes to stable equilibrium point B.
<br>'''As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.'''
<br>'''As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.'''

Revision as of 04:36, 24 October 2007

1.toggle model

First,the ordinary differential equations(ODEs) of the toggle switch were derived as


Ex1-1
Parameter1-1.jpg


These equations were normalized as follows:


Ex1-2


In the steady state,time derivatives are zero:


Ex1-3


As a result,the nullclines of this system were derived as


Ex1-4


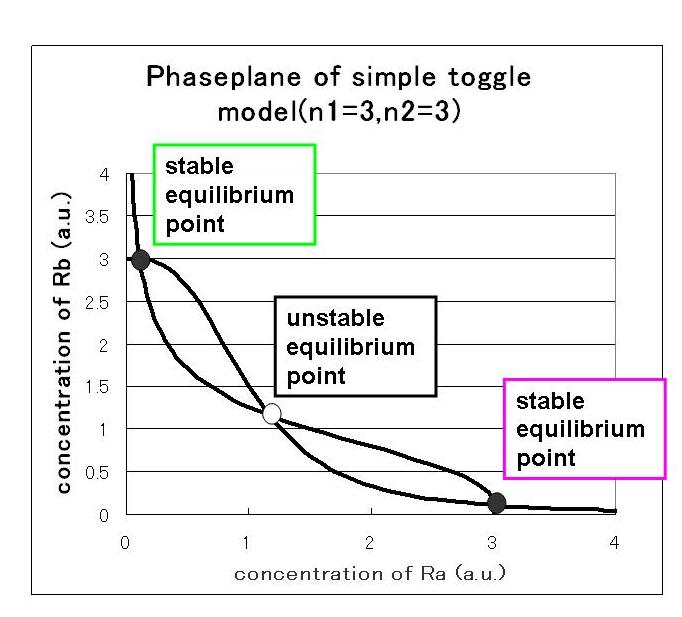
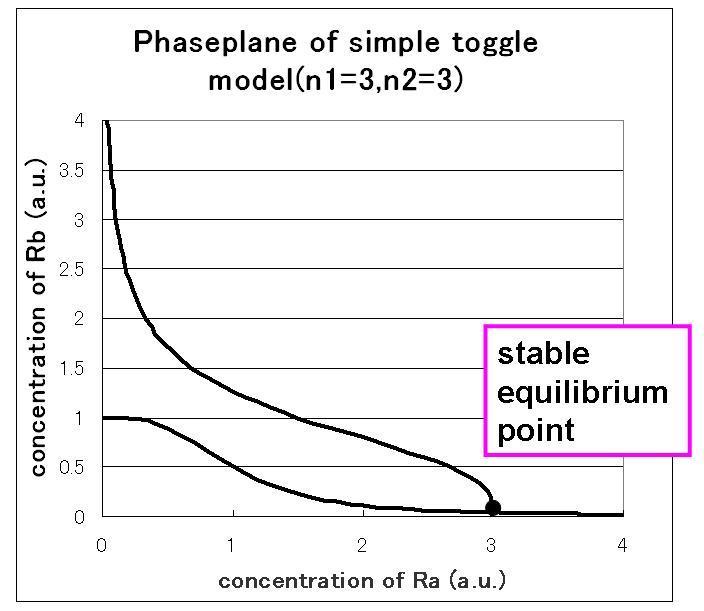
which indicate the nullclines of the system shown in Fig 1.A-C.c.Where about parameters,we use three sets of parameters.


　　A)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.


Tble1.A


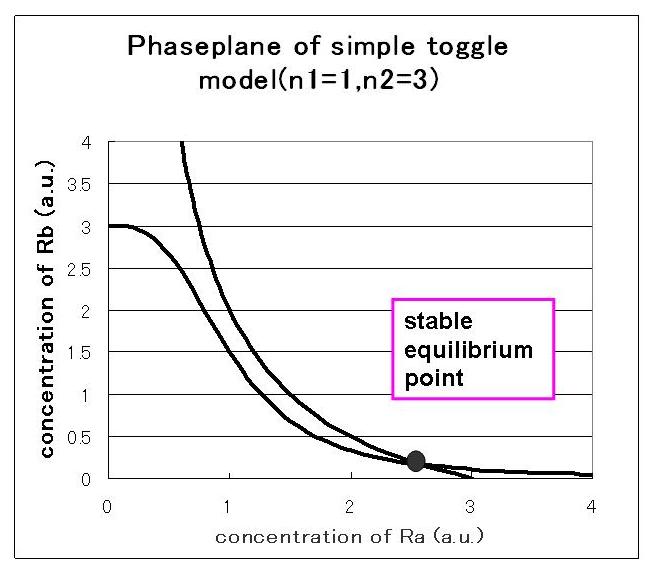
　　B)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.


Table1.B


　　C)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.


Table1.C
Figure 1.A
Figure 1.B
Figure 1.C


First,we carried out kinetic simulations in the condition of Fig1.A. The results are shown in Fig2.A-C.

Figure 2.A (Ra(0),Rb(0))=(0.0,2.5)
Figure 2.B (Ra(0),Rb(0))=(2.5,0.0)
Figure 2.C (Ra(0),Rb(0))=(1.5,1.3)
Figure 3 two stable



Fig 2.A-C indicate that when the initial condition is (Ra,Rb)=(0.0,2.5),which is near stable equilibrium point B, the values of Ra and Rb goes to stable equilibrium point B and when the initial condition is (Ra,Rb)=(2.5,0.0),which is near stable equilibrium point A, the values of Ra and Rb goes to stable equilibrium point B.


Next,when the number of stable equilibrium point is one, the result of simulation are shown in Fig 1.B.


Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5) and when the initial condition is (Ra,Rb)=(2.5,0.0), the values of Ra and Rb goes to stable equilibrium point B.


As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.

Retrieved from "http://2007.igem.org/wiki/index.php/Tokyo/Formulation/1.toggle_model"