From 2007.igem.org

Revision as of 16:55, 25 October 2007

• Main Page
• Introduction
• Design Process
• Modeling
• Construction Process
• Results
• Perspectives
• Acknowledgments

In this part of our work, we aim at characterizing the diffusion of the DAP and the effect on the cells differentiation. This study consists in observing by simulation, the diffusion of DAP in a lawn of germ cells with some isolated somatic cells using a cellular automaton.

Introduction

DAP feeding between somatic and germ cells is based on an indirect communication process: soma cells produce DAP and release it in the environment; DAP molecules freely diffuse outside until they are captured by a germ cell. We are interesting here in the case where the differentiation of a germ into a soma is DAP dependent. In order to figure out the relation between DAP diffusion and differentiation we propose a simple cellular automaton on square grid. Each cell of the automaton contains a bacterium. We first detail some hypotheses used in this model, then we specify the local behavior rules following by each automaton cell. Finally, the generated simulation is presented.

Hypotheses

The chosen approach consists in observing the DAP diffusion and differentiation frontwaves. In order to focus on these phenomenon, we work on a constant population (no death, no division). So we assume that without DAP in its surrounding, a germ cell does not die but remain in passive state (we can imagine that they are at a stationary phase or between to division cycle). It will seem that DAP wake up bacteria but it's just an artifact due to this assumption.

It may happen that a germ cell as enough DAP to evolve (typically when it is touched by a DAP diffusion front) but we assume that the contribution is not enough for the cell to divide.

Finally, we assume then that DAP is produced in somatic cells only and consumed by germ cells. The communication is done by distinguishing in the automaton intra and extra cellular DAP (respectively named DAPi and DAPe).

Model Description

In this we focus on the elaboration of the cellular automaton.

Structure

As we have previously announced, we design cellular automaton on a square grid. More precisely, in order to avoid boundary effects, we assume that the grid is actually wrapped in such a way the grid topology is a 2D torus. Each cell of the automaton contains a bacterium, either germ or somatic, together with the external DAP concentration. So we represent the different states of the automaton cell by tuple of values {DAPe,DAPi,Type}:

• DAPe is the external DAP concentration,

• DAPi is the internal DAP concentration in the bacterium,

• Type represent if the bacterium is differntiated or not; it can take two values BactG and BactS.

Dynamics

The following rules specify the local evolution of each cell of the automaton. We distinguished to evolution laws depending on what kind of bacterium is in the cell:

• In the case of a BactS cell: we have to consider the diffusion of DAPe between the considered cell and its neighbors, the export of DAP from the inside to the outside, and finally the production of DAPi. The rule can be presented as follows:

 DAPe <- DAPe + (DAPe diffused in the neighborhood) + (DAPi lost by export)
 DAPi <- DAPi + (DAPi produced) - (DAPi lost by export)
 Type <- BactS

• In the case of a BactG cell: we have to consider the diffusion of DAPe between the considered cell and its neighbors, the import of DAP from the outside to the inside, the consumption of DAPi, and finally the differentiation when DAP concentration reaches a right range of values. The rule can be presented as follows:

 DAPe <- DAPe + (DAPe diffused in the neighborhood) - (DAPi gain by import)
 DAPi <- DAPi - (DAPi consumed) + (DAPi gain by import)
 Type <- if (min_threshold) < DAPi < (max_threshold) then BactS else BactG

Initial state

Our initial state is 30x30 2D toric cellular automaton where all cells are initialized by value {DAPe=0,DAPi=0,Type=BactG} but four {DAPe=0,DAPi=0,Type=BactS} are randomly placed in the grid.

Output

We use gbview to generate those pictures

The output is two animated pictures one show the differentiation the other the diffusion of DAPe

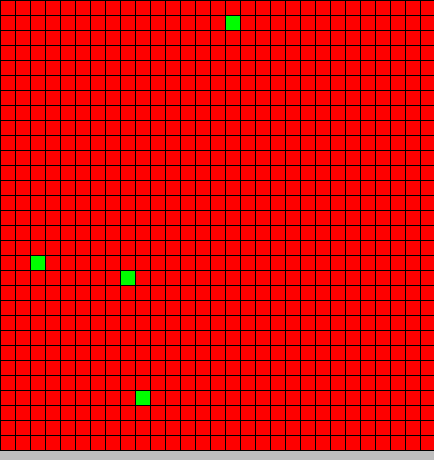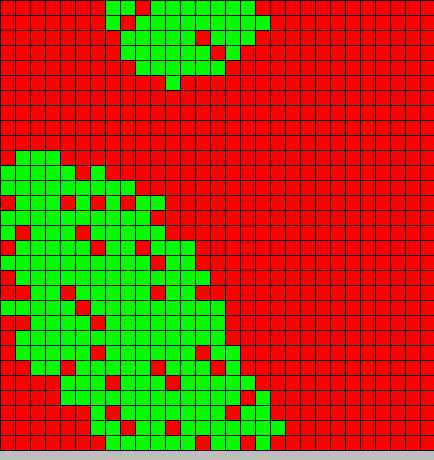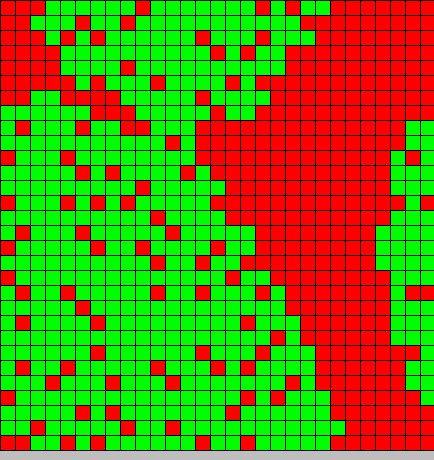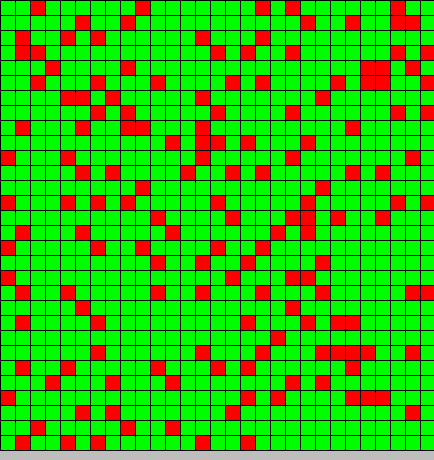
• The first picture show the diffusion of DAP

We can see a front wave in light blue after that there is a dark blue area in which the systeme is stable the concentration doesn't evolve.

• The second picture show the differentiation

Red BactG

Green BactS

The differentiation follow the wave front

In reality this phenomenon does not exist, but this model show that the low concentration of DAP induces differentiation (cells become green)(dark blue),then with high concentration of DAP, the differentiation is inhibited. That why some cells stay in red
We can also note that the population can be stabilized, and the level of DAP remains constant in these areas, the color of the cells doesn't change anymore and the concentration of DAP doesn't change too.

After playing with the parameters, we can deduct 2 important things:

• The inhibition most be strong and effective (we play with the minimal and maximal value of DAP for differentiation)

if it isn't the case the system collapse all the bactG stay BactG if the inhibition is too strong or switch to BactS if the inhibition is not enough strong.

• The production and diffusion of DAP will be a critical factor

The DAP has to be produce then he will be exported, it will diffuse in the medium and will be imported

There is no proof of a special system to import or export DAP, so for each step there is a large amount of DAP lost.

Sources