Davidson Missouri W/Solving the HPP in vivo
From 2007.igem.org
Using the Hin/hixC flipping mechanism, we are developing a bacterial computer which solves a specific mathematical problem, the Hamiltonian Path problem.
Contents |
The Hamiltonian Path Problem
A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point and an endpoint, does it contain a Hamiltonian path?
We solve our problem by transforming E. coli cells with specially engineered plasmids.
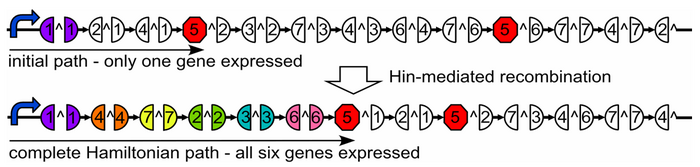
Designing a Plasmid
Our plasmid consists of reporter genes and hixC sites. hixC sites are placed within the coding regions of our reporter genes. The reporter genes are joined in such a way as to represent a graph. Each reporter gene represents a node, and the connection of two reporter genes together without any hixC sites in between represents an edge.
Such a plasmid design allows us to flip the edges of the graph into all possible permutations. Each permutation represents a potential path through the graph; permutations with all the proper phenotypes can be selected for. This system therefore allows for the detection of computation, as solutions to the Hamiltonian Path problem will manifest themselves via the reporter genes.
Developing Nodes
We represent the graph's nodes with reporter genes. In order to allow for flipping, we must insert hixC sites within the coding regions of our reporter genes. We call this process gene splitting. The central issue with gene splitting is that an additional 13 amino acids are added within the resulting protein. If our reporter gene tolerates a hixC insertion, and still functions as a reporter properly, then we can use it as a node on our graph.
Detecting a Solution
The primary method for seeing if there is a solution is by screening for all correct phenotypes. For example, if some cells do not have antibiotic resistance, or if they do not exhibit a particular color, then we know they have not computed a solution to the problem. However, there exists the possibility of a false-positive solution. In this case, all genes have their second portion immediately following their first. Yet the resulting path will be illogical: it will contain a "teleportation," which means that, in order to travel the path, it would be necessary to move between two nodes without following an edge.
The potential for false-positives thus requires another way of verifying solutions. The length of a solution, in terms of base-pairs, is always known. It is the sum of the lengths of all split genes. Furthermore, the first and last nodes are constant, as the first one is not flippable and the last node is the transcriptional terminator. These facts mean that PCR can be used to verify solutions. Primers can be designed from the first and last node, and running PCR products on a gel will give the lengths of the amplified DNA. If any segment has the correct length then we know there is a solution.