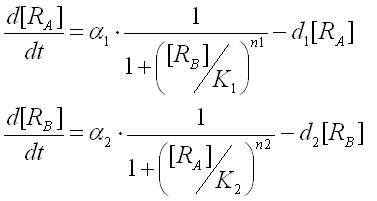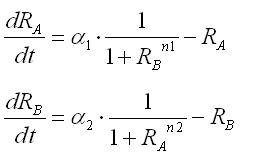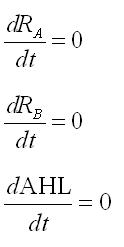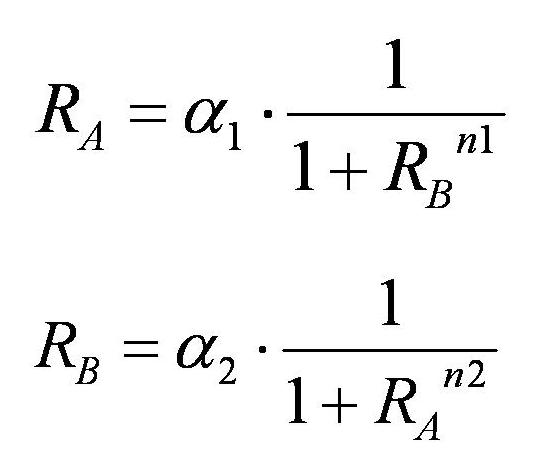From 2007.igem.org

1.toggle model

First,the ordinary differential equations(ODEs) of the toggle switch were derived as

These equations were normalized as follows:

In the steady state,time derivatives are zero:

As a result,the nullclines of this system were derived as

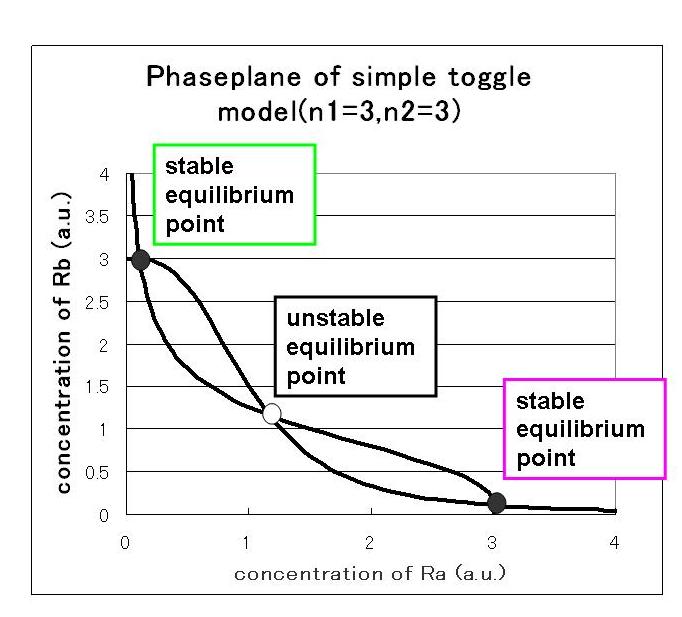
which indicate the nullclines of the system shown in Fig●．
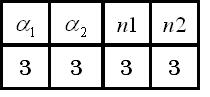
About parameters,we use three sets of parameters.
　　1)the maximum expression rate of repressor A and repressor B is balanced,and hill coefficient of both A and B is three.
　　2)the maximum expression rate of repressor A and repressor B is equal,and hill coefficient of A is one.
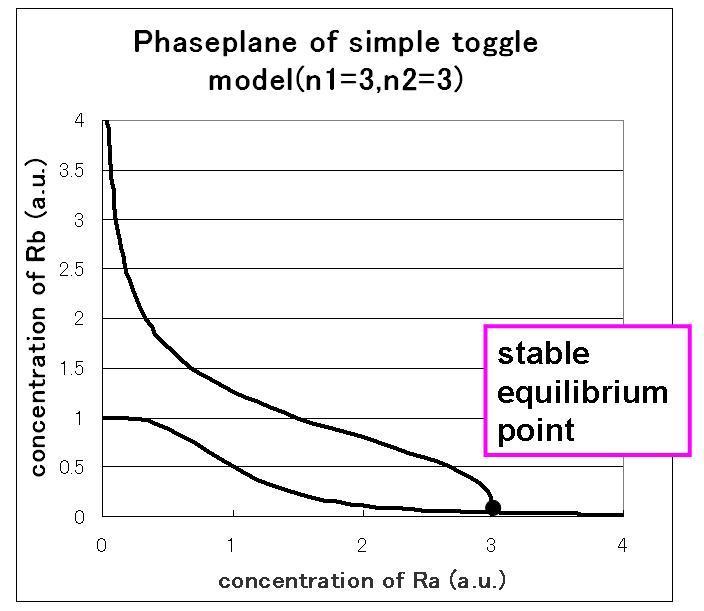
　　3)the maximum expression rate of repressor A and repressor B is not balanced,and hill coefficient of both A and B is three.

First,we carried out kinetic simulations in the condition of Fig●.The results are shown in Fig●.

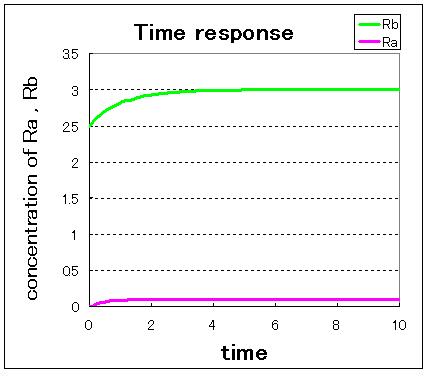
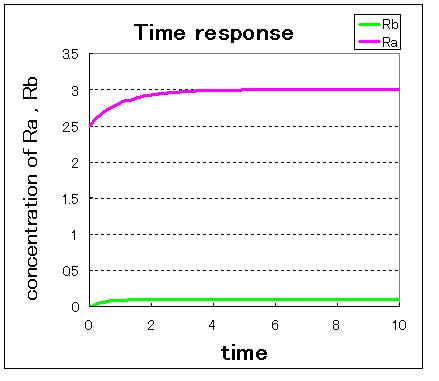
1. (Ra:low , Rb:high) 2. (Ra:high , Rb:low) 3. (Ra:middle , Rb:middle)

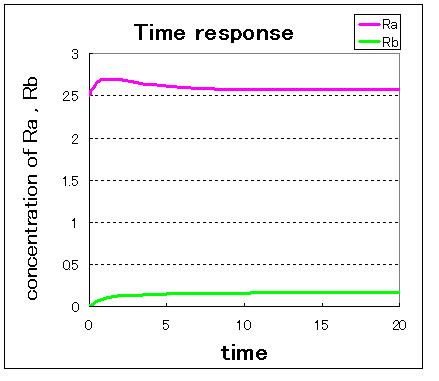
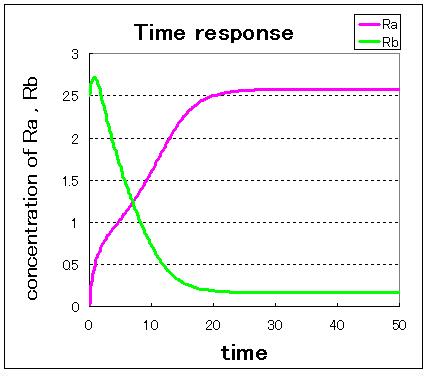
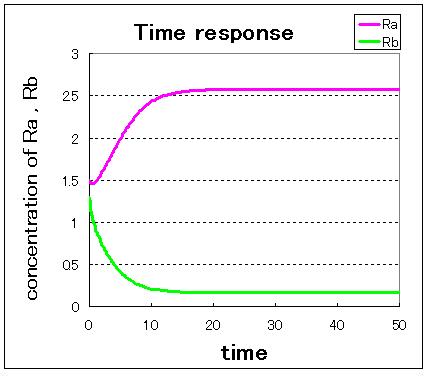
Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5),which is near stable equilibrium point B, the values of Ra and Rb goes to stable equilibrium point B and when the initial condition is (Ra,Rb)=(2.5,0.0),which is near stable equilibrium point A, the values of Ra and Rb goes to stable equilibrium point B.

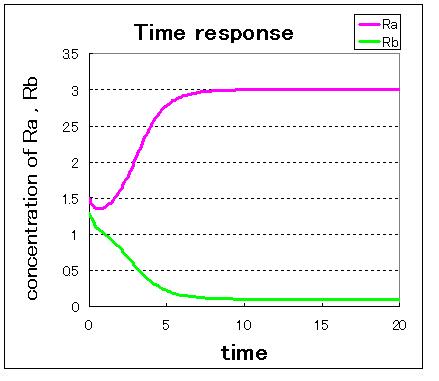
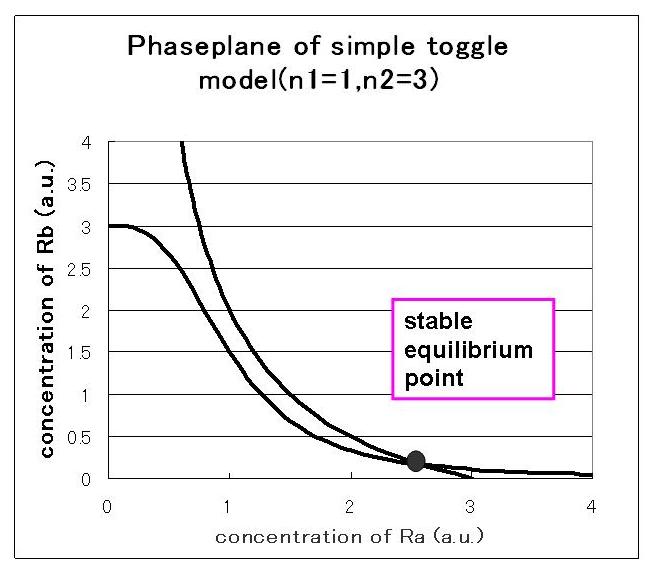
Next,when the number of stable equilibrium point is one, the result of simulation are shown in Fig●

Fig● indicate that when the initial condition is (Ra,Rb)=(0.0,2.5) and when the initial condition is (Ra,Rb)=(2.5,0.0), the values of Ra and Rb goes to stable equilibrium point B.

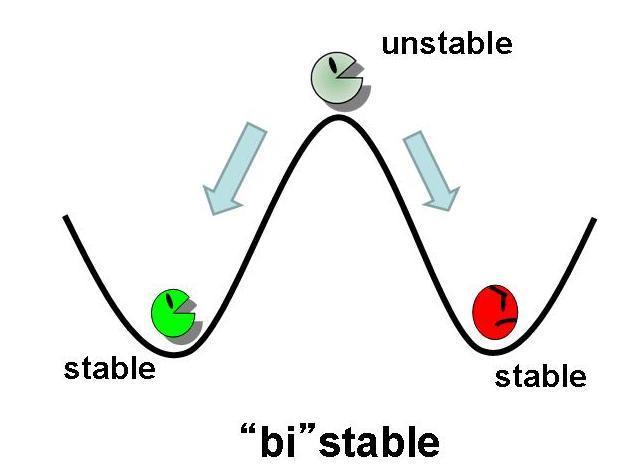
As a result,taking two stable status need the phaseplane of two stable equilibrium points and we have to set proper parameters.