Tokyo/Model

From 2007.igem.org

Balanced Redifferentiation of E.coli !

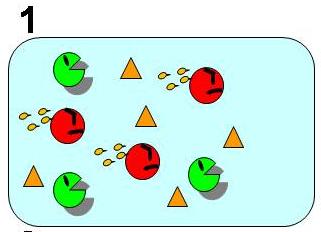
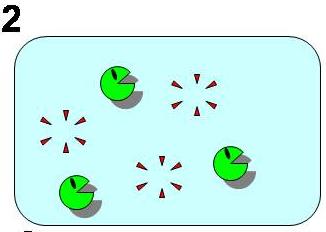
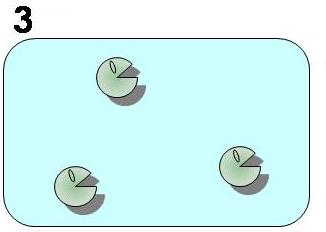
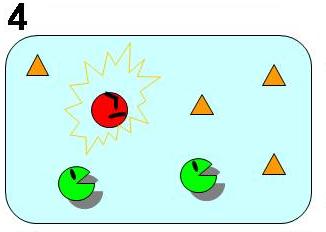
To follow Pareto’s principle found in an ant society, our model system must satisfy the three conditions shown in Fig. 1 to 4. In our model, all individual cells have the same genetic circuits but take either of stable state A (worker) or B (idler) depending on the surrounding circumstances as if they are DIFFERENTIATE. They also change their states as if they DEDIFFERENTIATE and REDIFFERENTIATE so that the ratio of the two cell states is well balanced. ([http://en.wikipedia.org/wiki/Pareto_principle What is Pareto's principle? (Wikipedia)])

As shown in Fig. 1, 2, 3, and 4, the condition of the system is changing as follows:

Bistable state ⇒ The removal of A (worker) ⇒ Dedifferentiation of B(idlers)⇒ Balanced Redifferentiation into A and of B

Fig. 1 Condition 1. Bistable state at balanced ratio of differentiated A and B
The system is stable when it contains both A (worker) and B (idler) "balanced" at certain ratio.

Fig. 2 Condition 2. Removal of A
Now that A (worker) is removed, there is only B (idler) left.

Fig. 3 Condition 3. Dedifferentiation of B
While after the removal of A (worker), B (idler) becomes unstable and dedifferentiates.

Fig. 4 Condition 4. Balanced Redifferentiation
Some Dedifferentiated cells redifferentiate into A (worker) while the others go back to B (idler). Then the system becomes stable again with the balanced ratio of A and B.