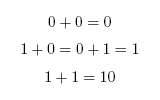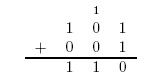Waterloo
From 2007.igem.org
 University of Waterloo iGEM Team
University of Waterloo iGEM Team Contents |
Our Team
The UW iGEM team is a very interdisciplinary group. Our team members span the three faculties of Science, Mathematics and Engineering and include the programs of Biology, Biomedical Sciences, Computer Science, Bioinformatics, Computer Engineering, Electrical Engineering, Chemical Engineering, and Mathematical Physics at undergraduate and graduate levels. Even our professor advisors are cross-appointed to two other faculties. Our diverse backgrounds bring together a wide range of skills and ideas to the iGEM project. iGEM is giving us the opportunity to apply the skills learned in our lectures and labs to real life applications in molecular biology and biotechnology.
Abstract
Background
Binary Addition
When working in binary, only two digits are used: 0 and 1. Counting therefore proceeds as:
- 1
- 10
- 11
- 100
- 101
- 111
etc.
To add two binary numbers, the process is much the same as adding two decimal (ordinary) numbers, except that instead of carrying when two digits add to ten, carrying must be performed when two digits add to two. In other words, 0 + 1 adds to 1, but 1 + 1 adds to 0 with a carry of 1, which gives 10 (just as in decimal 1 + 9 would add to 0 with a carry of 1, to give 10). A complete list of the possibilities is as follows:
Half-Adder vs Full-Adder
Any construct designed to add two numbers will either be a half-adder or a full-adder. A half-adder can only add together two single digits, whereas a full-adder is needed to add two numbers of any length greater than one digit.
For example, a half-adder could perform the addition 1 + 0 = 1, or 1 + 1 = 10, but it would take a full-adder to be able to perform 1100101 + 100101.
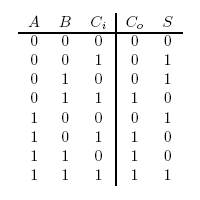
In terms of implementation, a half-adder accepts two inputs (the two digits to be summed) and returns two outputs (the "sum bit" and the "carry bit"). To add 1 + 1, the two inputs would each be 1, the sum bit would be 0, and the carry bit would be 1. A full list of the possibilities is shown in Figure 1.
A full-adder is merely a half-adder that accepts an extra input; namely, the carry bit from another full-adder. Each full-adder is responsible for adding one pair of corresponding digits from the two numbers to be added, and it must add to that the carry bit from the previous full-adder. The full-adder will output the resulting sum bit and carry bit, and the process will continue until all the digits have been added. Such a chain of full-adders is called a ripple carry adder. See Figure 2 for a full list of possibilities.
[[Image:111.jpg] "Half-Adder Truth Table"]
Figure 2: Full Adder Truth Table
Figure 3: Long Addition of 101 + 001
Logic Gates and Implementing an Adder
A logic gate is a device that accepts two binary input(s) (each a 0 or 1) and returns one binary output. A list of relevant logic gates is as follows:
- OR gate
- XOR gate
- AND gate
- NOT gate
For the following explanations, A and B represent statements that can be either true or false.
OR Gate
Consider the statement "A OR B". If either A or B is true, the statement is said to be true. The only time this statement will be false is if both A and B are false. This is the meaning of the OR operation.
An OR gate accepts two binary inputs, where a 1 to represents "true" and a 0 represents "false". The output of the OR gate is also binary, and similarly represents either "true" or "false".
To illustrate,
0 OR 0 = 0 1 OR 0 = 0 OR 1 = 1 1 OR 1 = 1
XOR Gate
XOR is an abbreviation for "exclusive OR". The XOR gate is similar to the OR gate, the only difference being that it will return false if both inputs are true.
For example,
1 XOR 0 = 1 1 XOR 1 = 0
AND gate
The AND gate will return 1 (true) only if both the inputs are 1 (true). Otherwise, it will return a 0.
To illustrate,
0 AND 0 = 0 1 AND 0 = 0 AND 1 = 0 1 AND 1 = 1
NOT gate
The NOT gate accepts one input, and simply switches its value.
NOT 1 = 0 NOT 0 = 1
Using logic gates to make an adder
Given two binary inputs A and B, their sum can be computed by passing these inputs through various logic gates. The process is illustrated in Figures 4 and 5.
DNA as Logic Gates
The crux of our project is the idea of using DNA as logic gates.
Project Details
Inputs (stimuli and the genes used to detect them)
Output (observable change and what it represents)
Gene Diagram
Testing/Results
Mathematical Model
Measurements
Extensions
Full Adder
==Acknowledgements== (Sponsor logos)