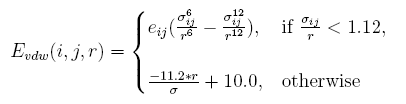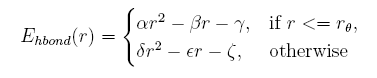From 2007.igem.org

Introduction

Protein Design

Designing efficient proteins for a broad of different processes is of tremendous practical fun both in science and industry. [1]. Computational design is well concerned for its efficiency and convenience. Redesigning the protein-DNA complexes is so important that it is the first step concerned at the beginning of redesigning the active sites. Some milestones have been reported[2-5]. Here we are trying to construct several artificial repressor-operator pairs to serve as the connecting wires of our system.

There are several steps in protein design[6]. Firstly, generate a random structure with random sequence. Secondly, optimize the structure of the side-chains for each random sequence. Thirdly, give each random sequence a score and select the sequence with the best score. In almost all the conditions, sequence candidates is countless. There will be 20²⁰ candidates if we redesign 20 positions. Therefore, great efforts have been made to reduce the computation complexity[1,7-14], for example, using rotamer representing several discrete conformation, to work out the status of sidechains, employing pair-wise energy function to score the sequence, searching with Monte Carlo, Genetic Algorithm and etc. Another key here is the score function. Up till now, no efficient method in silico has been given to examine the computational design results. One way to examine them is to express the sequences designed in practical experiments.

Lac Repressor

Figure 1 Solution structure of a dimer of Lac repressor DNA-binding domain complexed to its natrual operator O1 ([http://www.rcsb.org/pdb/explore.do?structureId=1L1M From RCSB])

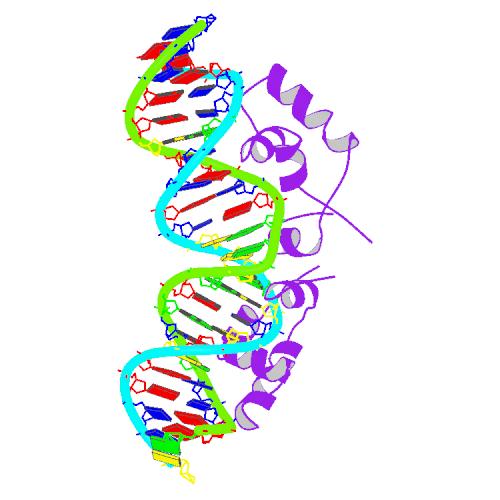
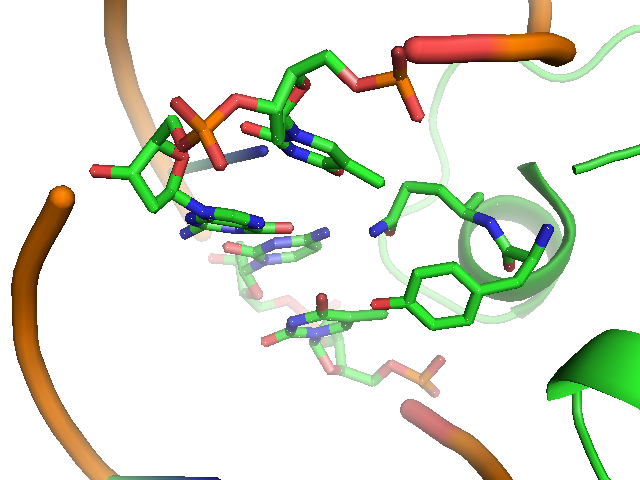
The lac repressor is a DNA-binding protein which inhibits the expression of genes coding for proteins involved in the metabolism of lactose in bacteria[15]. There are three distinct regions in the protein. The headpiece ,which is a fragment with about 51 amino acids from its N-terminal and consists a helix-turn-helix motif , is the only region working for binding DNA. Figure 1 shows the NMR structure of the complex with two headpieces of lac repressor and its nature operator[16]. A series of experiments have shown that the mutation on the 7th, 9th site on the operator can sharply decrease the stability of the complex[15-17]. Figure 2 shows the structure of DNA sequence on site 7,8,9 and the residues interaction with them. From the structure, we can get that residue 17,18, which are YQ in native repressor sequence, take charge in recognizing the specific DNA sequence. The binding specificity may be adapted by changing the two positions.

For wires without interference, the binding specificity is highly requirement for the repressor-operator pairs. It is reported that the mutated repressor with VA on the position 17,18 can bind with the transition mutated operator on the site 7 [18]. Tranversion can lead to too great change that the DNA structure can not be built according to native structure and no mutated lac repressors can bind it. So only transition mutation done on the DNA, and the structure was built manually according to native structure, then optimized with gromos96, 43a1 forcefield. In this way, we obtain four DNA structures, and our aim is to redesign the recognize parts on the repressor to make it bind the DNA specific.

Figure 2 The structure of DNA sequence on site 7,8,9 of the recognition helix of Lac repressor and the residues interaction with them

Computational Model

Score function

Our score function here is a combination of physic-based potentials and knowledge-based potentials. The energy items should be modified to suitable with rotamer library. The modified van der waal interaction, hydrogen bond energy, solvent accessible surface area (SASA) and electrostatic interaction are employed as items for score function.

Linearize van der waal interaction

The vdw interaction energy[19] between atom i and atom j at the distance of r is:

Clashes will be more than native structure, caused by discrete represent proteins sidechains. A tolerate acception of clash is given by linearizing the resplusize item in the vdw energy, and the parameter are decided by test.

Hydrogen bond energy

given the distance between the donor and acceptor, the hydrogen bond energy is:

Describing sidechain structure with rotamers is changing the distance between the donor and acceptor too, and the position of hydrogen atom can not be obtained in a easy way as it rotates. Here we build a knowledge-base potential base d on the distance of donor and acceptor in the coarse-grained structures.

SASA and Electrostatic Interaction

The energy items for SASA and electostatic interaction are defined by TM Handel and her co-workers[8].

Sampling

We optimize sidechain of the proteins and select sequence with different score function. Because they are totally different processes on concept. Sidechain optimization tells us the 3-dimensional structure of the complex after changing the amino acids in the protein and the amino acid sequence selection tells us which sequence is more suitable for binding. The role of each energy item is not the same in two process . The parameters for sidechain optimized are obtained by training with 49 structures picked from PDBbind library [20], and they for sequence selection are by training with the results of directed evolution.

Results

In this particular problem, only 2 positions on the protein to be changed, so there are only 400 candidates. The computational complexity is no more a problem here. We optimized the sidechain of each candidate, and get the each energy items. With the directed evolution, we find the suitable parameters for sequence selection and predict that some other chains may work in this problem. And the experiments of test are processing.

References

1. Zanghellini, A.; Jiang, L.; Wollacott, A. M.; Cheng, G.; Meiler, J.; Althoff, E. A.; Röthlisberger, D. & Baker, D. (2006), 'New algorithms and an in silico benchmark for computational enzyme design.', Protein Sci 15(12), 2785--2794.
2. Dahiyat, B. I. & Mayo, S. L. (1997), 'De novo protein design: fully automated sequence selection.', Science 278(5335), 82--87.
3. Kuhlman, B.; Dantas, G.; Ireton, G. C.; Varani, G.; Stoddard, B. L. & Baker, D. (2003), 'Design of a novel globular protein fold with atomic-level accuracy.', Science 302(5649), 1364--1368.
4. Looger, L. L.; Dwyer, M. A.; Smith, J. J. & Hellinga, H. W. (2003), 'Computational design of receptor and sensor proteins with novel functions.', Nature 423(6936), 185--190.
5. Ashworth, J.; Havranek, J. J.; Duarte, C. M.; Sussman, D.; Monnat, R. J.; Stoddard, B. L. & Baker, D. (2006), 'Computational redesign of endonuclease DNA binding and cleavage specificity.', Nature 441(7093), 656--659.
6. Lippow, S. M. & Tidor, B. (2007), 'Progress in computational protein design.', Curr Opin Biotechnol 18(4), 305--311.
7. Georgiev, I.; Lilien, R. H. & Donald, B. R. (2006), 'Improved Pruning algorithms and Divide-and-Conquer strategies for Dead-End Elimination, with application to protein design', Bioinformatics 22, e174-83.
8. Pokala, N. & Handel, T. M. (2004), 'Energy functions for protein design I: efficient and accurate continuum electrostatics and solvation.', Protein Sci 13(4), 925--936.
9. Gordon, D. B.; Hom, G. K.; Mayo, S. L. & Pierce, N. A. (2003), 'Exact rotamer optimization for protein design', Journal of Computational Chemistry 24, 232-43.
10. Holm, L. & Sander, C. (1992), 'Fast and simple Monte Carlo algorithm for side chain optimization in proteins: application to model building by homology', Proteins 14, 213-23.
11. Lilien, R. H.; Stevens, B. W.; Anderson, A. C. & Donald, B. R. (2005), 'A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase a phenylalanine adenylation enzyme.', J Comput Biol 12(6), 740--761.
12. Pokala, N. & Handel, T. M. (2005), 'Energy functions for protein design: adjustment with protein-protein complex affinities, models for the unfolded state, and negative design of solubility and specificity.', J Mol Biol 347(1), 203--227.
13. Shah, P. S.; Hom, G. K. & Mayo, S. L. (2004), 'Preprocessing of rotamers for protein design calculations', Journal of Computational Chemistry 25, 1797-800.
14. Street, A. G. & Mayo, S. L. (1998), 'Pairwise calculation of protein solvent-accessible surface areas.', Fold Des 3(4), 253--258.
15. Lewis, M.; Chang, G.; Horton, N. C.; Kercher, M. A.; Pace, H. C.; Schumacher, M. A.; Brennan, R. G. & Lu, P. (1996), 'Crystal structure of the lactose operon repressor and its complexes with DNA and inducer.', Science 271(5253), 1247--1254.
16. Lehming, N.; Sartorius, J.; Niemöller, M.; Genenger, G.; v Wilcken-Bergmann, B. & Müller-Hill, B. (1987), 'The interaction of the recognition helix of lac repressor with lac operator.', EMBO J 6(10), 3145--3153.
17. Sartorius, J.; Lehming, N.; Kisters, B.; von Wilcken-Bergmann, B. & Müller-Hill, B. (1989), 'lac repressor mutants with double or triple exchanges in the recognition helix bind specifically to lac operator variants with multiple exchanges.', EMBO J 8(4), 1265--1270.
18. Salinas, R. K.; Folkers, G. E.; Bonvin, A. M. J. J.; Das, D.; Boelens, R. & Kaptein, R. (2005), 'Altered specificity in DNA binding by the lac repressor: a mutant lac headpiece that mimics the gal repressor.', Chembiochem 6(9), 1628--1637.
19. Grigoryan, G.; Ochoa, A. & Keating, A. E. (2007), 'Computing van der Waals energies in the context of the rotamer approximation.', Proteins 68(4), 863--878.
20. Wang, R.; Fang, X.; Lu, Y. & Wang, S. (2004), 'The PDBbind database: collection of binding affinities for protein-ligand complexes with known three-dimensional structures.', J Med Chem 47(12), 2977--2980.