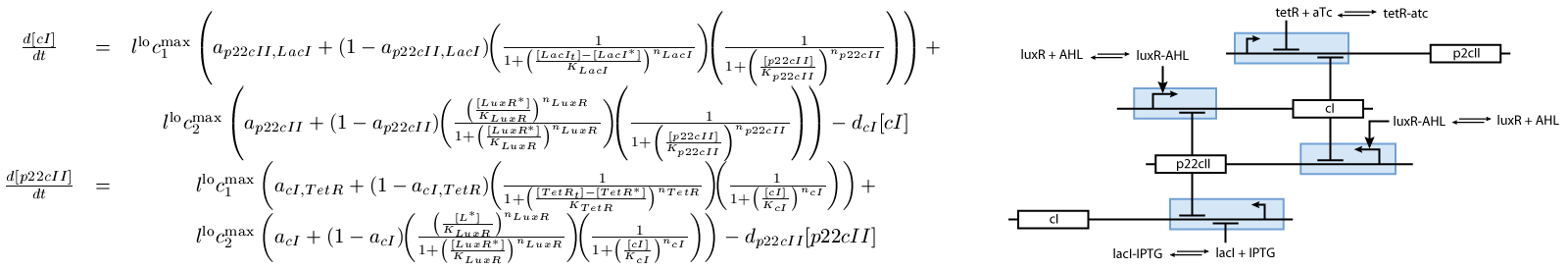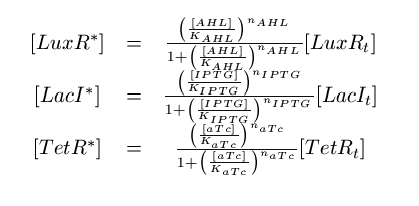ETHZ/Engineering

From 2007.igem.org

< ETHZ

Revision as of 19:18, 7 October 2007 by Cbergeles (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Main Page Biology Pespective Engineering Perspective Meet the Team Team Notes Pictures!

.:: EducatETH E. coli - Engineering Perspective ::.

.:: Introduction ::.

In order to understand if it is possible to create the learning system that we wanted, we had to run some initial simulations, to see if we could reach the desirable steady states. After creating a basic framework on which to work on, we refined the parameters by searching the available literatures. In the next, we are presented the coupled differential equations that model our system, their parameters and the values that we picked, the results of our simulations, and lastly, we provide our references. For an introduction to system modeling in synthetic biology, please read our modeling tutorial here.

.:: System Model ::.

Following the guidelines presented in our modeling guide, we divided the biological system into subsystems, each of which was modelled with a system of differential equations. According to what presented in the Biology Perspective, our system is composed the following three subsystems:

A subsystem of constitutively produced proteins (see Fig. 1),
The learning part (see Fig. 2), and
The reporting subsystem (see Fig. 3).

The first two subsystems interact, and thus, they should be considered together. The third subsystem has no feedback with the other two, as it is only used for producing the appropriate fluorescent proteins. The subsystem with the constitutively produced proteins serves as a regulatory system, and can be modeled with three decoupled partial differential equations (see Fig. 1):

Subsystem 1: Constitutively produced proteins (Fig. 1)

The second subsystem is the main part of the biological model. This subsystem stores the information concerned the learned chemical, and drives the production of the appropriate reporter, during the recognition phase. It is actually a toggle switch, that reaches a steady state depending on the chemical that it is exposed to (see Fig. 2):

Subsystem 2: Basic learning subsystem (toggle) (Fig. 2)

The third subsystem reports the state that our system is, during the different phases of learning and recognition. During the learning phase, this subsystem reports which chemical the cells are exposed to, and during the recognition phase, it reports if the cells recognize the chemicals that they are currently exposed to (see Fig. 3):

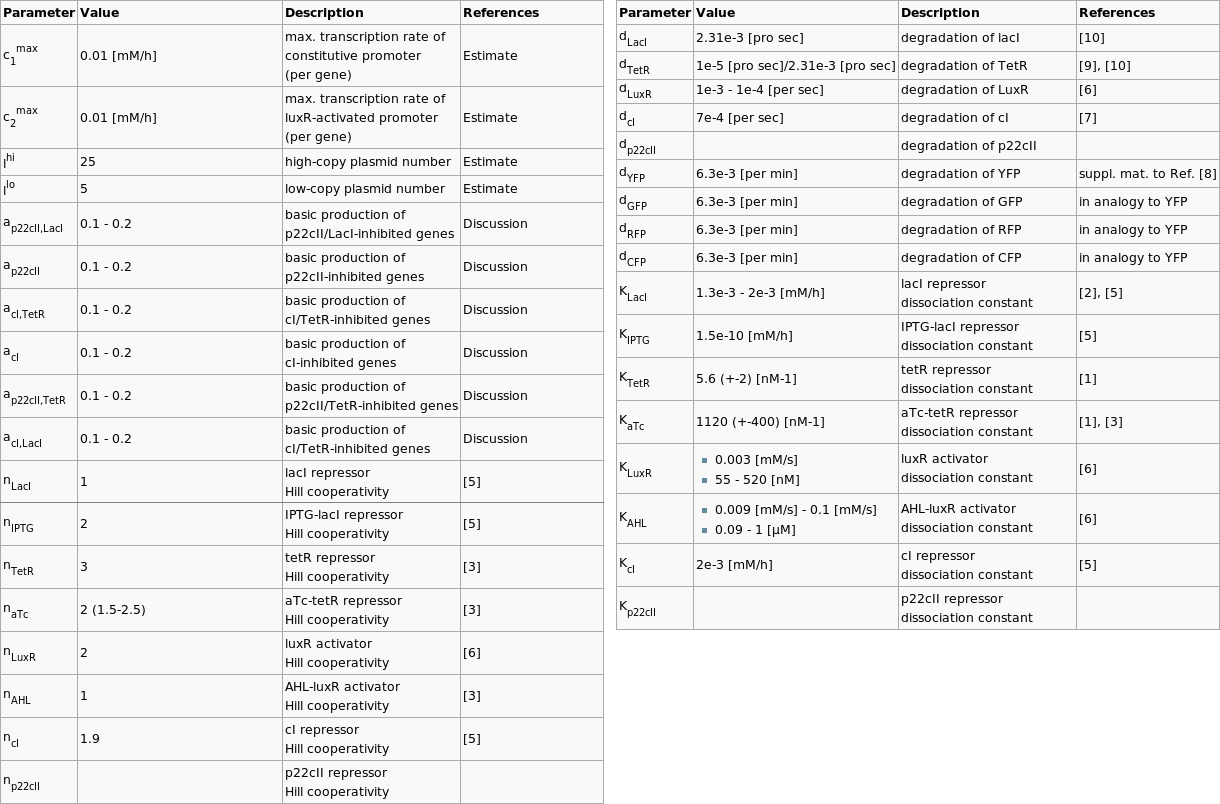
Subsystem 3: Reporting subsystem (Fig. 3)

Note that the three constitutively produced proteins LacI, TetR and LuxR exist in two different forms; as free proteins and in complexes they build with IPTG, aTc and AHL, respectively. We need to model this complex-forming procedure, with another set of differential equations (Fig. 4):

Allosteric regulation (see Fig. 4)

In order to have meaningful results from our simulations, we browsed through the literature in order to find appropriate values for our parameters. We reduced our parameter space by joining parameters together, and we gave reasonable estimates, for the values that could not be extracted from available publications. Since this is a hard part that every team has to face, we present the table with the chosen parameters below:

Parameters of the model (Fig. 5)

Parameter	Value	Description	References
c₁^max	0.01 [mM/h]	max. transcription rate of constitutive promoter (per gene)	Estimate
c₂^max	0.01 [mM/h]	max. transcription rate of luxR-activated promoter (per gene)	Estimate
l^hi	25	high-copy plasmid number	Estimate
l^lo	5	low-copy plasmid number	Estimate
a_p22cII,LacI	0.1 - 0.2	basic production of p22cII/LacI-inhibited genes	Discussion
a_p22cII	0.1 - 0.2	basic production of p22cII-inhibited genes	Discussion
a_cI,TetR	0.1 - 0.2	basic production of cI/TetR-inhibited genes	Discussion
a_cI	0.1 - 0.2	basic production of cI-inhibited genes	Discussion
a_p22cII,TetR	0.1 - 0.2	basic production of p22cII/TetR-inhibited genes	Discussion
a_cI,LacI	0.1 - 0.2	basic production of cI/TetR-inhibited genes	Discussion
d_LacI	2.31e-3 [pro sec]	degradation of lacI	[10]
d_TetR	1e-5 [pro sec]/2.31e-3 [pro sec]	degradation of TetR	[9], [10]
d_LuxR	1e-3 - 1e-4 [per sec]	degradation of LuxR	[6]
d_cI	7e-4 [per sec]	degradation of cI	[7]
d_p22cII		degradation of p22cII
d_YFP	6.3e-3 [per min]	degradation of YFP	suppl. mat. to Ref. [8]
d_GFP	6.3e-3 [per min]	degradation of GFP	in analogy to YFP
d_RFP	6.3e-3 [per min]	degradation of RFP	in analogy to YFP
d_CFP	6.3e-3 [per min]	degradation of CFP	in analogy to YFP
K_LacI	1.3e-3 - 2e-3 [mM/h]	lacI repressor dissociation constant	[2], [5]
K_IPTG	1.5e-10 [mM/h]	IPTG-lacI repressor dissociation constant	[5]
K_TetR	5.6 (+-2) [nM-1]	tetR repressor dissociation constant	[1]
K_aTc	1120 (+-400) [nM-1]	aTc-tetR repressor dissociation constant	[1], [3]
K_LuxR	0.003 [mM/s] 55 - 520 [nM]	luxR activator dissociation constant	[6]
K_AHL	0.009 [mM/s] - 0.1 [mM/s] 0.09 - 1 [µM]	AHL-luxR activator dissociation constant	[6]
K_cI	2e-3 [mM/h]	cI repressor dissociation constant	[5]
K_p22cII		p22cII repressor dissociation constant
n_LacI	1	lacI repressor Hill cooperativity	[5]
n_IPTG	2	IPTG-lacI repressor Hill cooperativity	[5]
n_TetR	3	tetR repressor Hill cooperativity	[3]
n_aTc	2 (1.5-2.5)	aTc-tetR repressor Hill cooperativity	[3]
n_LuxR	2	luxR activator Hill cooperativity	[6]
n_AHL	1	AHL-luxR activator Hill cooperativity	[3]
n_cI	1.9	cI repressor Hill cooperativity	[5]
n_p22cII		p22cII repressor Hill cooperativity

.:: Simulations ::.

.:: References ::.

[1] Weber W., Stelling J., Rimann M., Keller B., Daoud-El Baba M., Weber C.C., Aubel D., and Fussenegger M., "A synthetic time-delay circuit in mammalian cells and mice", Proceedings of the National Academy of Sciences, vol. 104, no. 8, pp. 2643, 2007.
[2] Setty Y., Mayo AE, Surette MG, and Alon U., "Detailed map of a cis-regulatory input function", Proceeding of the National Academy of Sciences, vol. 100, no. 13, pp. 7702--7707, 2003.
[3] Braun D., Basu S., and Weiss R., "Parameter Estimation for Two Synthetic Gene Networks: A Case Study", IEEE Int'l Conf. Acoustics, Speech, and Signal Processing 2005, vol. 5, 2005.
[4] Fung E., Wong W.W., Suen J.K., Bulter T., Lee S., and Liao J.C., "A synthetic gene--metabolic oscillator", Nature, vol. 435, no. 7038, pp. 118--122, 2005, supplementary material.
[5] Iadevaia S., and Mantzaris N.V., "Genetic network driven control of PHBV copolymer composition", Journal of Biotechnology, vol. 122, no. 1, pp. 99--121, 2006.
[6] Goryachev AB, Toh DJ, and Lee T., "Systems analysis of a quorum sensing network: Design constraints imposed by the functional requirements, network topology and kinetic constants", Biosystems, vol. 83, no. 2-3, pp. 178--187, 2006.
[7] Arkin A., Ross J., and McAdams H.H., "Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-Infected Escherichia coli cells", Genetics, vol. 149, no. 4, pp. 1633--1648, 1998.
[8] Colman-Lerner A., Chin T.E., and Brent R., "Yeast Cbk1 and Mob2 Activate Daughter-Specific Genetic Programs to Induce Asymmetric Cell Fates", Cell, vol. 107, no. 6, pp. 739--750, 2001.
[9] Becskei A., and Serrano L., "Engineering stability in gene networks by autoregulation", Nature, vol. 405, no.6786, pp.590--593, 2000.
[10] Tuttle L.M., Salis H., Tomshine J., and Kaznessis Y.N., "Model-Driven Designs of an Oscillating Gene Network", Biophysical Journal, vol. 89, no. 6, pp. 3873--3883, 2005.

.:: To Do ::.

'Christos': 1. Add gifs concerning the simulations

Views