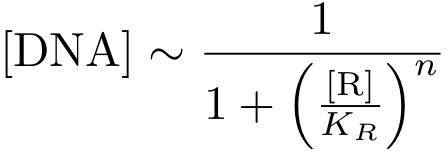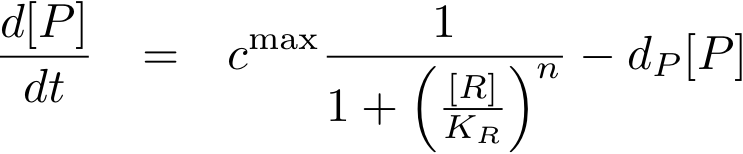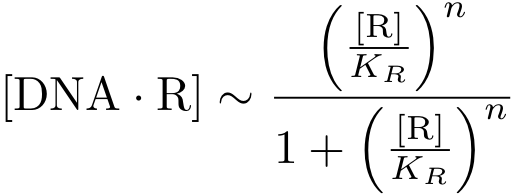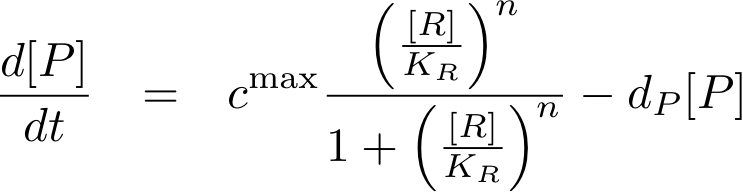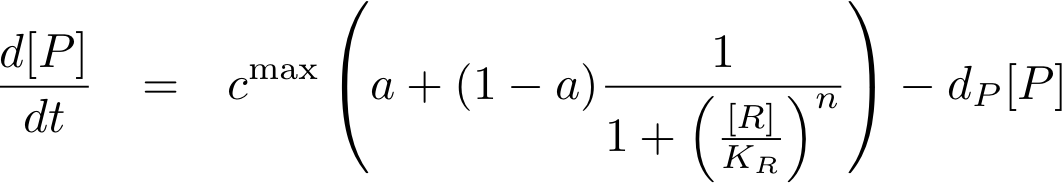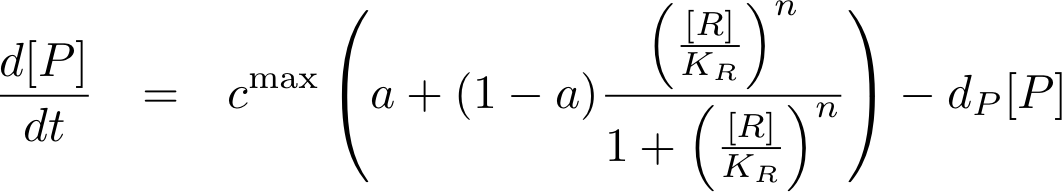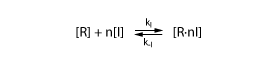From 2007.igem.org

Main Page      System Modeling      Simulations      System Implementation      Lab Notes      Meet the Team      Team Notes      Pictures!

Modeling Basics

The functioning of our model depends mostly on protein concentrations. These proteins are produced within the E. coli cells, based on genes that we introduced into the cell. To understand the system, it is crucial to model the gene expression and regulation accurately.

This Wiki page is intended to present the basic mechanisms and assumptions that went into the mathematical description of our iGEM model.

Constitutive Protein Production

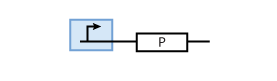
The most simple parts in the system are genes that are continuously transcribed to produce a protein. At the same time, proteins have a certain half-life time, which means that they are degraded. This leads to the following simple model of protein production/degradation shown in Fig. 1.

To find the concentration of protein P (as a function of time), the system of Fig. 1 can be written as ordinary differential equation (ODE)

This equation states that the change of protein concentration is a function of protein production (c^max) and protein degradation (d_P[P]).

It is worth looking at the protein production a bit closer. The production of protein P depends on the expression of a gene that codes for this protein. In the case of constant protein production, the gene can be modeled by a constitutive promoter and a coding region for the protein (Fig. 2).

Regulated Protein Production

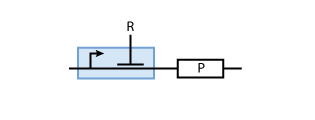
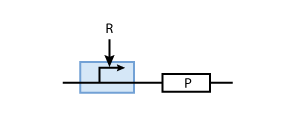
To build a system with logic functionality, it is necessary to produce a protein depending on the concentration of another protein (i.e. a transcription factor). To model such a system, the promoter of the constitutive production system in Fig. 2 must be extended to take into account the presence of the regulatory protein R. There are two possible cases: the regulatory protein either inhibits or activates the expression of the gene (see Figs. 3 and 4, respectively).

Inhibition

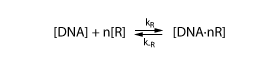
To derive the equations describing the regulated transcription, we first need a model how the transcription factor interacts with DNA. The most simple model is when the protein binds reversibly to the DNA:

Note that the equation above involves n transcription factors. For certain transcription factors the number of proteins involved is indeed greater than 1. These are interesting cases that enable applications such as toggle switches.

When the transcription factor binds to DNA, it blocks the enzymes transcribing the gene. Thus, the higher the concentration of R, the smaller the transcription of the gene. By controlling the concentration of the regulatory protein R, the expression of protein P can effectively be regulated.

To understand this process in more detail, we make the simplification that the binding of R to DNA is in equilibrium. That is, one can write

In case of inhibition, the expression of the gene is proportional to the probability that the DNA is 'free' (meaning that there is no transcription factor bound to it). After some algebraic manipulation of the above equation an expression for the 'free DNA' as a function of transcription factor concentration can be derived:

Now, we have basically everything together to write down a differential equation for the concentration of protein P whose expression is regulated by protein R:

The transcription does not always take place at the maximum rate c^max as was the case for the constitutively produced proteins, but is modulated by the concentration of protein R.

Activation

To understand activation, we start from the same model of the transcription factor binding reversibly to DNA

But in case of activation, we are interested in the DNA - transcription factor complex, because the transcription rate is proportional to the probability that a protein is bound to DNA.

Assuming equilibrium conditions as in the inhibition case, we can derive an expression for the DNA-protein complex concentration as a function of protein concentration:

Analogously, we can now write the whole differential equation for protein concentration if transcription is activated by protein R

Basic Production

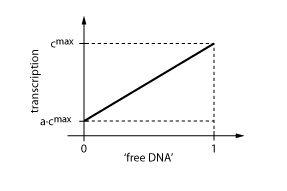
The equations so far assume perfect inhibition/activation. This means, in case of inhibition, that if the inhibitor concentration is high enough, the transcription of protein P is practically zero. Or, in the case of activation, that in the absence of activator protein there is no transcription. In reality, one observes always some basic production, despite high inhibitor concentrations or absence of activator protein. The basic transcription is usually around 10-20% of the maximum transcription rate. The case of inhibition is illustrated in Fig. 5.

Thus we have to introduce some 'basic transcription' that always takes place. For inhibition we have

and for activation

Note that the basic transcription rate is introduced as a leakiness factor a, which is a percentage of the maximum transcription rate c^max. Regulation of transcription by protein R now is only effective in the range between a·c^max and c^max.

Inducer Molecules

A problem in biology is that regulatory proteins (such as protein R in the previous sections) cannot be used as system inputs directly. It is not possible to add such proteins to an assay to steer the behavior of a biological system, because these proteins are big and do not diffuse through cell walls. They cannot enter the cell.

To circumvent this limitation, one has to produce these proteins directly in the cell. But then, one needs a possibility to switch the functionality of these proteins on and off. This is where inducer molecules become useful. Inducer molecules are small molecules that can diffuse through cell walls freely. Furthermore, they are able to bind to the regulatory proteins and switch the functionality on or off.

Thus, we need a model to describe the binding of the inducer to the protein. We assume again that the inducer I binds reversibly to the protein R

We assume once more that this reaction is in equilibrium. We thus have

Depending on the species at hand we are either interested in the protein-inducer complex concentration of in the concentration of 'free protein'. For some species (e.g. luxR), the complex form is functional and for others it is the free protein (e.g. tetR).