Tokyo/Formulation/5.stochastic differential equation model with poisson random variables

From 2007.igem.org

< Tokyo/Formulation
Revision as of 15:35, 24 October 2007 by Akama (Talk | contribs)

we introduced the terms of Ex 4-1 into a stochastic process to simulate the sthochastic behavior.we used Poisson random variables as a sthochastic process. Threfore,a stochastic differential equations were given as


Ex 5-1
Table 5


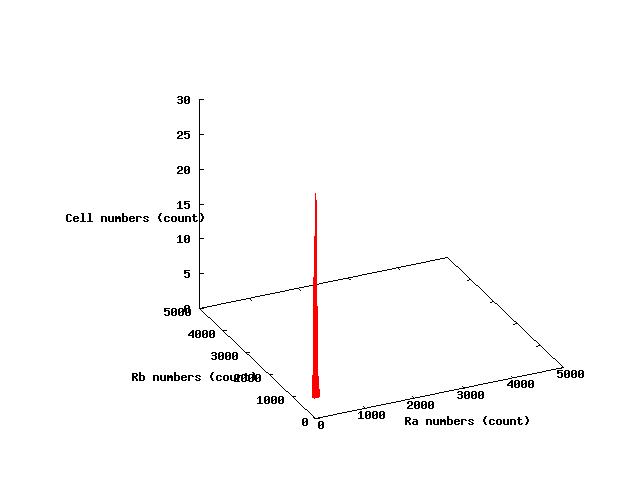
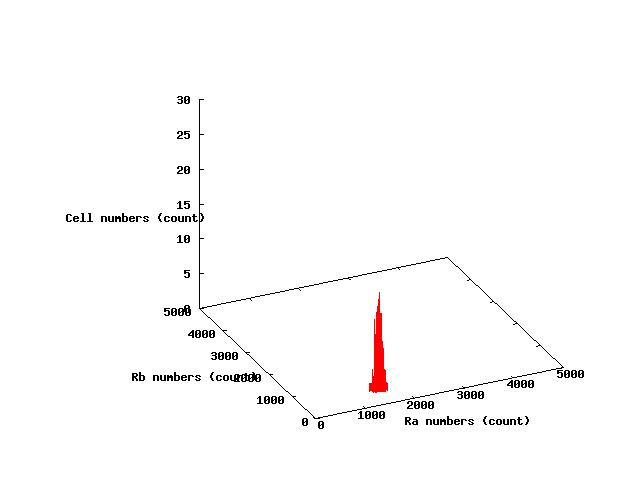
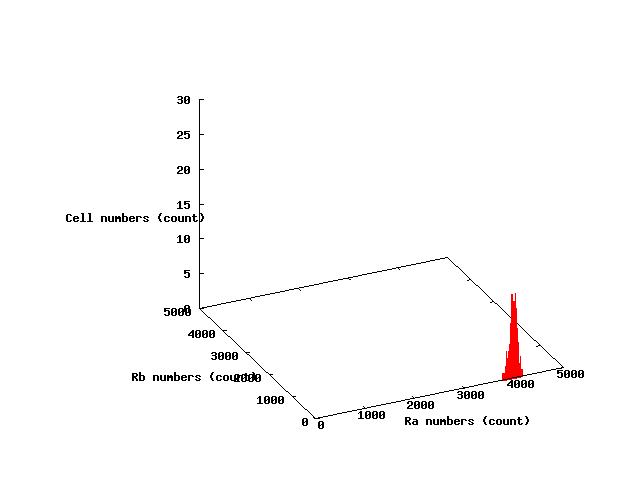
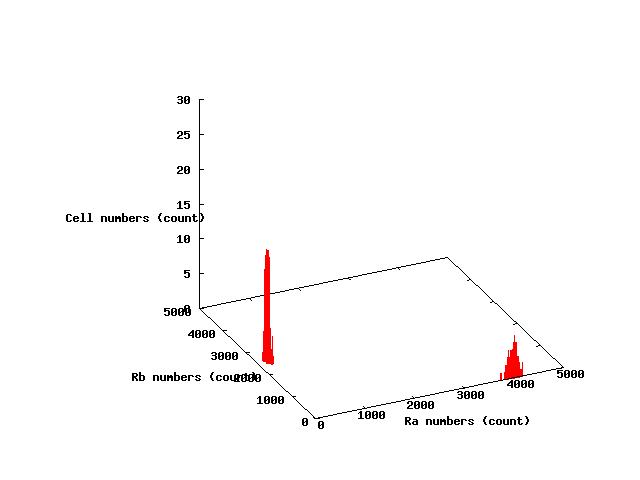
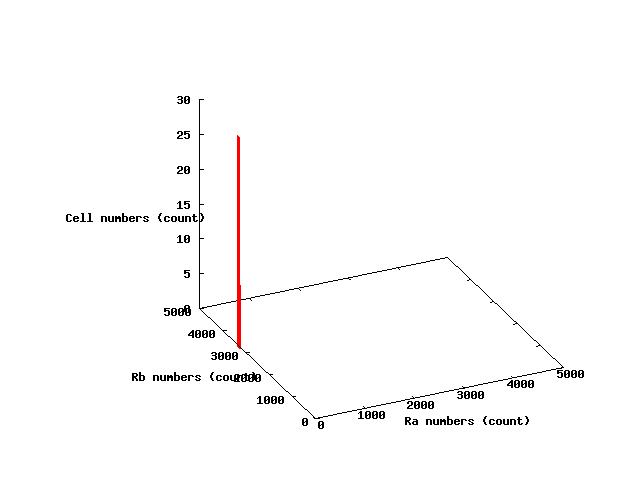
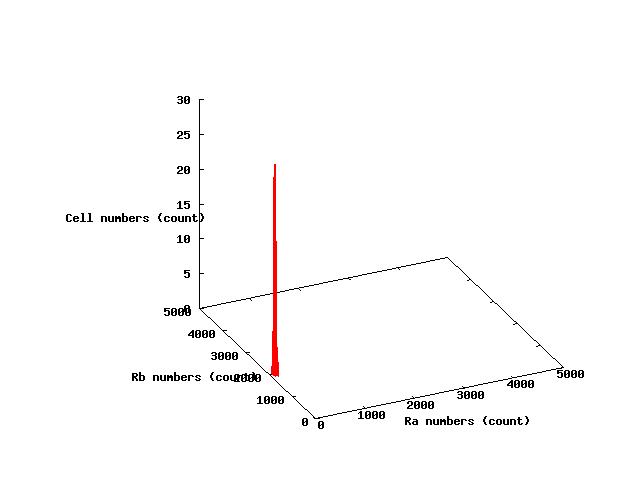
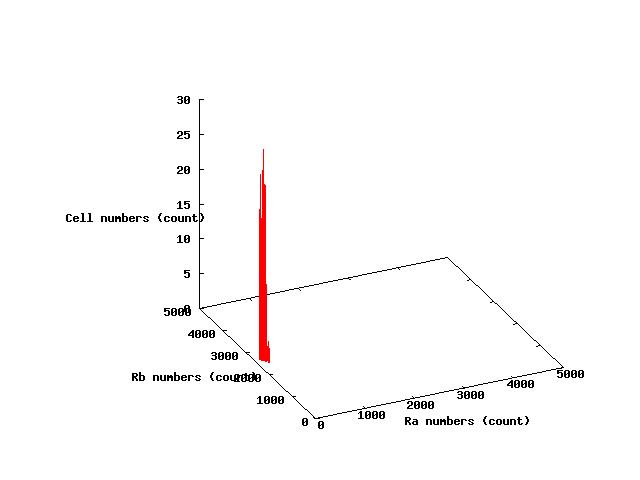
The values of parameters in the right table were used and the results of simulation were shown in Fig 5.1-3.
where α2 = 1(μM) in Fig 5.1,α2 = 2.7(μM) in Fig 5.2,α2 = 4(μM) in Fig 5.3. and it has been estimated that 1(μM) = 1000 molecules (count).

Figure 5.1.A 　t=0.2(min)
Arrow2.JPG
Figure 5.1.B 　t=0.8(min)
Arrow2.JPG
Figure 5.1.C 　 t=30(min)　only A

movie here!!


Figure 5.2.A 　t=0.2(min)
Arrow2.JPG
Figure 5.2.B 　 t=0.8(min)
Arrow2.JPG
Figure 5.2.C 　 t=30(min)　　success!! coexistence

movie here!!


Figure 5.3.A 　 t=0.2(min)
Arrow2.JPG
Figure 5.3.B 　 t=0.8(min)
Arrow2.JPG
Figure 5.3.C 　 t=30(min)　　 only B

movie here!!



Fig.5.1 indicates that all cells shift to A state in the steady state and Fig 5.3 indicates that all cells shift to B state in the steady state.These results doesn't represent coexistence stable.
Fig.5.2 indicates that a portion of cells shift to A state and the others shift to B state in steady state;that is,individual cells are stable under stable coexistence.


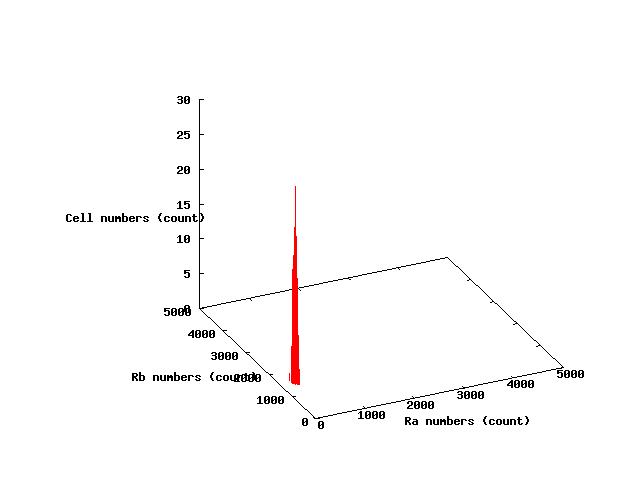
Next，the relation between the results of simulation and phase plane are shown in Fig.5.4.where nullclines is used Simulationの結果と相平面の関係を見てみる．相平面のヌルクラインはEx4-3を用いている．

Figure 5.4.1
Figure 5.4.2
Figure 5.4.3


これたの図から相平面上の安定点と大腸菌の分布とが一致しているの分かる．

Retrieved from "http://2007.igem.org/wiki/index.php/Tokyo/Formulation/5.stochastic_differential_equation_model_with_poisson_random_variables"