Tokyo/Formulation/5.stochastic differential equation model with poisson random variables

From 2007.igem.org

< Tokyo/Formulation
Revision as of 21:22, 24 October 2007 by Kiga (Talk | contribs)

we introduced the terms of Ex 4-1 into a stochastic process to simulate the sthochastic behavior.we used Poisson random variables as a sthochastic process. Threfore,a stochastic differential equations were given as


Ex 5-1
Table 5


ここより下は独立したページにすべき？



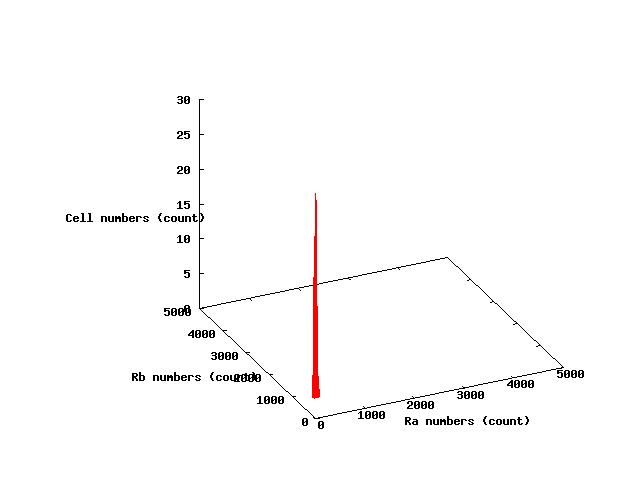
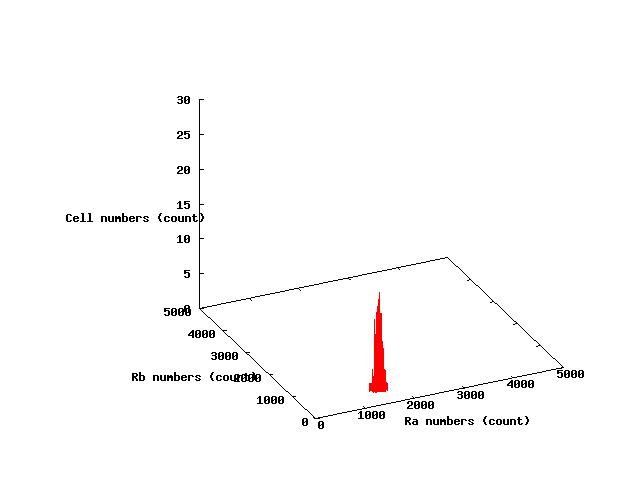
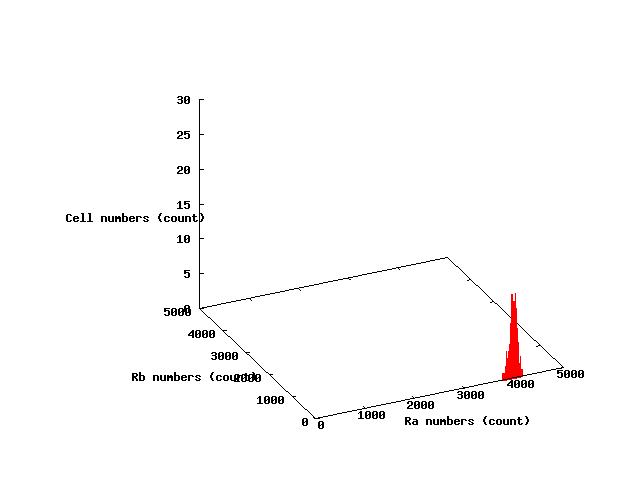
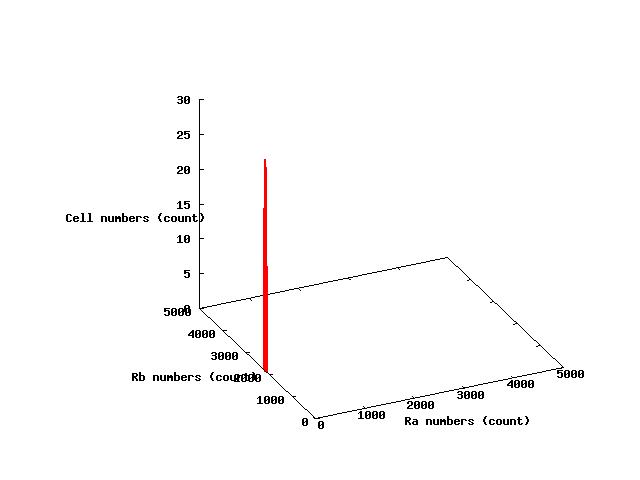
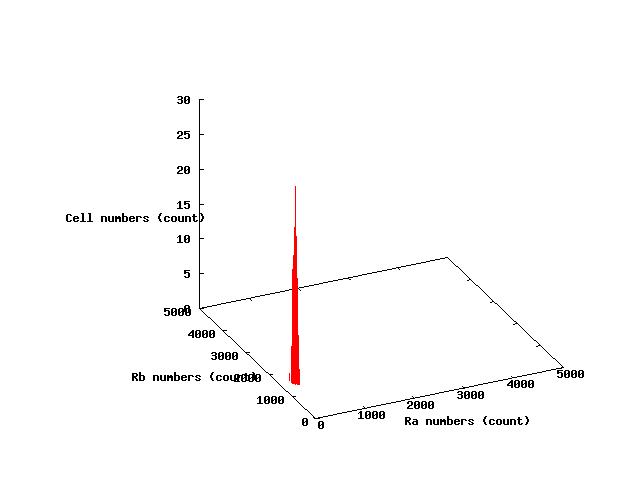
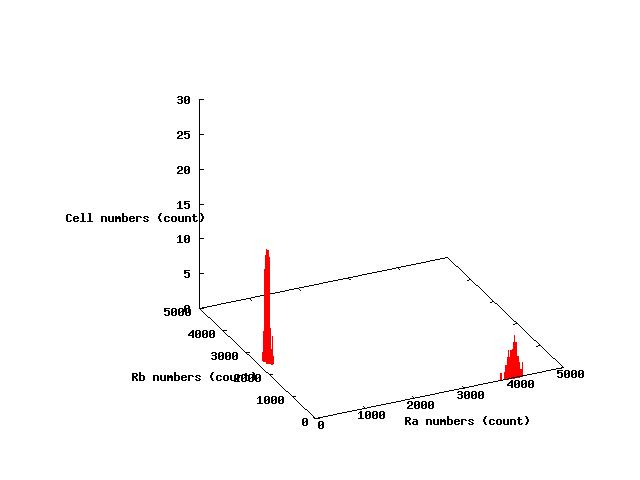
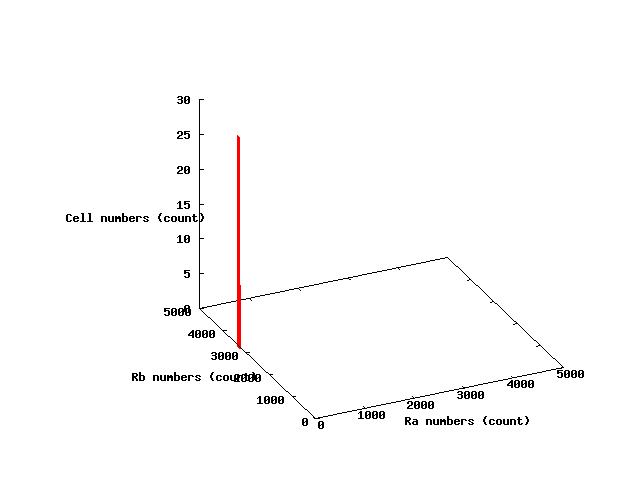
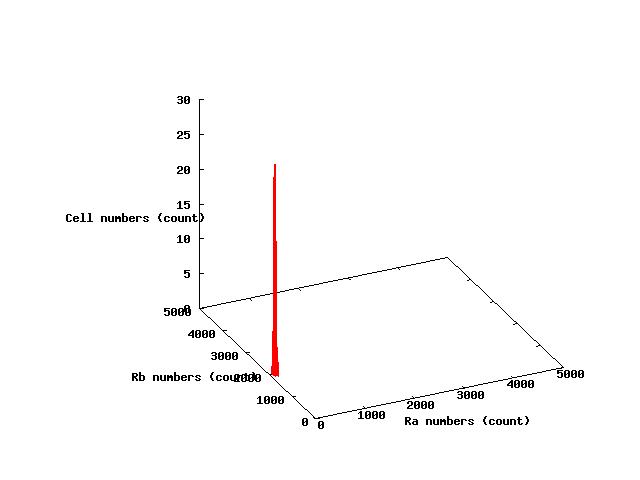
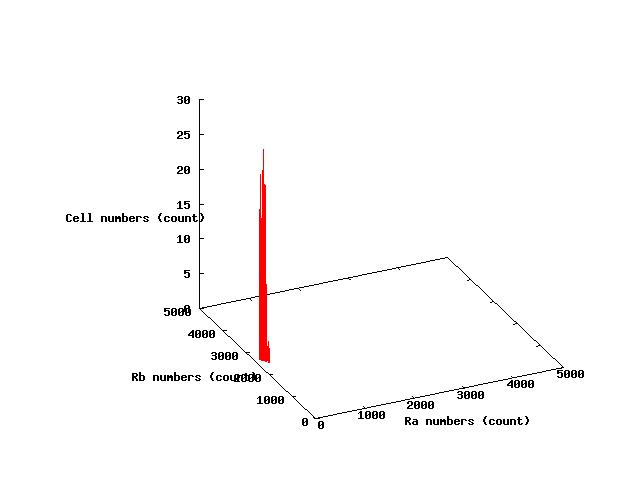
The values of parameters in the right table were used and the results of simulation were shown in Fig 5.1-3.



where α2 = 1(μM) in Fig 5.1,α2 = 2.7(μM) in Fig 5.2,α2 = 4(μM) in Fig 5.3. and it has been estimated that 1(μM) = 1000 molecules (count).


Fig.5.1 indicates that all cells shift to A state in the steady state and Fig 5.3 indicates that all cells shift to B state in the steady state.These results doesn't represent coexistence stable.
Fig.5.2 indicates that a portion of cells shift to A state and the others shift to B state in steady state;that is,individual cells are stable under stable coexistence.

Figure 5.1.A 　t=0.2(min)
Arrow2.JPG
Figure 5.1.B 　t=0.8(min)
Arrow2.JPG
Figure 5.1.C 　 t=30(min)　only A

movie here!!


Figure 5.2.A 　t=0.2(min)
Arrow2.JPG
Figure 5.2.B 　 t=0.8(min)
Arrow2.JPG
Figure 5.2.C 　 t=30(min)　　success!! coexistence

movie here!!


Figure 5.3.A 　 t=0.2(min)
Arrow2.JPG
Figure 5.3.B 　 t=0.8(min)
Arrow2.JPG
Figure 5.3.C 　 t=30(min)　　 only B

movie here!!


Next，the relation between the results of simulation and phase plane are shown in Fig.5.4.1-3,where the nullclines of this system were Ex 4-3

Figure 5.4.1
Figure 5.4.2
Figure 5.4.3


Fig.5.4.1-3 indicate that the distribution of the cells corresponds with the stable equilibrium points.

Retrieved from "http://2007.igem.org/wiki/index.php/Tokyo/Formulation/5.stochastic_differential_equation_model_with_poisson_random_variables"