Bangalore

The official wiki of the NCBS iGEM 2007 Team

Our team at the National Centre for Biological Sciences, Bangalore comprises undergraduate and graduate students from diverse backgrounds of science. We have gathered together to collectively investigate Multistability and Hysteresis in the Combinatorial Synthetic Vibrio Quorum Sensing Circuits designed by us.

We have designed a Mathematical Model for our circuits and are simultaneously carrying out a corresponding set of experiments using the bacterial strain E.coli-K12Z1.

It has been shown (Angeli et al) that for a class of feedback systems of arbitrary order, the stability properties and bifurcation diagram of the system can be deduced mathematically from how the system behaves when feedback is blocked. The system is guaranteed to be bistable for some range of feedback strengths provided the feedback-blocked system is monotone and shows a sigmoidal characteristic.

We have taken the Vibrio Quorum Sensing System. In this system, when the population density and hence the concentration of autoinducer (the messenger chemical produced in the cell) crosses a certain threshold, the expression of a set of genes that is required for bioluminescence is turned on. The production of the autoinducer is under the control of a gene, the expression of which involves positive feedback. The transcriptional regulator, LuxR* (which is a complex of LuxR and the autoinducer AI) governs the expression of the promoter, pR and we use CFP as the reporter here. Since the concentration of LuxR* depends on the concentrations of both AI and LuxR, we have a remarkable handle on the feedback of this system.

Note that this is a positive feedback system and its open loop can be closed in two different ways as shown in the following fig.

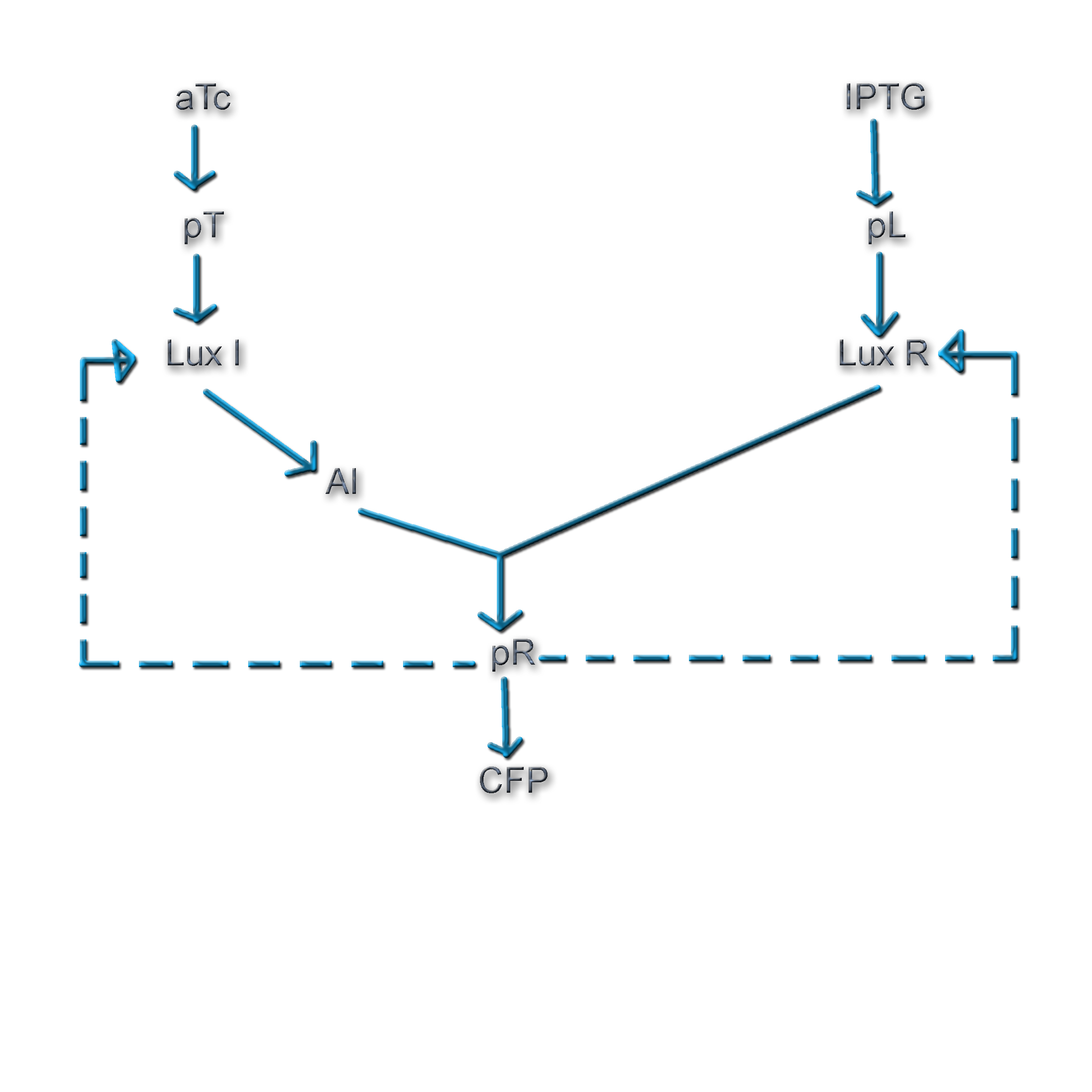Two ways in which the loop is closed.

Now we plan to check for the bistability of a similar synthetic genetic circuit constructed by us using various biobrick devices.

Our approach is to conduct a set of open loop experiments on the bacterial strain E-coli K12Z1. We vary the concentrations of AI and LuxR and get the I/O characteristic curves over a range obtained by varying the concentration of the corresponding inducers (aTc and IPTG). We quantify the expression levels for the genes at different stages by measuring the fluorescence intensities of CFP and YFP reporter proteins in the constructs using Fluorescence Microscopy.

The sigmoidal family of curves obtained from these open loop experiments when intersect with the superimposed equivalence line will give the steady states for the system. And thus the stability of these states will be concluded thereafter on the theorem proposed by Angeli et al.

For a detailed description of our project, the experimental design and the mathematical model, go to The Mission.