ETHZ/Simulation
From 2007.igem.org
(→Sensitivity Analysis) |
(→Sensitivity Analysis) |
||
| Line 113: | Line 113: | ||
In order for one to ensure a biological system will operate as it was modeled, he/she should understand the sensitivity of the system's behavior to all involved parameters. Due to the uncertainty in parameter retrieval, we would like our system to have reduced sensitivity to the parameters that are affected mostly by noise. That way, we can have a guaranteed stable performance, even under non-simulated conditions. | In order for one to ensure a biological system will operate as it was modeled, he/she should understand the sensitivity of the system's behavior to all involved parameters. Due to the uncertainty in parameter retrieval, we would like our system to have reduced sensitivity to the parameters that are affected mostly by noise. That way, we can have a guaranteed stable performance, even under non-simulated conditions. | ||
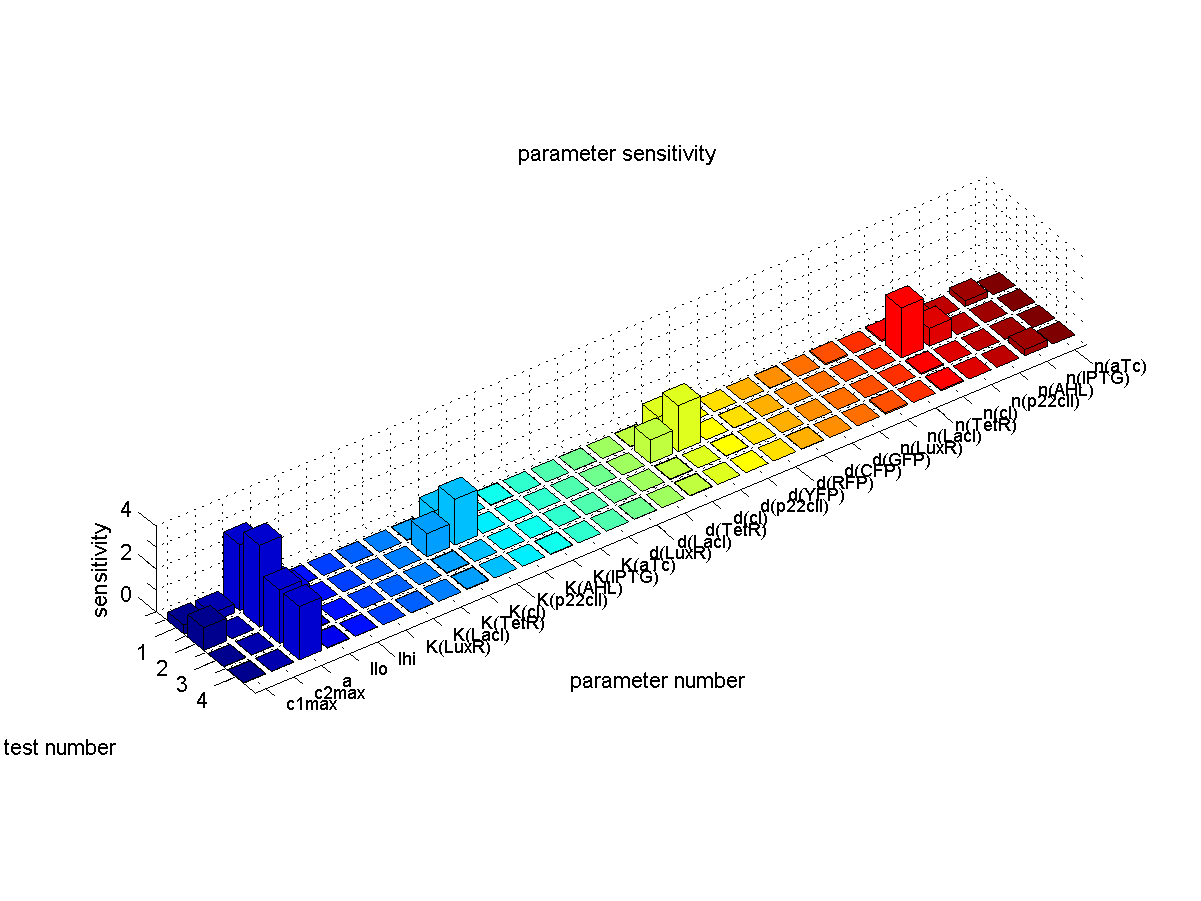
| - | [[Image:ETHZSensitivity.png|right|thumb|<b>Fig. | + | [[Image:ETHZSensitivity.png|right|thumb|<b>Fig. 6</b>: Sensitivity analysis. We plot the sensitivity for each parameter and each test case that corresponds to the different path ways in Fig. 1. |500px]] |
We simulated the behavior of our system throughout all its phases, while sweeping the parameters by 5%, one at a time. More specifically for the case presented in Fig. 1, we carried out the following procedure: | We simulated the behavior of our system throughout all its phases, while sweeping the parameters by 5%, one at a time. More specifically for the case presented in Fig. 1, we carried out the following procedure: | ||
For each parameter, we did the timing simulation as shown in Fig. 2. Once we increased the parameter by 5%, and once we decreased the parameter by 5%. Since in test case 1 (Fig. 2) we are interested in having a high concentration of CFP during the recognition phase with respect to the base line, we divide the steady state CFP concentration at 4000 minutes by the baseline concentration at 1000 minutes. Finally, as shown in the following equation, we define the sensitivity by subtracting the resulting factor that we get with an increased parameter, from the resulting factor that we get by a decreased parameter. | For each parameter, we did the timing simulation as shown in Fig. 2. Once we increased the parameter by 5%, and once we decreased the parameter by 5%. Since in test case 1 (Fig. 2) we are interested in having a high concentration of CFP during the recognition phase with respect to the base line, we divide the steady state CFP concentration at 4000 minutes by the baseline concentration at 1000 minutes. Finally, as shown in the following equation, we define the sensitivity by subtracting the resulting factor that we get with an increased parameter, from the resulting factor that we get by a decreased parameter. | ||
| - | [[Image:ETHZSensititivityequation.png|center| | + | [[Image:ETHZSensititivityequation.png|center|300px]] |
<!---<math>Sensitivity = \left | \frac{[ CFP^{105%}_{recognition} ] }{\left [ CFP^{105%}_{baseline}\right ] }- \frac{\left [ CFP^{95%}_{recognition} \right ] }{\left [ CFP^{95%}_{baseline} \right ] }\right |</math>---> | <!---<math>Sensitivity = \left | \frac{[ CFP^{105%}_{recognition} ] }{\left [ CFP^{105%}_{baseline}\right ] }- \frac{\left [ CFP^{95%}_{recognition} \right ] }{\left [ CFP^{95%}_{baseline} \right ] }\right |</math>---> | ||
| Line 124: | Line 124: | ||
We can summarize that, if there is no difference in the concentration of the desired output during the recognition phase with respect to baseline when sweeping a parameter by +/-5%, the sensitivity of that parameter is equal to zero. Otherwise the sensitivity gives us a measure of how much the concentration changes. | We can summarize that, if there is no difference in the concentration of the desired output during the recognition phase with respect to baseline when sweeping a parameter by +/-5%, the sensitivity of that parameter is equal to zero. Otherwise the sensitivity gives us a measure of how much the concentration changes. | ||
| - | We quantified the sensitivity for all parameters and all 4 test cases. The results are plotted in Fig. | + | We quantified the sensitivity for all parameters and all 4 test cases. The results are plotted in Fig. 6. |
The conclusions that can be derived from our sensitivity analysis are the following: | The conclusions that can be derived from our sensitivity analysis are the following: | ||
* Our system is most sensitive to the parameter "a", which describes the base production. This is not a surprising result, since we depend on having a good switch, and our signal-to-noise ratio, or output to baseline production level, depends highly on the fact that we can reliably switch off the production of the memory proteins cI and p22cII. For a more detailed analysis of the switching behavior please see our [[ETHZ/Biology | biological implementation]] page. | * Our system is most sensitive to the parameter "a", which describes the base production. This is not a surprising result, since we depend on having a good switch, and our signal-to-noise ratio, or output to baseline production level, depends highly on the fact that we can reliably switch off the production of the memory proteins cI and p22cII. For a more detailed analysis of the switching behavior please see our [[ETHZ/Biology | biological implementation]] page. | ||
* Other sensitive parameters are those that are directly related to the production and decay of the memory proteins cI and p22cII. This can be explained by the fact that our system prefers symmetry between the parameter sets of cI and p22cII, in order to support good switching behavior where the same concentration of p22cII leads to the same repression of cI and vice versa. We can especially see that those parameters seem to be more sensitive for the test cases 1 and 2, where cI has to be stored inside the memory. The reason for this behavior is due to the missing symmetry between the parameters for cI and p22cII, we currently have a bias inside the system towards the production of p22cII. | * Other sensitive parameters are those that are directly related to the production and decay of the memory proteins cI and p22cII. This can be explained by the fact that our system prefers symmetry between the parameter sets of cI and p22cII, in order to support good switching behavior where the same concentration of p22cII leads to the same repression of cI and vice versa. We can especially see that those parameters seem to be more sensitive for the test cases 1 and 2, where cI has to be stored inside the memory. The reason for this behavior is due to the missing symmetry between the parameters for cI and p22cII, we currently have a bias inside the system towards the production of p22cII. | ||
Revision as of 11:44, 23 October 2007

Introduction
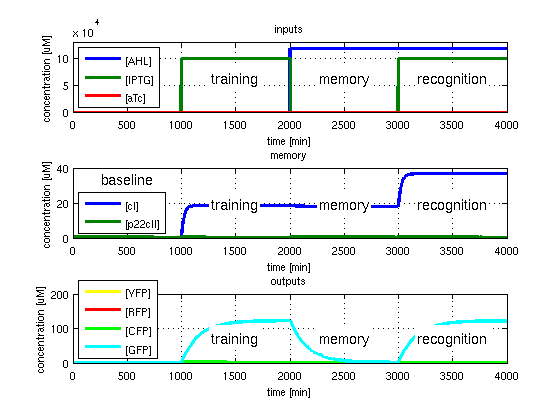
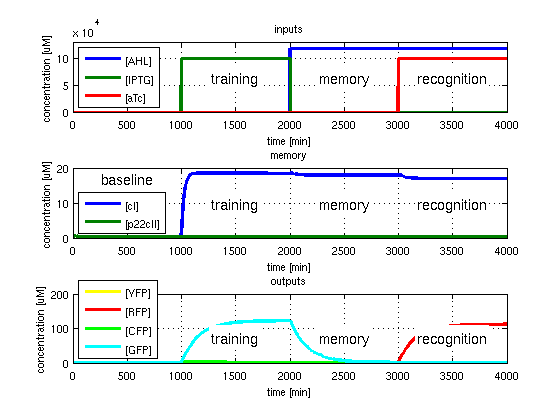
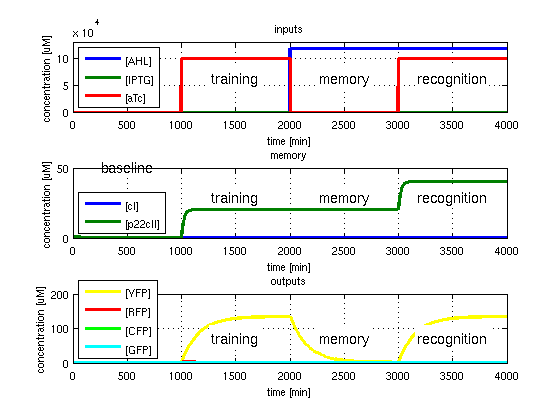
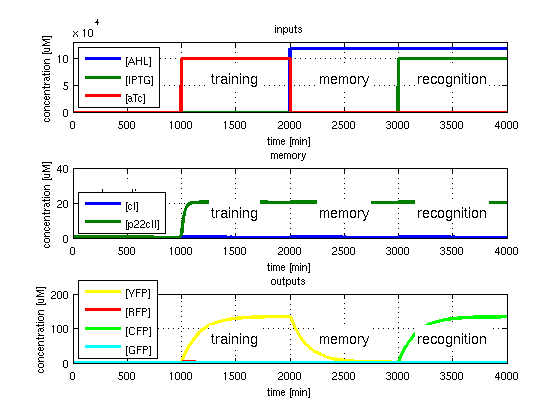
As has been presented in the Modeling page, we have created a model of our system that can be described as a finite state machine. In order to examine the behavior of our system thoroughly, we have to simulate it through all the difference phases that can be reached. We carry out our simulations based on the protocol presented in Fig. 1.
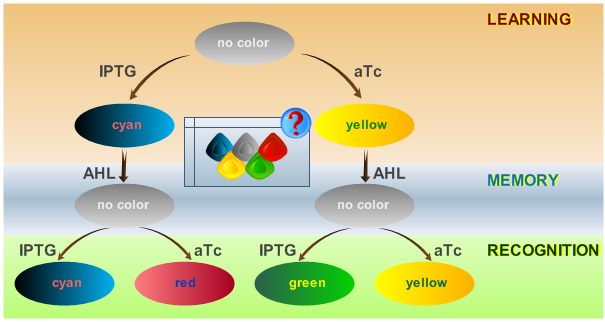
Simulation of Test Cases
To test all the possible conditions and transitions in our system, we run timing simulations for all 4 different branches in the flow diagram of our protocol, and we plot the concentrations of the inducers, memory proteins and reporter proteins. During each learning, memorizing and recognizing phase, we wait for the steady state of the system to be reached. The three phases of the system are thus separated sufficiently in time. In all the cases, we follow the following procedure:
- During the first 1000 minutes of the simulation, we do not add any inducers to the system, and as a result, we check for the baseline production of proteins.
- Between 1000 and 2000 minutes, we add the inducer that should be learned, and we let the system reach steady state.
- After 2000 minutes, we add the inducer AHL for memory formation, and run the simulation for an additional 1000 minutes, to reach again steady state.
- Between 3000 and 4000 minutes, we test the final behavior of the system, and check if it reacts in the desired way, by showing the appropriate color.
The parameters of the system are crucial if one wants to have accurate and realistic simulations. We present the parameters used to simulate our system, in the section Parameters.
Sensitivity Analysis
In order for one to ensure a biological system will operate as it was modeled, he/she should understand the sensitivity of the system's behavior to all involved parameters. Due to the uncertainty in parameter retrieval, we would like our system to have reduced sensitivity to the parameters that are affected mostly by noise. That way, we can have a guaranteed stable performance, even under non-simulated conditions.
We simulated the behavior of our system throughout all its phases, while sweeping the parameters by 5%, one at a time. More specifically for the case presented in Fig. 1, we carried out the following procedure: For each parameter, we did the timing simulation as shown in Fig. 2. Once we increased the parameter by 5%, and once we decreased the parameter by 5%. Since in test case 1 (Fig. 2) we are interested in having a high concentration of CFP during the recognition phase with respect to the base line, we divide the steady state CFP concentration at 4000 minutes by the baseline concentration at 1000 minutes. Finally, as shown in the following equation, we define the sensitivity by subtracting the resulting factor that we get with an increased parameter, from the resulting factor that we get by a decreased parameter.
We can summarize that, if there is no difference in the concentration of the desired output during the recognition phase with respect to baseline when sweeping a parameter by +/-5%, the sensitivity of that parameter is equal to zero. Otherwise the sensitivity gives us a measure of how much the concentration changes.
We quantified the sensitivity for all parameters and all 4 test cases. The results are plotted in Fig. 6.
The conclusions that can be derived from our sensitivity analysis are the following:
- Our system is most sensitive to the parameter "a", which describes the base production. This is not a surprising result, since we depend on having a good switch, and our signal-to-noise ratio, or output to baseline production level, depends highly on the fact that we can reliably switch off the production of the memory proteins cI and p22cII. For a more detailed analysis of the switching behavior please see our biological implementation page.
- Other sensitive parameters are those that are directly related to the production and decay of the memory proteins cI and p22cII. This can be explained by the fact that our system prefers symmetry between the parameter sets of cI and p22cII, in order to support good switching behavior where the same concentration of p22cII leads to the same repression of cI and vice versa. We can especially see that those parameters seem to be more sensitive for the test cases 1 and 2, where cI has to be stored inside the memory. The reason for this behavior is due to the missing symmetry between the parameters for cI and p22cII, we currently have a bias inside the system towards the production of p22cII.