USTC/OperatorComposition
From 2007.igem.org
Naming Rules for Oxx and Oxy below
Generally, Lac repressor bind to its operator in the form of dimer [1]. Almost all the according operators in nature are of approximate reverse symmetric structure, that is, each half of the operators consists of about 10 nucleotides and receives the binding of a repressor monomer [2]. It has been reported that it is the perfectly symmetric operator that most tightly binds to native Lac repressor. Based on this fact, an idea was proposed that the binding affinity of a non-symmetric operator might be systematically reduced, exempt from the harm on the binding specificity of the repressor-operator pairs.
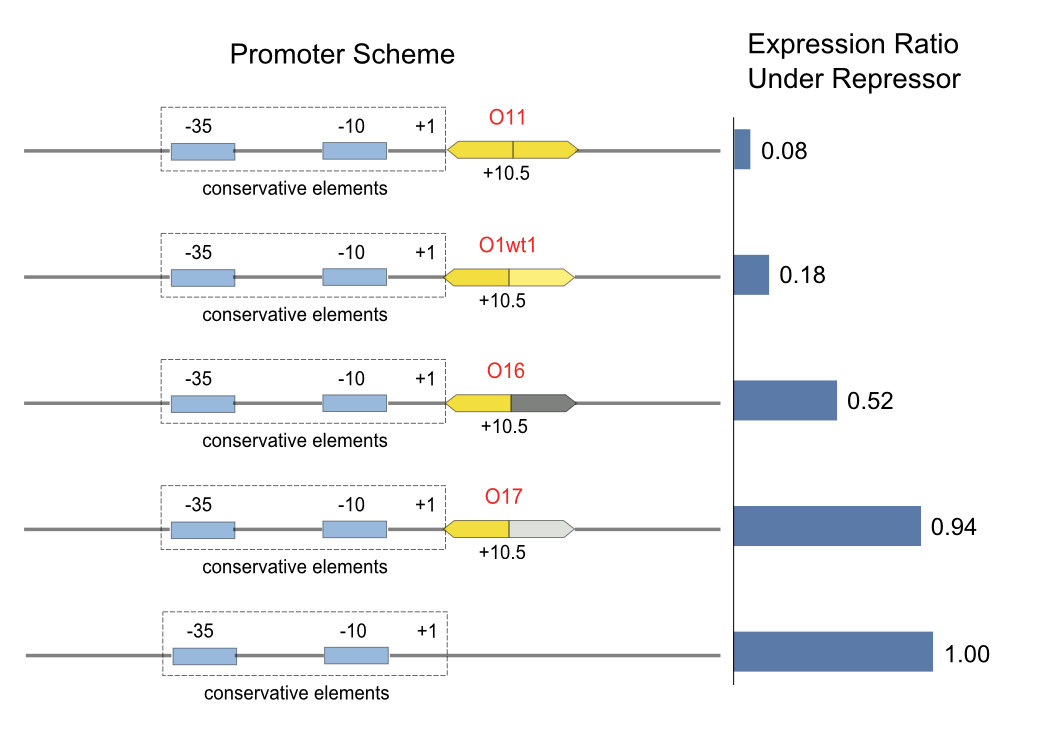
Five promoters have been synthesized for testing the effect of weakening. Three of them are based on O11 operator:
- O11, the perfectly symmetric operator in this five ones
- O1wt1, the native lac operator at +11 site of Plac promoter
- O16, the right half of O11 replaced by the right half of O66
- O17, the right half of O11 replaced by the right half of O77
- NUL, the positive control as intensity 1.00
(more details about Ox6 and Ox7)
After a series of our experiments (refer to Figure 1 whose data were from fluorescent measurement), we came to the conclusion that the method of replacing the right half of the symmetric operator can systematically reduce the binding affinity. Ox6, which means the right half of a symmetric operator is replaced by a weak operator sequence with the same pattern, can be used as a "weak" operator. At the same time, we found that the pattern Ox7 is weaker than that of Ox6, and the affinity of Ox7 is too low for a logic gate.
Actually, we've made up O61, the left half of O11 replaced by the left half of O66, but we found that it has no special feature compared with O16 according to data. For predigestion, we discard "O6x" series in the next works.
References
1. Lewis, M. (2005), 'The lac repressor.', C R Biol 328 (6), 521--548.
2. John R. Sadler, Henri Sasmor, and Joan L. Betz, A perfectly symmetric lac operator binds the lac repressor very tightly. PNAS Vol. 80, pp. 6785-6789, November 1983