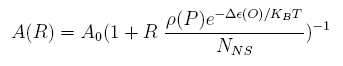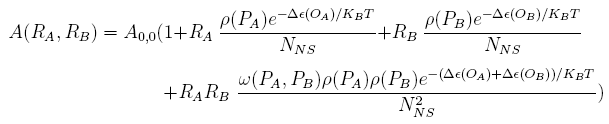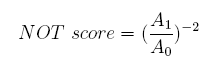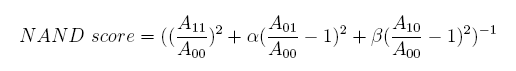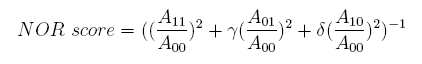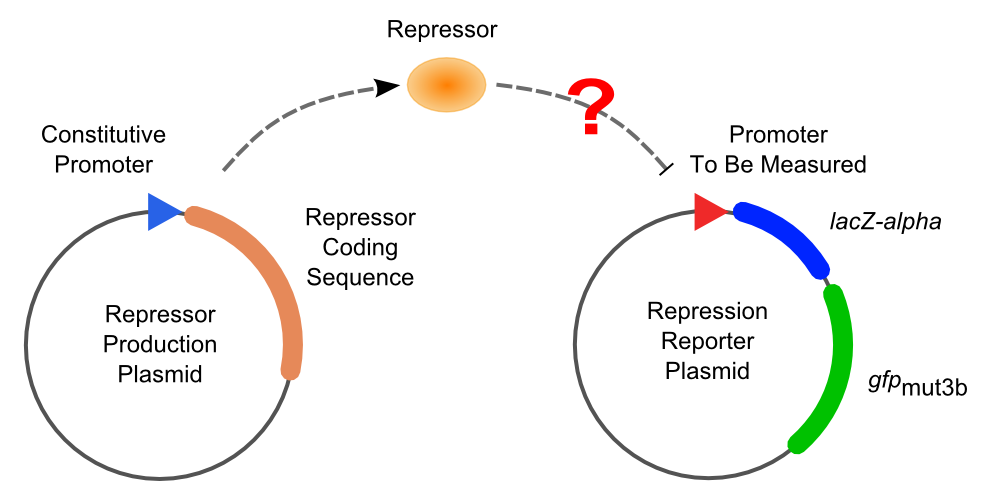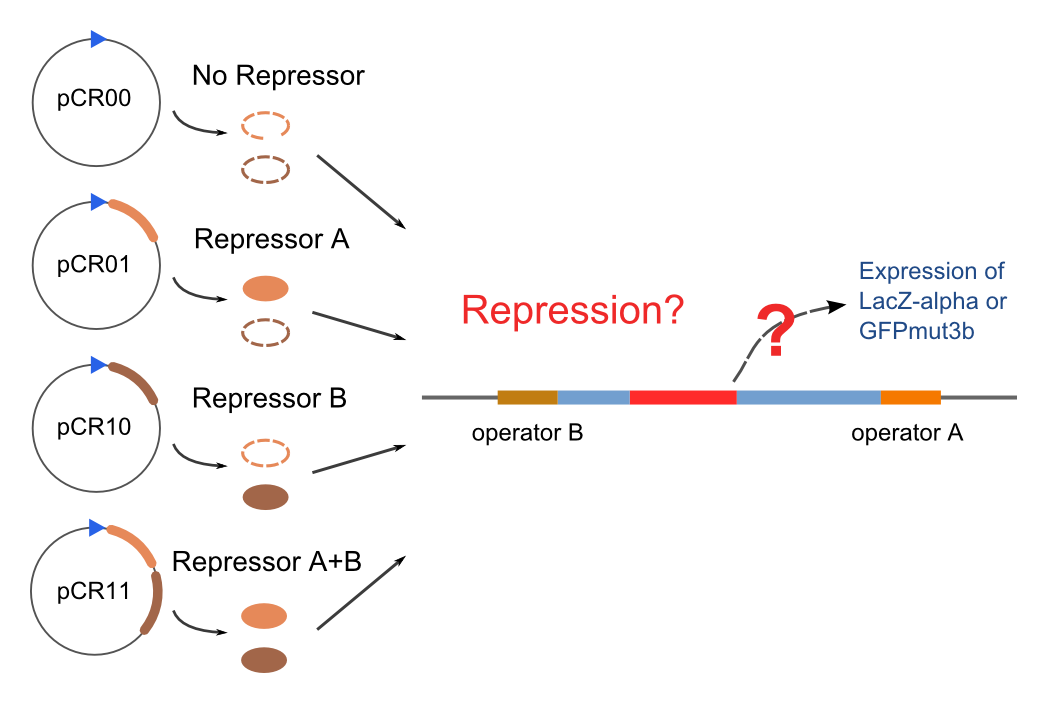USTC/Logic-Gate Promoters
From 2007.igem.org
m (→Build Up Promoter Family) |
m (→References) |
||
| Line 220: | Line 220: | ||
11. Sheridan, S. D.; Opel, M. L. & Hatfield, G. W. (2001), 'Activation and repression of transcription initiation by a distant DNA structural transition.', <i>Mol Microbiol</i> 40(3), 684--690. | 11. Sheridan, S. D.; Opel, M. L. & Hatfield, G. W. (2001), 'Activation and repression of transcription initiation by a distant DNA structural transition.', <i>Mol Microbiol</i> 40(3), 684--690. | ||
| + | |||
| + | 12. [http://cnse.albany.edu/News/index.cfm?step=show_detail&NewsID=424 Semiconductor International: 45 to 32 nm: Another Evolutionary Transition.] | ||
Revision as of 07:56, 25 October 2007
Contents |
Cis-acting Bio-Logic Gates
In natural cells, combinational logic computation can be carried out by cis-acting elements [4]. Theoretically, dual repressors interacting on two adjacent operators can generate complex logic function as NAND, NOT and NOT [1,2,3]. But seldom of the parameters of these models have been measured, and practical artificial logic promoters are hard to made because of the lack of appropriate inputs. In this project, we simplify these models to reduce the number of parameters, use artificial high-specific repressors based-on Lac repressor [8] as inputs, predict possible pattern of logic promoters, construct and test them experimentally, to attempt to find a systematical way to construct cis-acting bio-logic promoters. As the results, a piece of DNA about 60 – 200bp is able to be built up and to act as a logic gate.
Advatanges of Cis-acting Bio-Logic Gates
- Work in vivo and can be genetically inherited
- Can be systematically built up according to several patterns
- Small in scale
- About 2.0nm in width, 20 - 70nm in length, similar to transistors in present VSLI in size [12], sometimes even smaller
- Can be cascaded to implement any complex combinational logic computation
- And is also able to form sequential circuit
Repression Model
Lacramioara Bintu et al. have reported a simple thermodynamic model which can quantitatively describe promoter activity under one or more regulator factors [1,2]. In this project, we focus on fold-change under one or two repressors, which means the ratio of promoter activity in the absence and presence of repressor. For a weak promoter, the fold-change can be written approximately as a function of repressor concentrations, inter-operator distances, repressor–operator affinity and repressor-repressor interactions.
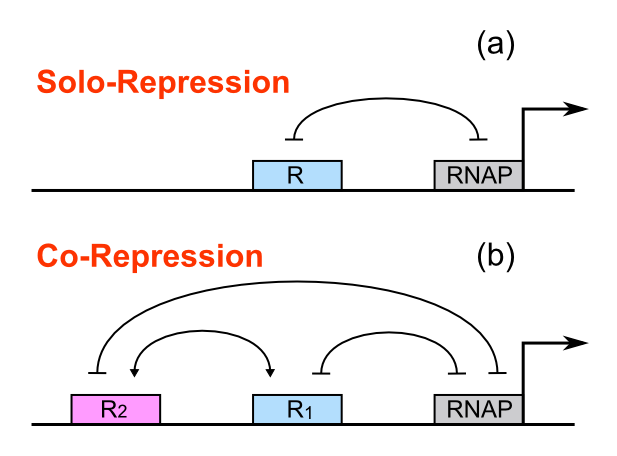
For a promoter containing a single operator site shown in Figure 1(a), the promoter activity under R repressor molecules A(R) is:
Where A(0) is the promoter activity without repression; ρ(P) is the solo-repression coefficient of the operator at the position P; Δε(O) is the binding energy difference of operator O on specific sites to non-specific sites; NNS is the number of non-specific sites; and KB means the Boltzmann constant, T is the temperature.
For a promoter containing two different operators, of which the relative repressors may be able to interact with each other shown in Figure 1(b), the promoter activity under combinations of two repressors, RA and RB, is given as:
Where ω(PA, PB) is the co-repression coefficient when OA is located at A, and OB at PB.
Concerning a NOT gate which works under approximate equal high and low repressor concentration, Rlow=0 and Rhigh=RH, its performance can be expressed simply as NOT score in a non-dimension form:
In the same way, NAND score and NOR score are:
For a fixed combination of two repressors, RA and RB, and approximate equal high and low repressor concentration, the logic performance of a promoter is a function of inter-operator distances, repressor–operator affinity and repressor-repressor interactions. By adjusting these parameters, it is possible to find out high-performance bio-logic promoters.
Schemes of Bio-Logic Promoters
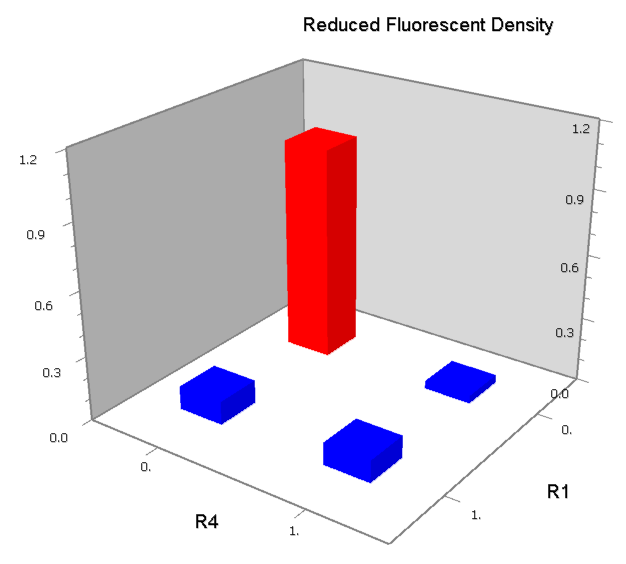
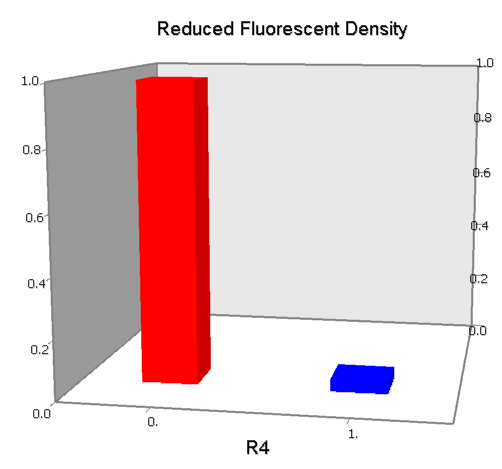
Dozens of potential bio-logic patterns were experimentally synthesized and tested in solo-repression or co-repression test-bench. Some representative ones are shown and commented as following.
Experiences for Bio-Logic Promoters
Composition of Operator USTC/OperatorComposition
Position of Operator USTC/OperatorPosition
Inter-operator Distance USTC/InterOperatorDistance
Hybrid Operator USTC/HybridOperator
Co-repressed Operator USTC/CoRepressedOperator
Repression Assay
Build Up Promoter Family
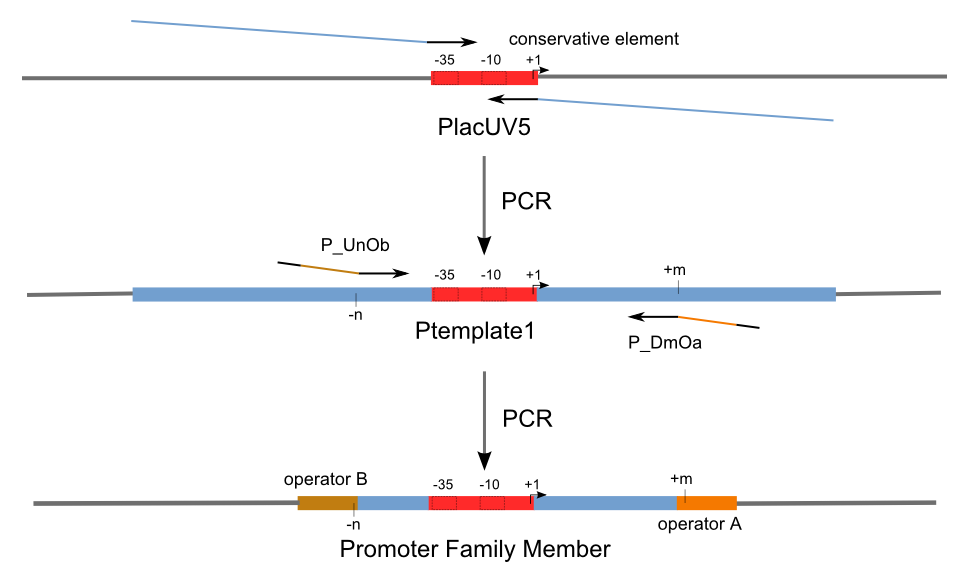
Firstly, we extend both sides of the conservative region for transcriptional initiation [9] of PlacUV5 [7], including -35 box,-10 box and +1 starting point, with two non-sense sequence selected from random groups. The product is named as P_template1 as it is the template for the promoter family. These two non-sense sequence have three main characters:
- They will never include the restriction enzyme cutting sites that will be involved in the whole study;
- They will never include the recognition sites of RNA Polymerases and those of either of the two repressors;
- They will never present in complicated structures.
Secondly, another group of primers, of which the elongation region at 5’ end may contain a unique operator sequence or each, is applied at both ends of P_template1, equipping us with an according group of promoters with complete structures. These promoters can include variant operator sequences at different position in flank of the conservative region.
Then the promoter fragments are digested with XbaI and BamHI and cloned into repression-reporter plasmid, which contains lacZ alpha fragment and gfp under the promoter insertion site.
Solo-Repression Assay
Two plasmids are used in solo-repression assay. First, a plasmid expressing a specific repressor constitutively is transformed into Top10. Then the promoters to be tested, which contain variant operator compositions and positions, are transformed into the strain got into the first step and selected by double resistances.
Co-Repression Assay
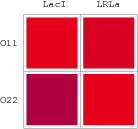
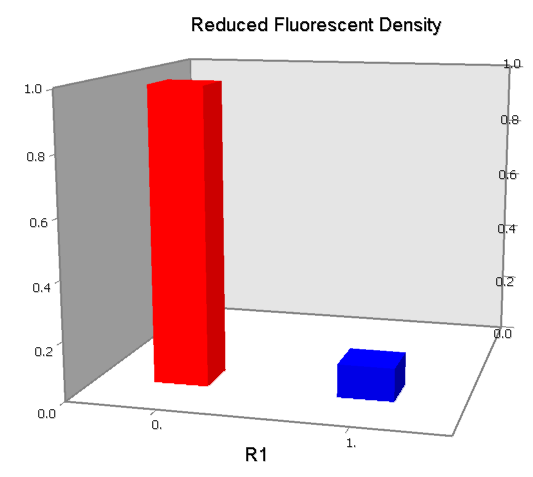
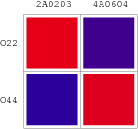
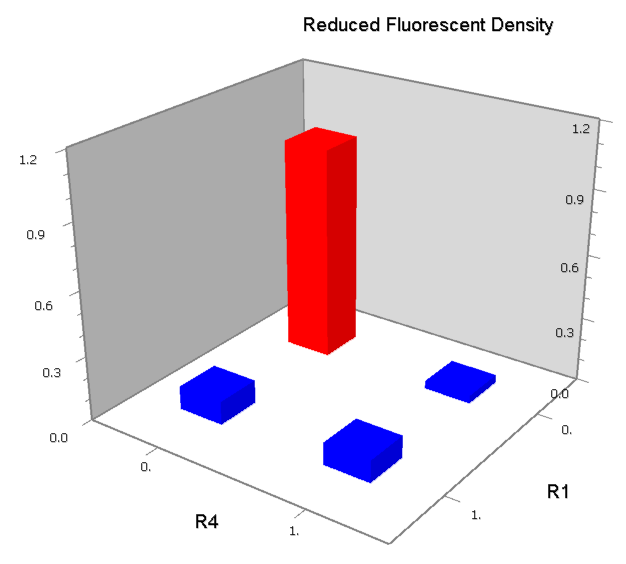
Promoters to be tested are cloned into double-reporter plasmid and then transformed into the four test strains (CR00, CR01, CR10, CR11). By reading the color of the colonies on plates with X-Gal, and by testing the fluorescence intensity under a fluorescence microscope, we can get the solo-repression and co-repression effects of the two repressors on specific promoters.
| Genotype | Character | Name |
| Top10/pT-TERM | So not express any repressors | CR00 |
| Top10/pT-ARL4A0604 | Constitutively express ARL4A0604 | CR01 |
| Top10/pT-ARL2A0203 | Constitutively express ARL2A0203 | CR10 |
| Top10/pTet-ARL4A0604-ARL2A203 | Constitutively express ARL4A0604 and ARL2A0203 | CR11 |
Final Results
Suggested Patterns
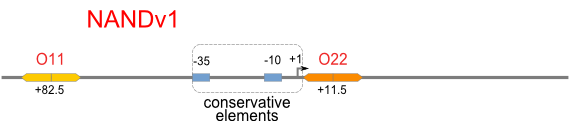
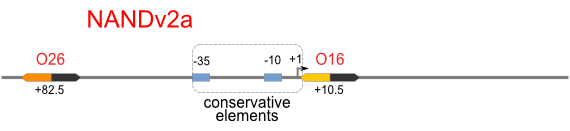
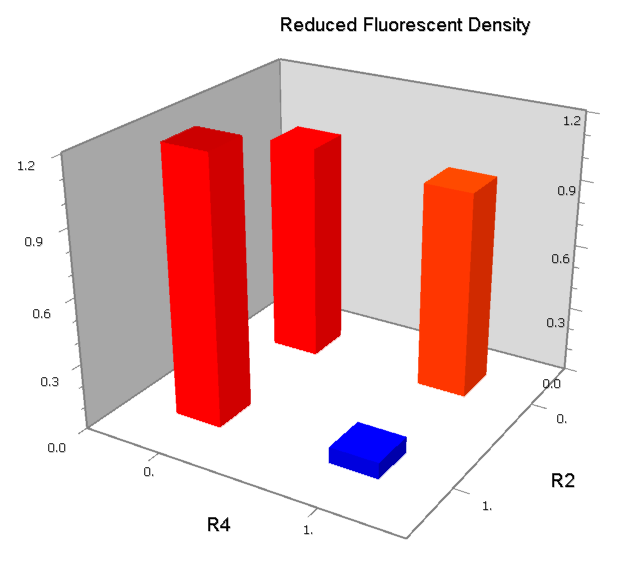
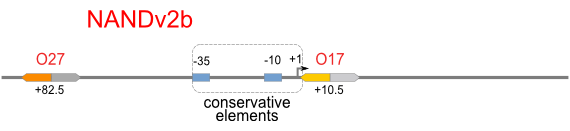
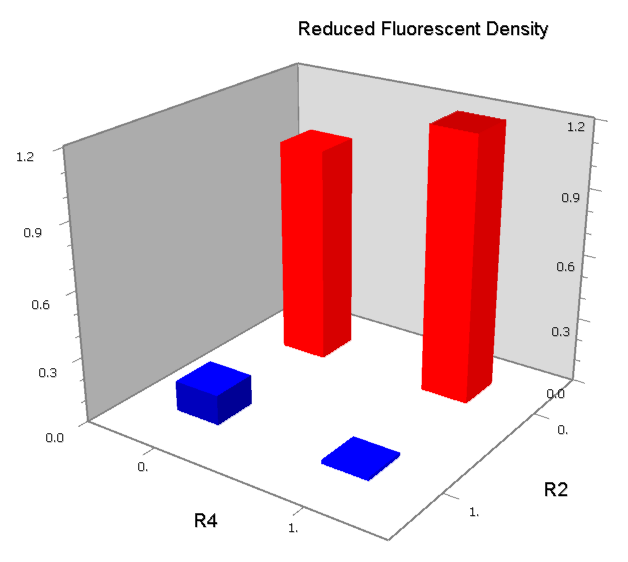
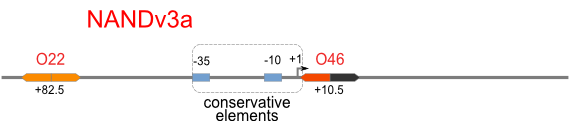
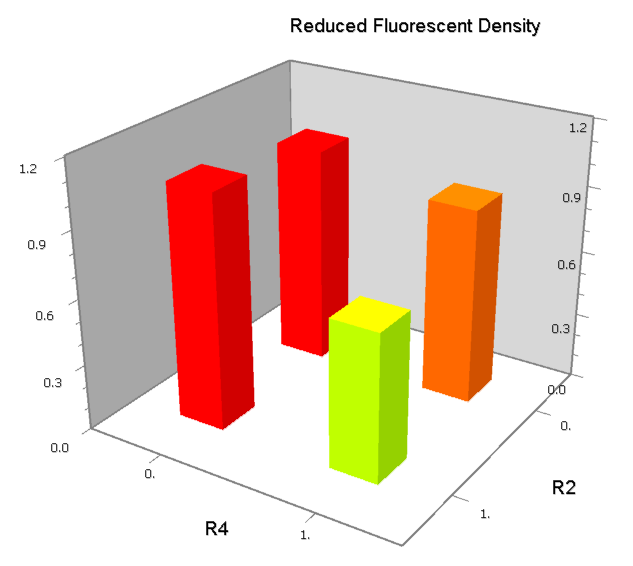
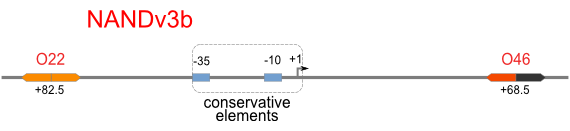
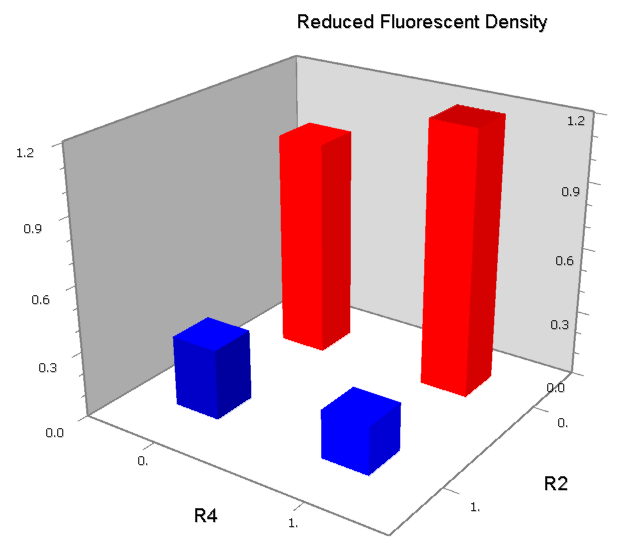
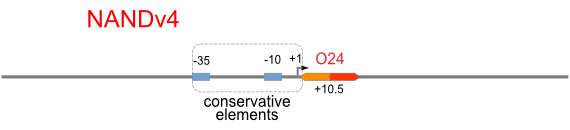
NAND
A NAND Gate requires that two solo-repressions should be weak, and co-repression should be strong. We choose +83.5 to put the upstream operator, to avoid the uncertain activator regions. Another weak operator is put down at the +66.5 site. The relative distance between the two operators is 150, indicating a strong co-repression.
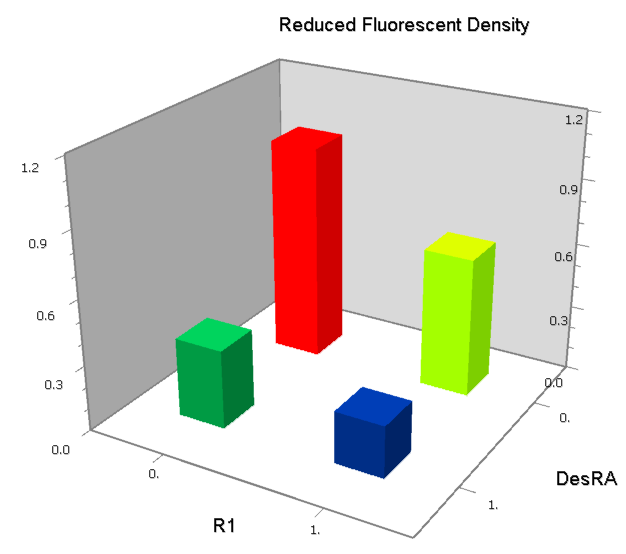
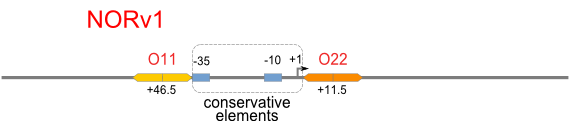
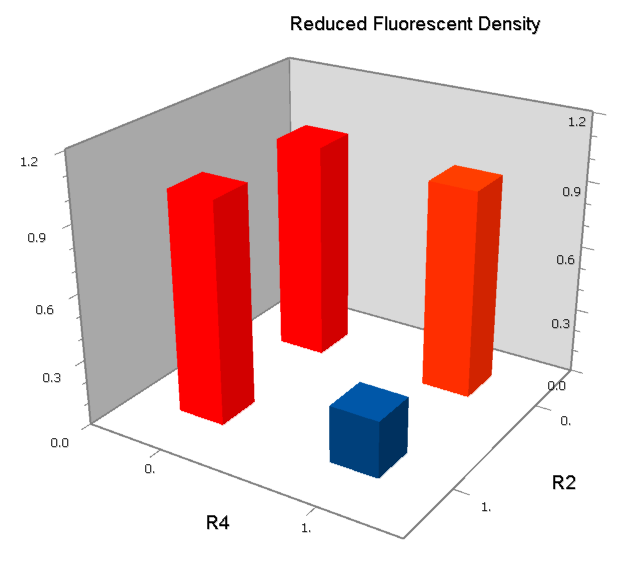
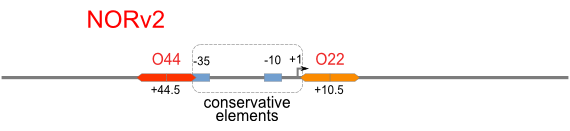
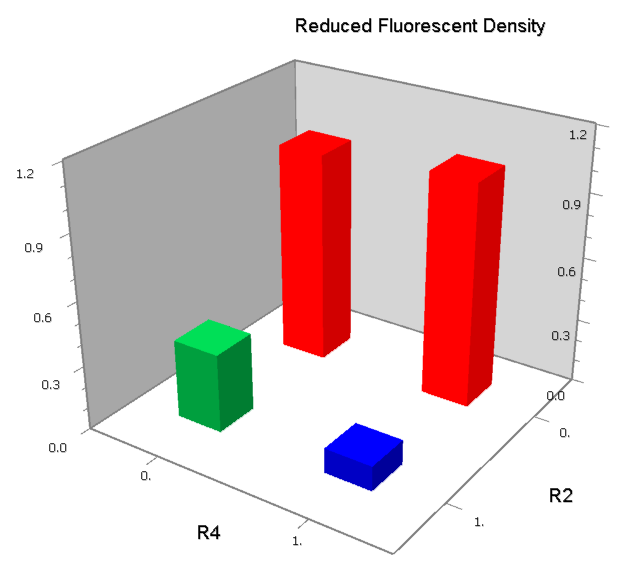
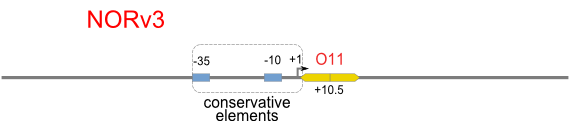
NOR
We expected to find a NOR gate with two different operators around the conservative region of a promoter. But there is no available repressor binding site in the upstream of the conservative region based on the observed effect of operator position. At present only the co-repressed pattern works well as NOR gate, but it brings in a limitation in integration.
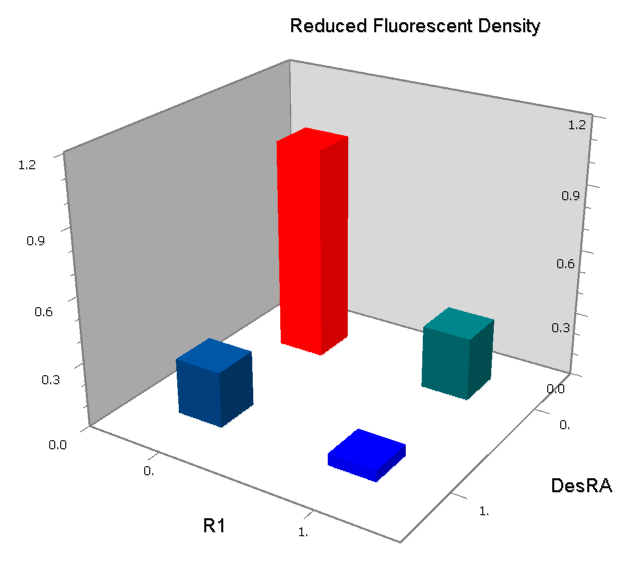
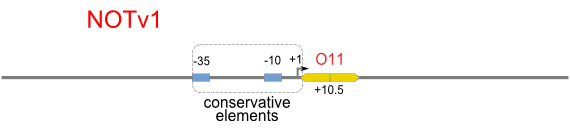
NOT
NOT gate is quite simple, only one symmetric operator at the +10.5 site.
References
1. Bintu, L.; Buchler, N. E.; Garcia, H. G.; Gerland, U.; Hwa, T.; Kondev, J.; Kuhlman, T. & Phillips, R. (2005), 'Transcriptional regulation by the numbers: applications.', Curr Opin Genet Dev 15(2), 125--135.
2. Bintu, L.; Buchler, N. E.; Garcia, H. G.; Gerland, U.; Hwa, T.; Kondev, J. & Phillips, R. (2005), 'Transcriptional regulation by the numbers: models.', Curr Opin Genet Dev 15(2), 116--124.
3. Buchler, N. E.; Gerland, U. & Hwa, T. (2003), 'On schemes of combinatorial transcription logic.', PNAS 100(9), 5136--5141.
4. Davidson, E. H.; Rast, J. P.; Oliveri, P.; Ransick, A.; Calestani, C.; Yuh, C.; Minokawa, T.; Amore, G.; Hinman, V.; Arenas-Mena, C.; Otim, O.; Brown, C. T.; Livi, C. B.; Lee, P. Y.; Revilla, R.; Rust, A. G.; jun Pan, Z.; Schilstra, M. J.; Clarke, P. J. C.; Arnone, M. I.; Rowen, L.; Cameron, R. A.; McClay, D. R.; Hood, L. & Bolouri, H. (2002), A genomic regulatory network for development., Science 295(5560), 1669--1678.
5. Elledge, S. J. & Davis, R. W. (1989), 'Position and density effects on repression by stationary and mobile DNA-binding proteins.', Genes Dev 3(2), 185--197.
6. Kalodimos, C. G.; Bonvin, A. M. J. J.; Salinas, R. K.; Wechselberger, R.; Boelens, R. & Kaptein, R. (2002), 'Plasticity in protein-DNA recognition: lac repressor interacts with its natural operator 01 through alternative conformations of its DNA-binding domain.', EMBO J 21(12), 2866--2876.
7. Lanzer, M. & Bujard, H. (1988), 'Promoters largely determine the efficiency of repressor action.', PNAS 85(23), 8973--8977.
8. Lewis, M. (2005), 'The lac repressor.', C R Biol 328(6), 521--548.
9. Rojo, F. (1999), 'Repression of transcription initiation in bacteria.', J Bacteriol 181(10), 2987--2991.
10. Saiz, L. & Vilar, J. M. G. (2006), 'DNA looping: the consequences and its control.', Curr Opin Struct Biol 16(3), 344--350.
11. Sheridan, S. D.; Opel, M. L. & Hatfield, G. W. (2001), 'Activation and repression of transcription initiation by a distant DNA structural transition.', Mol Microbiol 40(3), 684--690.
12. [http://cnse.albany.edu/News/index.cfm?step=show_detail&NewsID=424 Semiconductor International: 45 to 32 nm: Another Evolutionary Transition.]