From 2007.igem.org

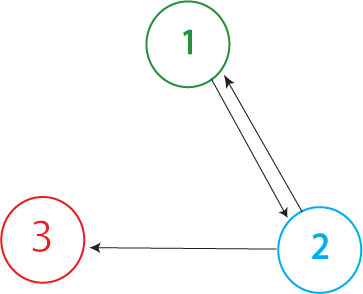
The Davidson team has proposed building the graph shown above in our first attempt at solving the Hamiltonian Path Problem in vivo. (The Missouri Western team will likely build a similar graph, with an edge from node 3 to node 1 but no edge from node 2 to node 1.) In order to determine if a Hamiltonian Path exists in the directed graph above, we propose a plasmid design similar to that shown below.

This cartoon represents a solved arangement of our proposed construct. Between the two pairs of BioBrick restriction enzyme sites lies a region containing three DNA fragments, each flanked by hixC sites (represented by the black, jagged rectangles). Each node of the graph represents one of the following genes: GFP (Green Fluorescent Protein), Kanamycin Resistance and a transcription terminator. Each edge of the graph is included in the construct between two hixC sites. In the presence of Hin protein, flipping of the edges at hixC sites will produce random walks through the graph. When flipped into the correct orientation and located upstream of any transcription terminators, a given gene will be transcribed upon promotion from the promoter region. All random walks through the graph will be generated through flipping. However, by using the inducible T7 promoter, no phenotypes will be displayed intially. Only in the presence of T7 RNA polymerase will the T7 promoter allow for transcription. This T7 system has been shown to transcribe long regions of DNA.

All plasmids (now containing random walks through the graph) will first be retransformed into new competent cells that lack Hin protein (and, therefore, their flipping mechanism). Instead, these cells will contain the plasmid shown in the image above, which produces T7 RNA polymerase.

T7 RNA polymerase is specific to the inducible T7 promoter on the Hamiltonian graph plasmid. Retransformation of the plasmids, therefore, has the dual effect of stopping flipping of edges and intializing transcription of all "solved" genes. The image above shows a solved plasmid post-retransformation. Both GFP and Kanamycin resistance would be expressed in this cell.

It is possible for all of the genes in the graph to be expressed (or all of the nodes to be visited), but for a Hamiltonian Path not to exist in the system. A "false positive" of this type is shown above. This path (1->2, 2->1, 2->3) through the graph is not allowed because it demands "teleportation" from node 1 to node 2, and it also visits nodes (2 and 1) multiple times. Because false positives require that at least one extra edge exist in the path through the graph (when compared to true solution of the Hamiltonian Path Problem), the true solution to the HPP will always contain the shortest DNA fragment between the promoter and the terminator of all the positive phenotypes. We will screen out any false positives through PCR and gel electrophoresis.