Tokyo/Works/Simulation
From 2007.igem.org
(→範囲の提示) |
(→範囲の提示) |
||
| Line 61: | Line 61: | ||
===範囲の提示=== | ===範囲の提示=== | ||
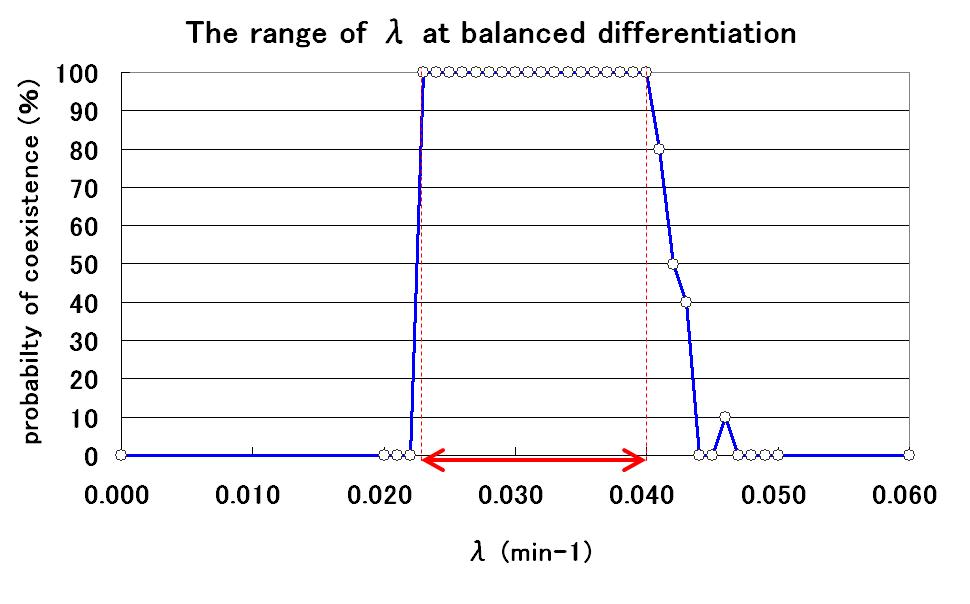
| - | <!--共存安定になるパラメータλの範囲を調べるため,λを変化させてシミュレーションをした.その結果,λの値とAとBが共存安定する確率の関係はFig.5のようになった.-->To determine the range of parameter λ, several simulations were conducted with different values of λ. As a result, the relationship between λ value and the probability of coexistence | + | <!--共存安定になるパラメータλの範囲を調べるため,λを変化させてシミュレーションをした.その結果,λの値とAとBが共存安定する確率の関係はFig.5のようになった.-->To determine the range of parameter λ, several simulations were conducted with different values of λ. As a result, the relationship between λ value and the probability of coexistence is determined as shown in Fig.5. |
[[Image:range_of_lambda.JPG|400px|thumb|none|Fig.5]] | [[Image:range_of_lambda.JPG|400px|thumb|none|Fig.5]] | ||
Revision as of 01:44, 26 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
What we have found so far
Wet experiments have determined Hill coefficients, coefficients of repression and activation of AHL and LacI(n2,n3,k2,k3) as follows.
n2 = 2.08 (-)
K2 = 4.05 (μM)
n3 = 2.47 (-)
K3 = 0.295 (μM)
共存安定になるようなパラメータ範囲の提示
共存安定状態の例
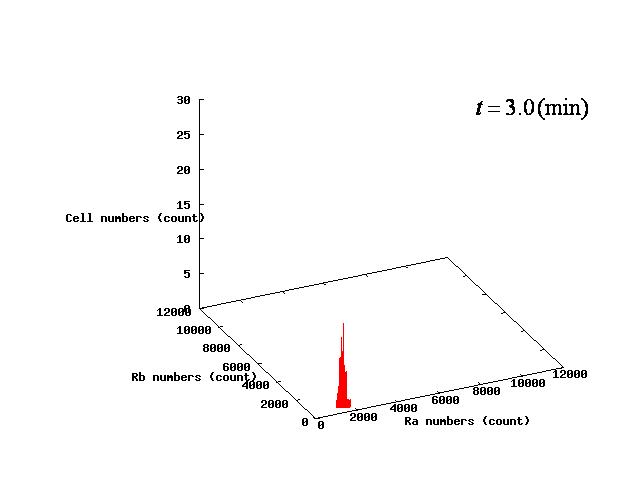
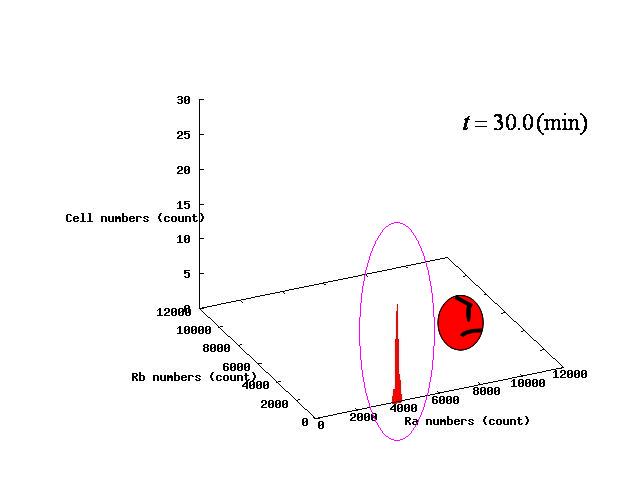
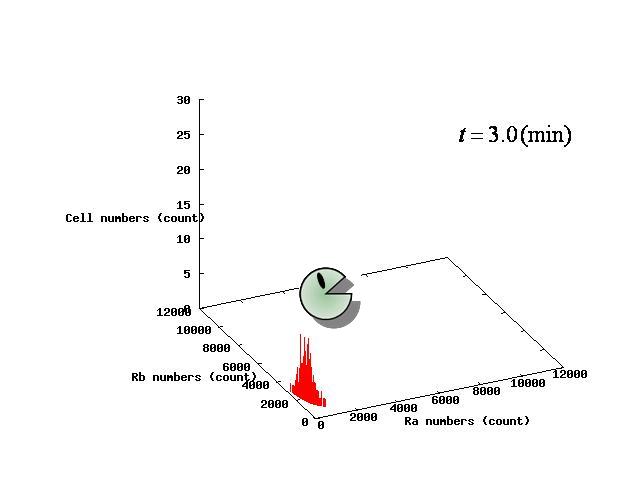
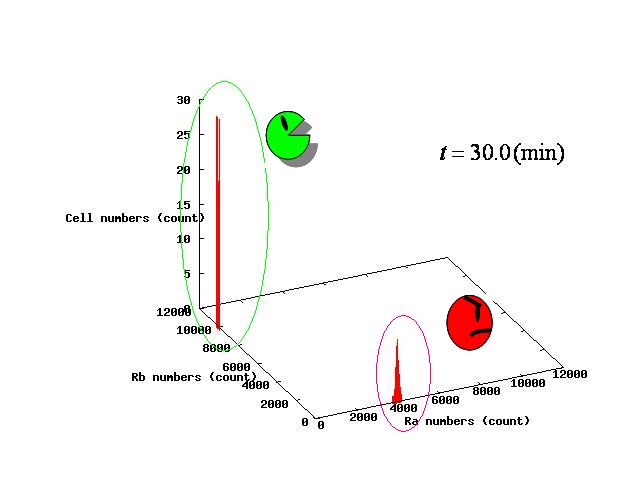
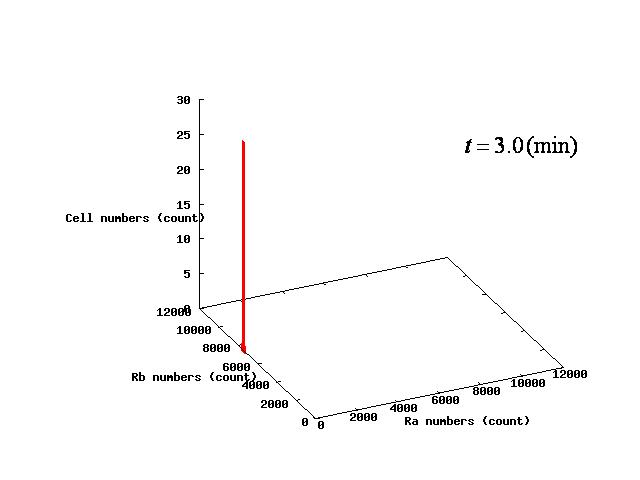
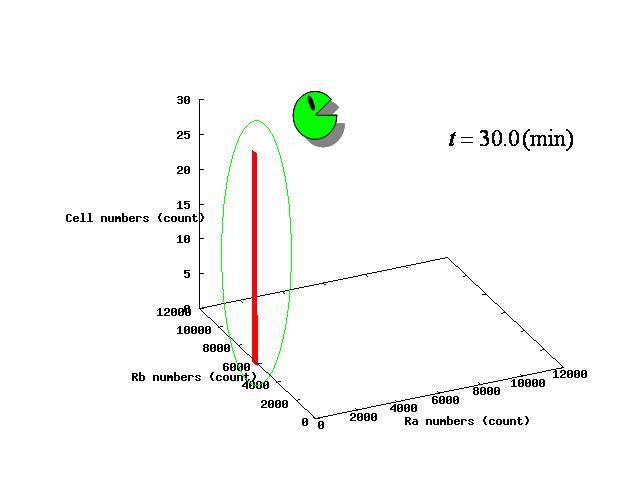
パラメータλの値によって,AとBが共存して安定する場合と,Aのみ,Bのみになってしまう3つのパターンが生じる. それぞれのパターンについてシミュレーション結果を示すとFig.1-3のようになる. Depending on the value of parameter λ, there are three different patterns:the stable coexistence of A and B pattern, only A pattern, and only B pattern. The simulation result in respect to each pattern is shown in Fig.1-3
⇒ movie here!!
⇒ movie here!!
⇒ movie here!!
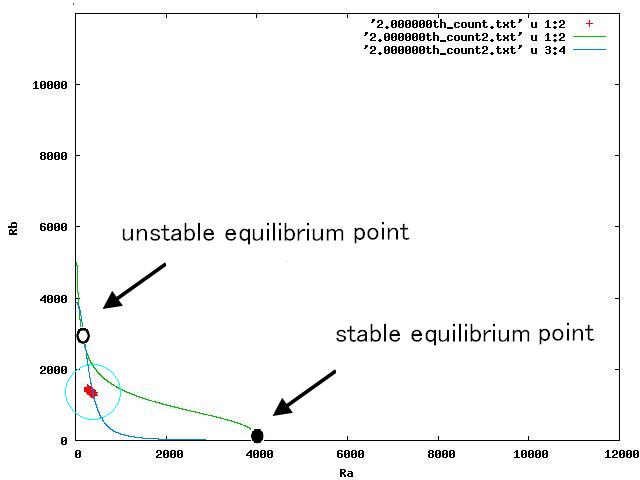
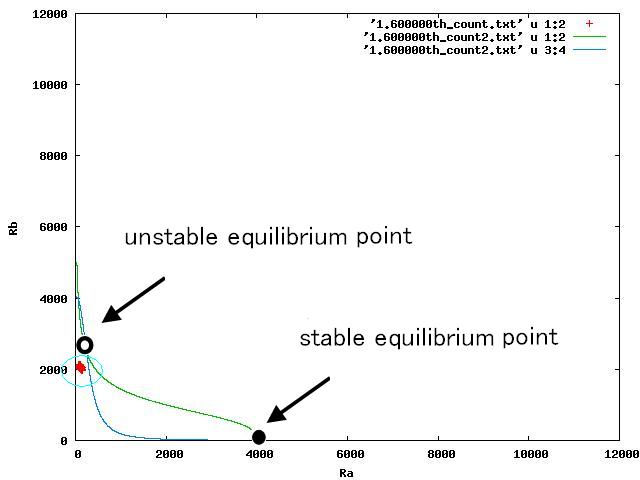
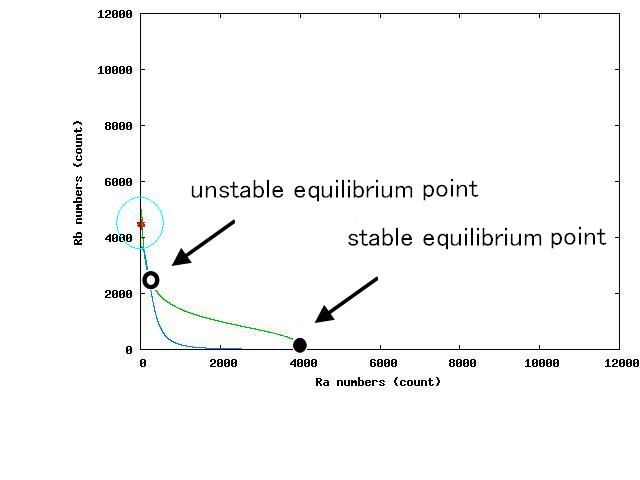
3パターンについて,nullclinesの交点が2つになる瞬間の相平面はFig.4.A-Cのようになる.
For the three patterns, the phase portraits at the moment when the number of the intersection of nullclines become two are shown in Fig.4.A-C respectively.
Fig.4.Aでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりA側に存在している.Fig.4.A shows that when the two equilibrium points appeared, cells were existing closer to A-side than the unstable equiblium point.
逆に,Fig.4.Cでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりもB側に存在している.
さらに,nullclineの交点が二つになった次の瞬間にはB側にも安定点が生じるので,Fig.4の時点で,A側に存在している場合は不安定平衡点を超えてB側に遷移することができなくなり,そのまま全てのセルがA側に遷移する.
逆に,cellsがB側に存在している場合は,不安定平衡点を越えてA側に遷移することが出来なくなり,そのまま全てのセルがB側に戻る.
次に,共存安定するFig.4.Bを見ると,不安定平衡点ができた瞬間にcelllsはその不安定平衡点付近に存在している.そしてB側にも安定点が生じた瞬間に,あるcellsはA側の安定点にシフトし,あるcellsはB側の安定点にシフトする.
⇒ movie about Fig.4.A here!!
⇒ movie about Fig.4.B here!!
⇒ movie about Fig.4.C here!!
範囲の提示
To determine the range of parameter λ, several simulations were conducted with different values of λ. As a result, the relationship between λ value and the probability of coexistence is determined as shown in Fig.5.
よって,パラメータλをこの範囲の中に入るように調節すれば,我々が目的としているモデルを作り出すことができる! By using parameter λ in this range, we can construct our model.