Tokyo/Works/Simulation
From 2007.igem.org
| Line 16: | Line 16: | ||
<!--パラメータλの値によって,AとBが共存して安定する場合と,Aのみ,Bのみになってしまう3つのパターンが生じる. | <!--パラメータλの値によって,AとBが共存して安定する場合と,Aのみ,Bのみになってしまう3つのパターンが生じる. | ||
それぞれのパターンについてシミュレーション結果を示すとFig.1-3のようになる.--> | それぞれのパターンについてシミュレーション結果を示すとFig.1-3のようになる.--> | ||
| - | [Image:3D_start.JPG|200px|left|thumb|Fig.1.A t=0.0(min)]] | + | [[Image:3D_start.JPG|200px|left|thumb|Fig.1.A t=0.0(min)]] |
[[Image:arrow2.JPG|50px|left|thumb]] | [[Image:arrow2.JPG|50px|left|thumb]] | ||
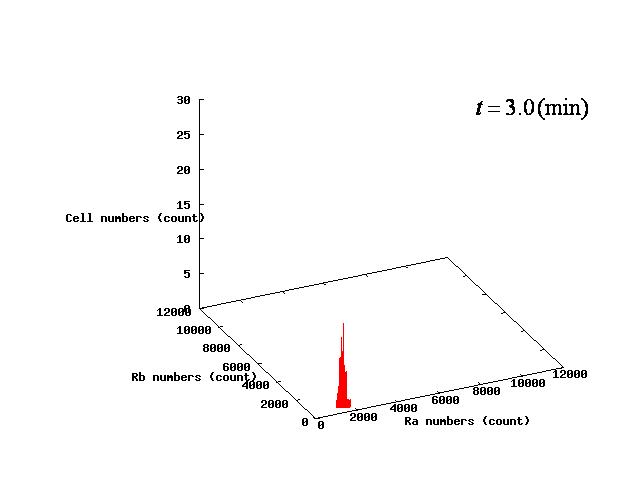
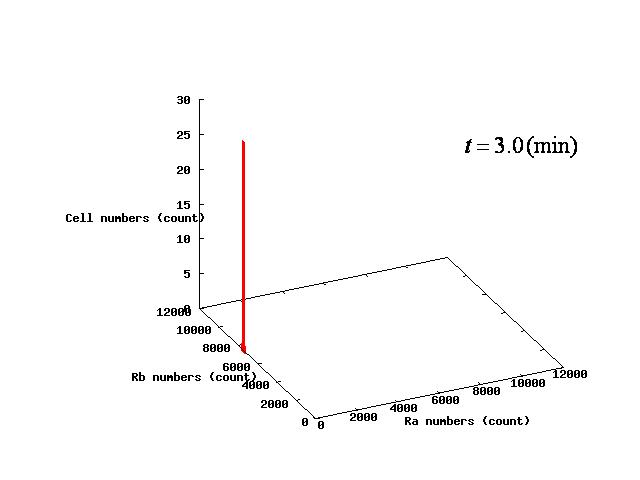
[[Image:3D_t3_a.JPG|200px|left|thumb|Fig.1.B t=3.0(min)]] | [[Image:3D_t3_a.JPG|200px|left|thumb|Fig.1.B t=3.0(min)]] | ||
Revision as of 11:40, 26 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
What we have found so far
Wet experiments have determined Hill coefficients, coefficients of repression and activation of AHL and LacI(n2,n3,k2,k3) as follows.
n2 = 2.08 (-)
K2 = 4.05 (μM)
n3 = 2.47 (-)
K3 = 0.295 (μM)
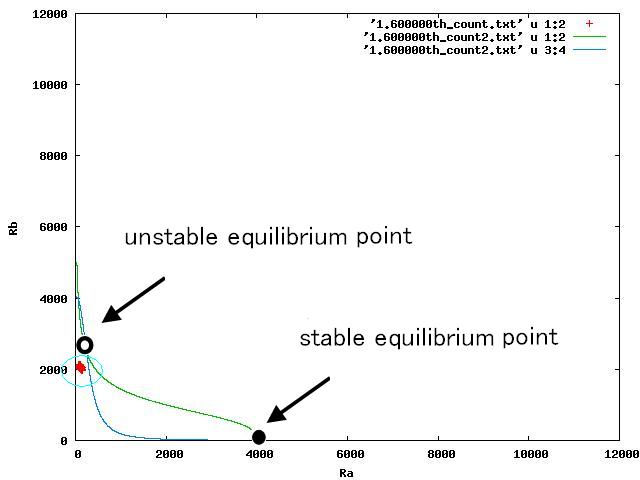
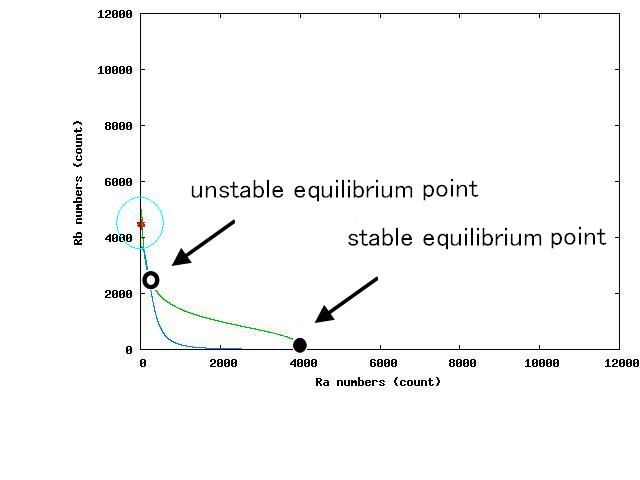
Determining the range of parameter which satisfy coexistent stability
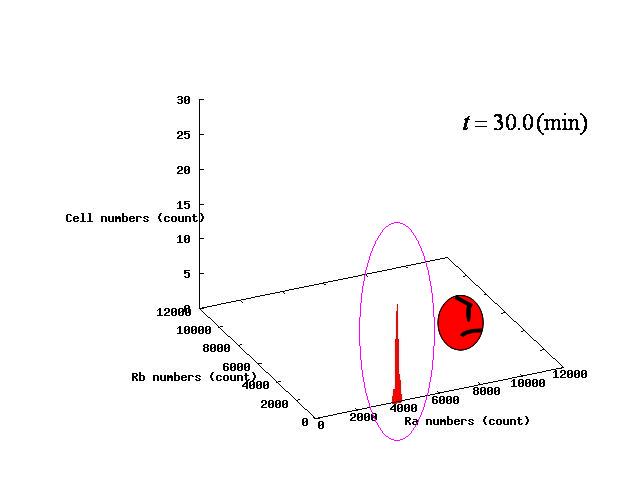
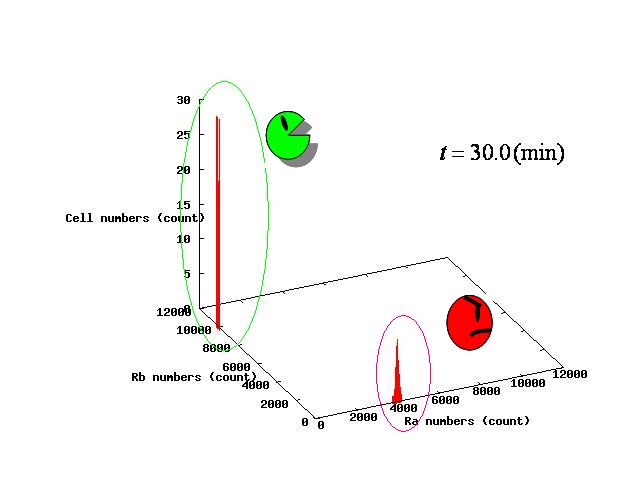
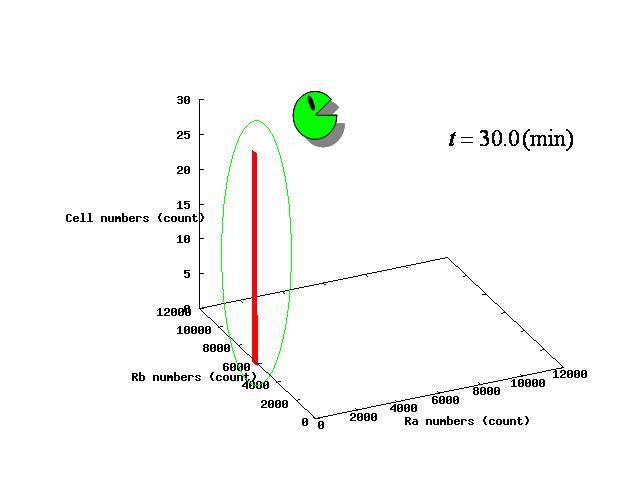
The example of coexistent stable state
⇒ movie here!!
⇒ movie here!!
⇒ movie here!!
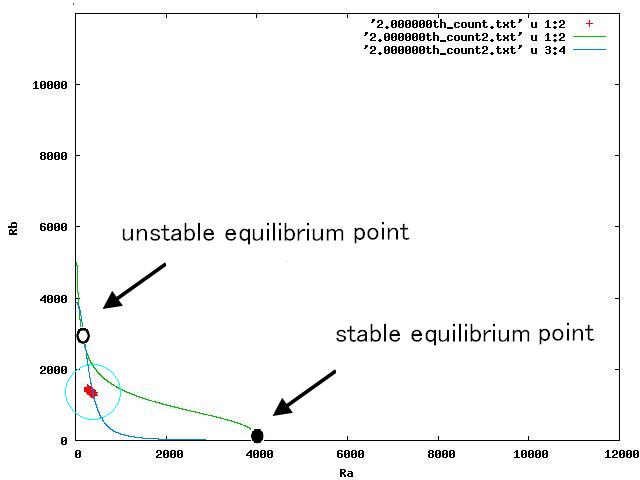
For the three patterns, the phase portraits at the moment when the number of the intersection of nullclines become two are shown in Fig.4.A-C respectively.
Fig.4.A shows that when the two equilibrium points appeared, cells were existing closer to A-side than the unstable equilibrium point. Oppositely,in Fig.4.C,when the two equilibrium points appeared, cells were existing closer to A-side than the unstable equiliblium point. Since when the number of the intersection of nullclines becomes two, stable point appears on B-side, at the moment of Fig.4, cells on the A-side cannot transit to B-side across unstble equilibrium point. As a result, all cells transit to A-side.
⇒ movie about Fig.4.A here!!
⇒ movie about Fig.4.B here!!
⇒ movie about Fig.4.C here!!
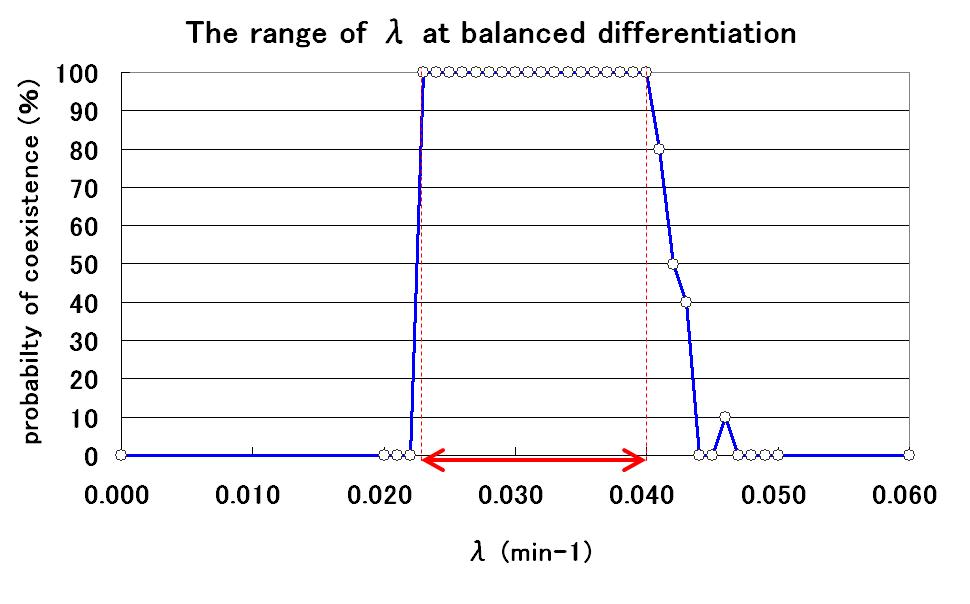
The range of parameter λ
To determine the range of parameter λ, several simulations were conducted with different values of λ. As a result, the relationship between λ value and the probability of coexistence is determined as shown in Fig.5.
By using parameter λ in this range, we can construct our model.