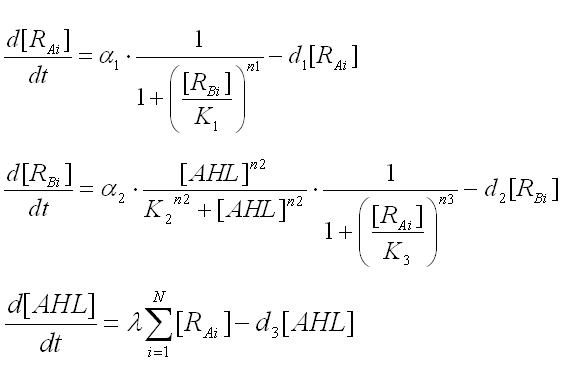Tokyo/Works/Simulation
From 2007.igem.org
(→シミュレーションはpopulationモデルに拡張し,確率微分方程式を用いた) |
|||
| Line 4: | Line 4: | ||
<!--==ここまでわかったこと==--> | <!--==ここまでわかったこと==--> | ||
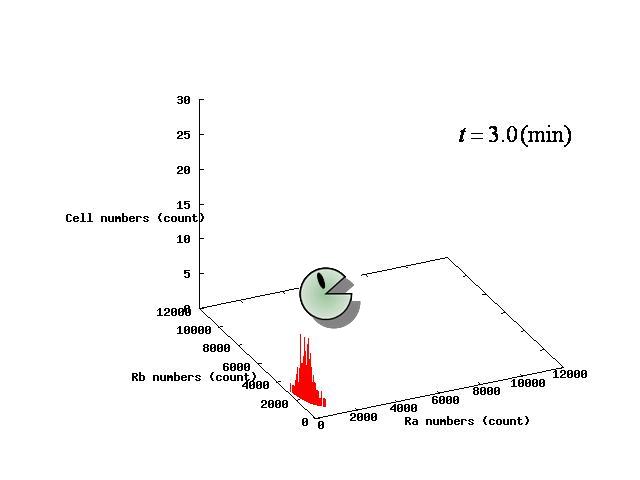
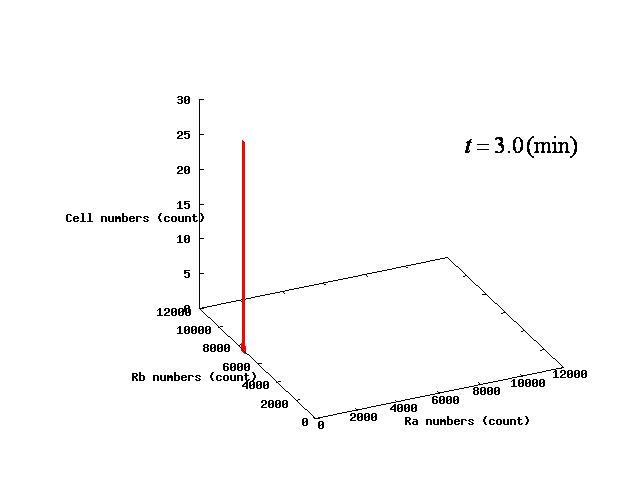
Multi-cell simulations with Hill coefficients of the promoters were carried out to find ranges of other parameters that lead the system to balanced differentiation. The differential equations for N cells were constructed to describe the cell population interacting with each other(Ex3.1). | Multi-cell simulations with Hill coefficients of the promoters were carried out to find ranges of other parameters that lead the system to balanced differentiation. The differential equations for N cells were constructed to describe the cell population interacting with each other(Ex3.1). | ||
| - | ''' | + | |
| + | '''HEREの段落をグラフの右に書きたいですが簡単?''' | ||
| + | Here, the concentration of AHL outside of the cells was assumed to be the same concentration of AHL inside the cell because AHL is freely permeable through the membrane of each cell [引用文献番号]. First, the phase plane analysis for the equations was carried out by focusing on an individual cell. | ||
| Line 13: | Line 15: | ||
<br>[[Image:expression5-1.jpg|400px|thumb|none|Ex3.2 the stochastic differential equations of the population model]] | <br>[[Image:expression5-1.jpg|400px|thumb|none|Ex3.2 the stochastic differential equations of the population model]] | ||
| - | + | In the simulations, Hill coefficients, coefficients of repression and activation of AHL and LacI(n2,n3,k2,k3) determined by the wet experiments were used. | |
| - | + | ||
| - | <br> | + | <br>n2 = 2.08 (-) |
| - | <br> | + | <br>K2 = 4.05 (μM) |
| - | <br> | + | <br>n3 = 2.47 (-) |
| - | <br> | + | <br>K3 = 0.295 (μM) |
==<!--共存安定になるようなパラメータ範囲の提示-->Determining the range of parameter which satisfy coexistent stability== | ==<!--共存安定になるようなパラメータ範囲の提示-->Determining the range of parameter which satisfy coexistent stability== | ||
| - | ===The example of coexistent stable | + | <!--===The example of coexistent stable state共存安定状態の例=== --> |
| + | Depending on the value of parameter λ, three different patterns were observed: the pattern with coexistence state of A and B states, the pattern with only A state, and the pattern with only B. The simulation results for their patterns are shown in Fig.1 to 3. | ||
| + | |||
<!--パラメータλの値によって,AとBが共存して安定する場合と,Aのみ,Bのみになってしまう3つのパターンが生じる. | <!--パラメータλの値によって,AとBが共存して安定する場合と,Aのみ,Bのみになってしまう3つのパターンが生じる. | ||
それぞれのパターンについてシミュレーション結果を示すとFig.1-3のようになる.--> | それぞれのパターンについてシミュレーション結果を示すとFig.1-3のようになる.--> | ||
| Line 49: | Line 52: | ||
<br> | <br> | ||
<!--3パターンについて,nullclinesの交点が2つになる瞬間の相平面はFig.4.A-Cのようになる.--> | <!--3パターンについて,nullclinesの交点が2つになる瞬間の相平面はFig.4.A-Cのようになる.--> | ||
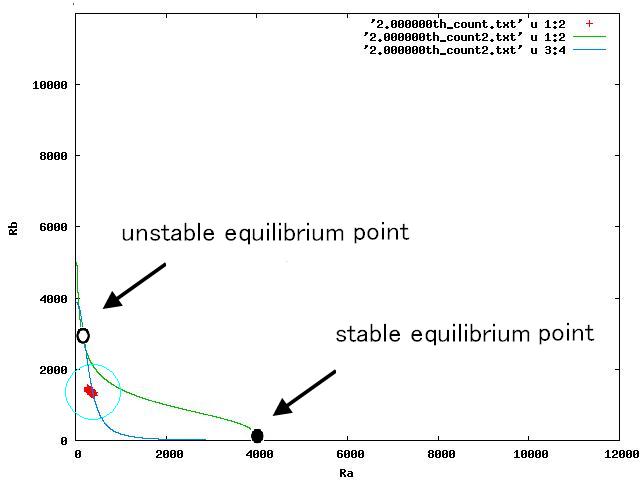
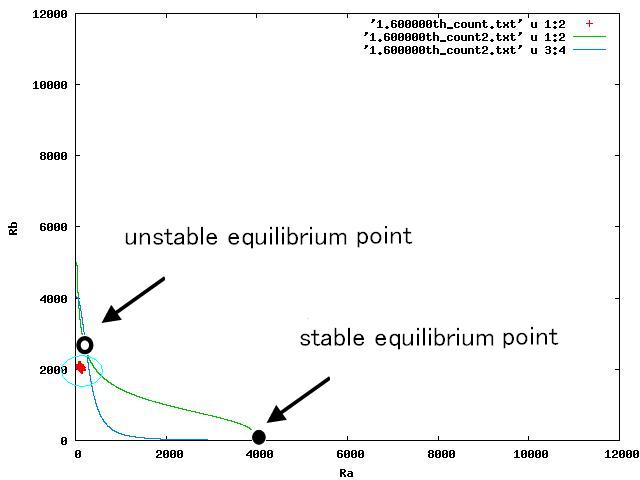
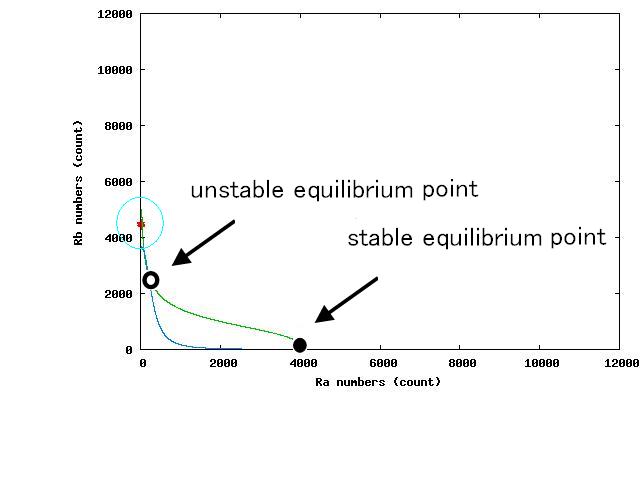
| - | + | The nullclines changed dependent on the state of the cell population. When there are only B cells, the nullclines had one intersection in the phase plane. As change of the state of the cell population, the number of the intersections of nullclines turned into two. Fig.4.A-C shows the appearance of an additional intersection, indicating an unstable equilibrium point, for the three patterns, respectively. | |
<!--相平面:phase portrait | <!--相平面:phase portrait | ||
nullclinesの交点:the intersection of the nullclines--> | nullclinesの交点:the intersection of the nullclines--> | ||
| Line 55: | Line 58: | ||
[[Image:2Dpp-ab-tt.JPG|260px|left|thumb|Fig.4.B]] | [[Image:2Dpp-ab-tt.JPG|260px|left|thumb|Fig.4.B]] | ||
[[Image:2Dpp-b-tt.JPG|260px|none|thumb|Fig.4.C]] | [[Image:2Dpp-b-tt.JPG|260px|none|thumb|Fig.4.C]] | ||
| - | <br>Fig. | + | |
| + | <br>In the case of Fig. 4B, the cell population distributed around the unstable equilibrium point. Right after the moment shown in the Fig. 4B, some cells moved to the A state and the other go in the direction of the B state. The division of the direction may have occurred due to the distribution of the population over the both sides of a “watershed” which is a division line lying over the unstable equilibrium point. In another possibility, fluctuation of the cell state might allow coming or going over the division line. | ||
<!--Fig.4.Aでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりA側に存在している.逆に,Fig.4.Cでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりもB側に存在している. | <!--Fig.4.Aでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりA側に存在している.逆に,Fig.4.Cでは,平衡点が二つになった瞬間,cellsは中心付近の不安定平衡点よりもB側に存在している. | ||
| Line 66: | Line 70: | ||
===[[Tokyo/Works/Simulation/B phase plane movie| ⇒ movie about Fig.4.C here!!]]=== | ===[[Tokyo/Works/Simulation/B phase plane movie| ⇒ movie about Fig.4.C here!!]]=== | ||
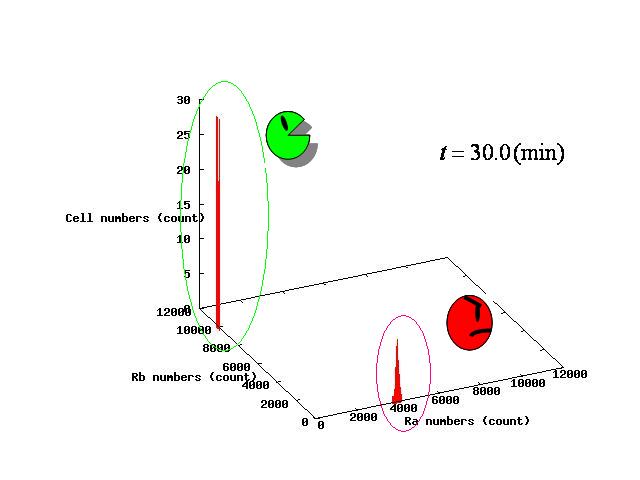
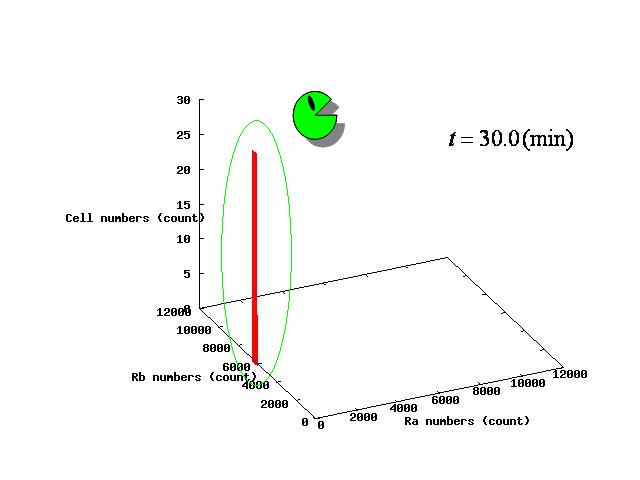
| - | + | In the case of Fig. 4A, all the cells existed on the A-side rather than the B-side compared to the dividing line. Therefore, all the cells was not able to cross over the dividing line and moved to the A state. In contrast, when all the cells existed on the B-side rather than the A-side ( Fig 4.C), all the cells moved to the B state, similarly. | |
===The range of parameter λ <!--範囲の提示-->=== | ===The range of parameter λ <!--範囲の提示-->=== | ||
| - | <!--共存安定になるパラメータλの範囲を調べるため,λを変化させてシミュレーションをした.その結果,λの値とAとBが共存安定する確率の関係はFig.5のようになった.-->To determine the range of parameter λ, | + | <!--共存安定になるパラメータλの範囲を調べるため,λを変化させてシミュレーションをした.その結果,λの値とAとBが共存安定する確率の関係はFig.5のようになった.--> |
| + | |||
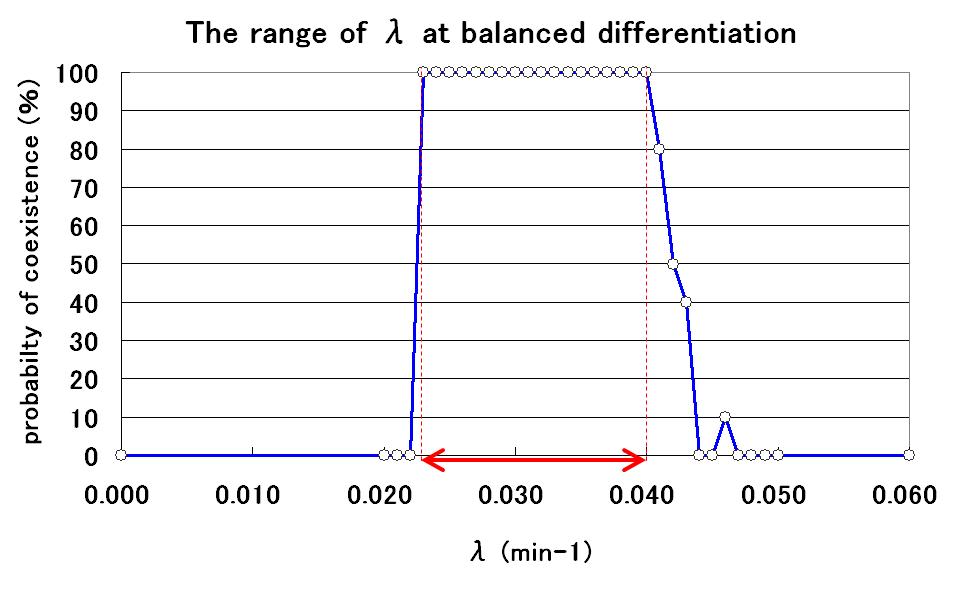
| + | To determine the range of the value of parameter λ for balanced differentiation, further simulations were carried out by changing the value of λ. As a result, the relationship between the value of λ and the probability of balanced differentiation was determined as shown in Fig.5. | ||
| + | |||
[[Image:range_of_lambda.JPG|400px|thumb|none|Fig.5]] | [[Image:range_of_lambda.JPG|400px|thumb|none|Fig.5]] | ||
<!--よって,パラメータλをこの範囲の中に入るように調節すれば,我々が目的としているモデルを作り出すことができる!--> | <!--よって,パラメータλをこの範囲の中に入るように調節すれば,我々が目的としているモデルを作り出すことができる!--> | ||
| - | '''By using parameter λ in this range, we can construct | + | '''By using parameter λ in this range, we can construct the artificial genetic circuit for balanced differentiation!''' |
<!--[[Image:Parameter set before.JPG]]--> | <!--[[Image:Parameter set before.JPG]]--> | ||
Revision as of 18:07, 26 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
Multi-cell simulations with Hill coefficients of the promoters were carried out to find ranges of other parameters that lead the system to balanced differentiation. The differential equations for N cells were constructed to describe the cell population interacting with each other(Ex3.1).
HEREの段落をグラフの右に書きたいですが簡単? Here, the concentration of AHL outside of the cells was assumed to be the same concentration of AHL inside the cell because AHL is freely permeable through the membrane of each cell [引用文献番号]. First, the phase plane analysis for the equations was carried out by focusing on an individual cell.
To analyze the behavior of the cell population, the above differential equations for N cells were extended to the stochastic differential equations(Ex3.2). In order to carry out the simulations with the stochastic model, Poisson random variables were introduced into the differential equations. As a result of the stochastic simulation, the different behaviors of individual cells were observed.
In the simulations, Hill coefficients, coefficients of repression and activation of AHL and LacI(n2,n3,k2,k3) determined by the wet experiments were used.
n2 = 2.08 (-)
K2 = 4.05 (μM)
n3 = 2.47 (-)
K3 = 0.295 (μM)
Determining the range of parameter which satisfy coexistent stability
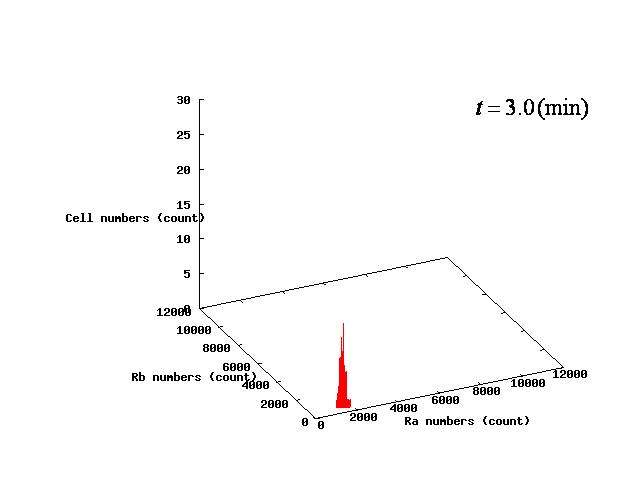
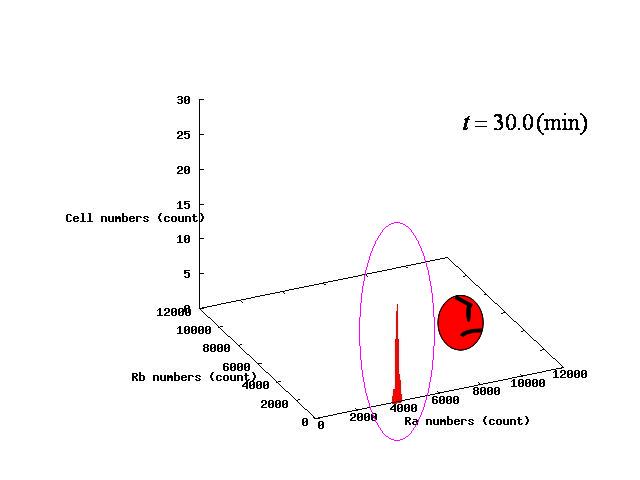
Depending on the value of parameter λ, three different patterns were observed: the pattern with coexistence state of A and B states, the pattern with only A state, and the pattern with only B. The simulation results for their patterns are shown in Fig.1 to 3.
⇒ movie here!!
⇒ movie here!!
⇒ movie here!!
The nullclines changed dependent on the state of the cell population. When there are only B cells, the nullclines had one intersection in the phase plane. As change of the state of the cell population, the number of the intersections of nullclines turned into two. Fig.4.A-C shows the appearance of an additional intersection, indicating an unstable equilibrium point, for the three patterns, respectively.
In the case of Fig. 4B, the cell population distributed around the unstable equilibrium point. Right after the moment shown in the Fig. 4B, some cells moved to the A state and the other go in the direction of the B state. The division of the direction may have occurred due to the distribution of the population over the both sides of a “watershed” which is a division line lying over the unstable equilibrium point. In another possibility, fluctuation of the cell state might allow coming or going over the division line.
⇒ movie about Fig.4.A here!!
⇒ movie about Fig.4.B here!!
⇒ movie about Fig.4.C here!!
In the case of Fig. 4A, all the cells existed on the A-side rather than the B-side compared to the dividing line. Therefore, all the cells was not able to cross over the dividing line and moved to the A state. In contrast, when all the cells existed on the B-side rather than the A-side ( Fig 4.C), all the cells moved to the B state, similarly.
The range of parameter λ
To determine the range of the value of parameter λ for balanced differentiation, further simulations were carried out by changing the value of λ. As a result, the relationship between the value of λ and the probability of balanced differentiation was determined as shown in Fig.5.
By using parameter λ in this range, we can construct the artificial genetic circuit for balanced differentiation!