Paris/Cell auto
From 2007.igem.org
(→Dynamics) |
|||
| (40 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Template:Paris_menu_modeling}} | {{Template:Paris_menu_modeling}} | ||
| + | |||
<br> | <br> | ||
| + | |||
| + | In this part of our work, we aim at characterizing the diffusion of the DAP and the effect on the cells differentiation. This study consists in observing by simulation, the diffusion of DAP in a lawn of germ cells with some isolated somatic cells using a cellular automaton. | ||
| + | |||
<br> | <br> | ||
| - | |||
| - | |||
| - | = | + | = Introduction = |
| - | + | DAP feeding between somatic and germ cells is based on an indirect communication process: soma cells produce DAP and release it in the environment; DAP molecules freely diffuse outside until they are captured by a germ cell. As the diffusion takes place in the environment, a somatic cell feed first the germ cells that are close to it. Then an well mixed hypothesis as the one used in the our [[Paris/Continuous_model|growth of population analysis]] is hard to assume. We are interesting here in the case where the differentiation of a germ into a soma is DAP dependent. In order to figure out the relation between DAP diffusion and differentiation we propose a simple cellular automaton on square grid. Each cell of the automaton contains a bacterium. We first detail some hypotheses used in this model, then we specify the local behavior rules following by each automaton cell. Finally, the generated simulation is presented. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | = Hypotheses = |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | The chosen approach consists in observing the DAP diffusion and differentiation frontwaves. In order to focus on these phenomenon, we work on a ''constant'' population (no death, no division). So we assume that without DAP in its surrounding, a germ cell does not die but remain in passive state (we can imagine that they are at a stationary phase or between to division cycle). It will seem that DAP ''wake up'' bacteria but it's just an artifact due to this assumption. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ''' | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ==''''' | + | It may happen that a germ cell as enough DAP to evolve (typically when it is touched by a DAP diffusion front) but we assume that the contribution is not enough for the cell to divide. |
| - | < | + | |
| - | The output is two animated pictures one | + | Finally, we assume then that DAP is produced in somatic cells only and consumed by germ cells. The communication is done by distinguishing in the automaton intra and extra cellular DAP (respectively named DAPi and DAPe). |
| + | |||
| + | = Model Description = | ||
| + | |||
| + | In this we focus on the elaboration of the cellular automaton. | ||
| + | |||
| + | == Structure == | ||
| + | |||
| + | As we have previously announced, we design cellular automaton on a square grid. More precisely, in order to avoid boundary effects, we assume that the grid is actually wrapped in such a way the grid topology is a 2D torus. Each cell of the automaton contains a bacterium, either germ or somatic, together with the external DAP concentration. So we represent the different states of the automaton cell by tuple of values <code>{DAPe,DAPi,Type}</code>: | ||
| + | |||
| + | * <code>DAPe</code> is the external DAP concentration, | ||
| + | |||
| + | * <code>DAPi</code> is the internal DAP concentration in the bacterium, | ||
| + | |||
| + | * <code>Type</code> represents if the bacterium is differentiated or not; it can take two values <code>BactG</code> and <code>BactS</code>. | ||
| + | |||
| + | == Dynamics == | ||
| + | |||
| + | The following rules specify the local evolution of each cell of the automaton. We distinguished to evolution laws depending on what kind of bacterium is in the cell: | ||
| + | |||
| + | *<html><u>In the case of a somatic cell</u></html>: we have to consider the diffusion of <code>DAPe</code> between the considered cell and its neighbors, the export of DAP from the inside to the outside, and finally the production of <code>DAPi</code>. The rule can be presented as follows: | ||
| + | |||
| + | DAPe <- DAPe + (DAPe diffused in the neighborhood) + (DAPi lost by export) | ||
| + | DAPi <- DAPi + (DAPi produced) - (DAPi lost by export) | ||
| + | Type <- BactS | ||
| + | |||
| + | *<html><u>In the case of a germ cell</u></html>: we have to consider the diffusion of <code>DAPe</code> between the considered cell and its neighbors, the import of DAP from the outside to the inside, the consumption of <code>DAPi</code>, and finally the differentiation when DAP concentration reaches a right range of values. The rule can be presented as follows: | ||
| + | |||
| + | DAPe <- DAPe + (DAPe diffused in the neighborhood) - (DAPi gain by import) | ||
| + | DAPi <- DAPi - (DAPi consumed) + (DAPi gain by import) | ||
| + | Type <- '''if''' (min_threshold) < DAPi < (max_threshold) '''then''' BactS '''else''' BactG | ||
| + | |||
| + | == Parameters == | ||
| + | |||
| + | We consider 8 parameters. They are used with some noise during the evolution to avoid a deterministic behavior. | ||
| + | |||
| + | * In <code>BactS</code> cells: | ||
| + | |||
| + | :* Dap export rate in somatic bacteria | ||
| + | |||
| + | :* Dap import rate in somatic bacteria | ||
| + | |||
| + | :* Dap production rate of somatic bacteria | ||
| + | |||
| + | * In <code>BactG</code> cells: | ||
| + | |||
| + | :* Dap export rate in germ bacteria | ||
| + | |||
| + | :* Dap import rate in germ bacteria | ||
| + | |||
| + | :* Dap consummation rate of germ bacteria | ||
| + | |||
| + | :* Minimal threshold for differentiation | ||
| + | |||
| + | :* Maximal threshold for differentiation | ||
| + | |||
| + | == Initial state == | ||
| + | |||
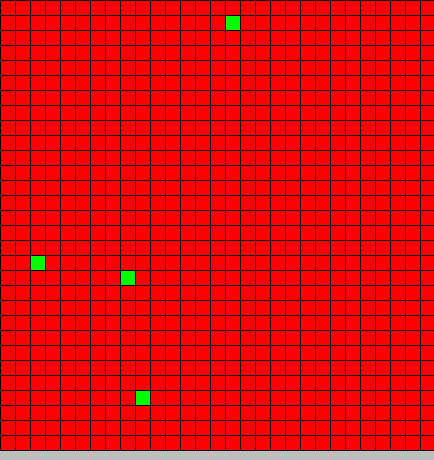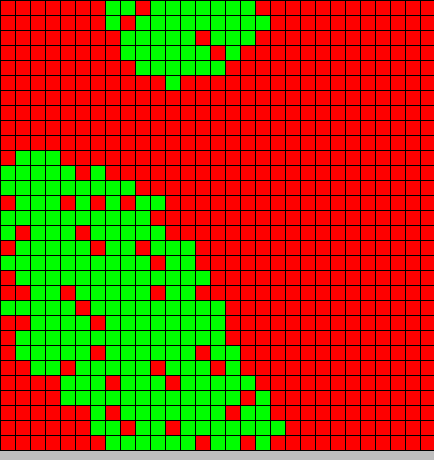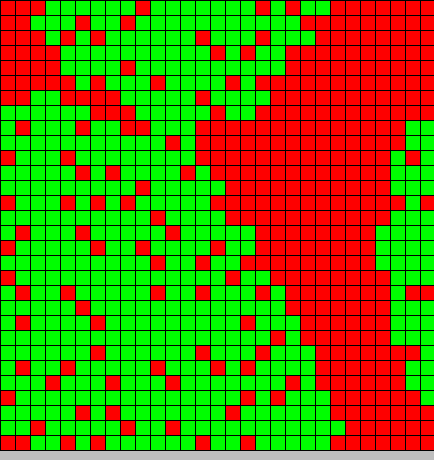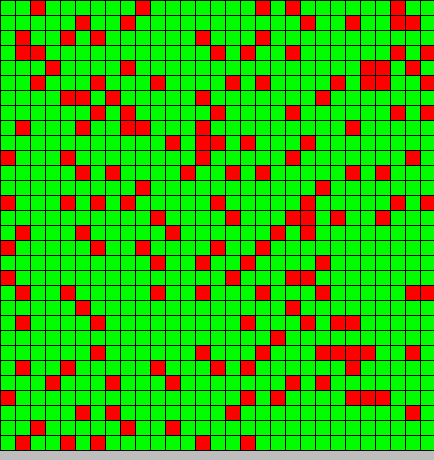
| + | Our initial state is 30x30 2D toric cellular automaton where all cells are initialized by value <code>{DAPe=0,DAPi=0,Type=BactG}</code> but four <code>{DAPe=0,DAPi=0,Type=BactS}</code> are randomly placed in the grid. | ||
| + | |||
| + | |||
| + | |||
| + | = Output [[Image:MGS-inside.png|50px]]= | ||
| + | |||
| + | Our implementation was done in [[Paris/mgs|MGS]] and the output was generated by [http://www.sciences.univ-nantes.fr/info/perso/permanents/cohen/SOFTWARE/GBVIEW/index.html GBView]. | ||
| + | |||
| + | The output is two animated pictures: the first one shows the differentiation, the other the diffusion of DAPe<br> | ||
<center>[[Image:Paris\Diff_DAP.gif|Dap diffusion]][[Image:Paris\Diffe.gif|Bact differentiation]]</center><br> | <center>[[Image:Paris\Diff_DAP.gif|Dap diffusion]][[Image:Paris\Diffe.gif|Bact differentiation]]</center><br> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | *The first picture shows the diffusion of DAP: the front wave is figured in light blue; the dark blue area corresponds to stable parts of the system where concentration do not evolve anymore. | |
| - | *The | + | |
| - | + | *The second picture presents the differentiation: red and blue cells are respectively germ and somatic bacteria. | |
| - | + | ||
| - | + | = Results = | |
| - | : | + | |
| + | As we can see, the differentiation and DAP diffusion wave fronts are superposed. This simulation is obviously out of reality but the underlying model have been developed in order to consider that low concentration of DAP induces differentiation (cells become green - dark blue), while with high DAP concentration, the differentiation is inhibited. Without this second threshold, all cells would differentiate. But some germ cells remain because they are enough fed to stay over the threshold. This property is of course crucial as only germ cells can reproduce. | ||
| + | |||
| + | In the considered model of the system, the inhibition must be strong and effective for not all the cells differentiate. Bad thresholds make the system collapse: a too strong inhibition prevents germ cells to differentiate, and on the opposite, a too weak inhibition make all them switch to a somatic state. | ||
| + | |||
| + | By tuning the constant of diffusion, we have noted that the 3 steps communication process (export, diffusion, import) is of main interest. For a few molecules of DAP imported in germ cells, an important amount of produced DAP has to be produced: there is a lot of lost during the process. So in order to keep a coherent rate of production, a germ cell must be surrounded by a lot of somatic bacteria: the ratio of 1:1 of differentiated and germ cell is not viable, that is why a lot of somatic cells feed isolated germ bacteria as enlighten by the animations. | ||
| + | |||
| + | = [[Paris\Sources#Cell auto|Sources]] = | ||
Latest revision as of 21:27, 26 October 2007
In this part of our work, we aim at characterizing the diffusion of the DAP and the effect on the cells differentiation. This study consists in observing by simulation, the diffusion of DAP in a lawn of germ cells with some isolated somatic cells using a cellular automaton.
Contents |
Introduction
DAP feeding between somatic and germ cells is based on an indirect communication process: soma cells produce DAP and release it in the environment; DAP molecules freely diffuse outside until they are captured by a germ cell. As the diffusion takes place in the environment, a somatic cell feed first the germ cells that are close to it. Then an well mixed hypothesis as the one used in the our growth of population analysis is hard to assume. We are interesting here in the case where the differentiation of a germ into a soma is DAP dependent. In order to figure out the relation between DAP diffusion and differentiation we propose a simple cellular automaton on square grid. Each cell of the automaton contains a bacterium. We first detail some hypotheses used in this model, then we specify the local behavior rules following by each automaton cell. Finally, the generated simulation is presented.
Hypotheses
The chosen approach consists in observing the DAP diffusion and differentiation frontwaves. In order to focus on these phenomenon, we work on a constant population (no death, no division). So we assume that without DAP in its surrounding, a germ cell does not die but remain in passive state (we can imagine that they are at a stationary phase or between to division cycle). It will seem that DAP wake up bacteria but it's just an artifact due to this assumption.
It may happen that a germ cell as enough DAP to evolve (typically when it is touched by a DAP diffusion front) but we assume that the contribution is not enough for the cell to divide.
Finally, we assume then that DAP is produced in somatic cells only and consumed by germ cells. The communication is done by distinguishing in the automaton intra and extra cellular DAP (respectively named DAPi and DAPe).
Model Description
In this we focus on the elaboration of the cellular automaton.
Structure
As we have previously announced, we design cellular automaton on a square grid. More precisely, in order to avoid boundary effects, we assume that the grid is actually wrapped in such a way the grid topology is a 2D torus. Each cell of the automaton contains a bacterium, either germ or somatic, together with the external DAP concentration. So we represent the different states of the automaton cell by tuple of values {DAPe,DAPi,Type}:
-
DAPeis the external DAP concentration,
-
DAPiis the internal DAP concentration in the bacterium,
-
Typerepresents if the bacterium is differentiated or not; it can take two valuesBactGandBactS.
Dynamics
The following rules specify the local evolution of each cell of the automaton. We distinguished to evolution laws depending on what kind of bacterium is in the cell:
- In the case of a somatic cell: we have to consider the diffusion of
DAPebetween the considered cell and its neighbors, the export of DAP from the inside to the outside, and finally the production ofDAPi. The rule can be presented as follows:
DAPe <- DAPe + (DAPe diffused in the neighborhood) + (DAPi lost by export) DAPi <- DAPi + (DAPi produced) - (DAPi lost by export) Type <- BactS
- In the case of a germ cell: we have to consider the diffusion of
DAPebetween the considered cell and its neighbors, the import of DAP from the outside to the inside, the consumption ofDAPi, and finally the differentiation when DAP concentration reaches a right range of values. The rule can be presented as follows:
DAPe <- DAPe + (DAPe diffused in the neighborhood) - (DAPi gain by import) DAPi <- DAPi - (DAPi consumed) + (DAPi gain by import) Type <- if (min_threshold) < DAPi < (max_threshold) then BactS else BactG
Parameters
We consider 8 parameters. They are used with some noise during the evolution to avoid a deterministic behavior.
- In
BactScells:
- Dap export rate in somatic bacteria
- Dap import rate in somatic bacteria
- Dap production rate of somatic bacteria
- In
BactGcells:
- Dap export rate in germ bacteria
- Dap import rate in germ bacteria
- Dap consummation rate of germ bacteria
- Minimal threshold for differentiation
- Maximal threshold for differentiation
Initial state
Our initial state is 30x30 2D toric cellular automaton where all cells are initialized by value {DAPe=0,DAPi=0,Type=BactG} but four {DAPe=0,DAPi=0,Type=BactS} are randomly placed in the grid.
Output 
Our implementation was done in MGS and the output was generated by [http://www.sciences.univ-nantes.fr/info/perso/permanents/cohen/SOFTWARE/GBVIEW/index.html GBView].
The output is two animated pictures: the first one shows the differentiation, the other the diffusion of DAPe

- The first picture shows the diffusion of DAP: the front wave is figured in light blue; the dark blue area corresponds to stable parts of the system where concentration do not evolve anymore.
- The second picture presents the differentiation: red and blue cells are respectively germ and somatic bacteria.
Results
As we can see, the differentiation and DAP diffusion wave fronts are superposed. This simulation is obviously out of reality but the underlying model have been developed in order to consider that low concentration of DAP induces differentiation (cells become green - dark blue), while with high DAP concentration, the differentiation is inhibited. Without this second threshold, all cells would differentiate. But some germ cells remain because they are enough fed to stay over the threshold. This property is of course crucial as only germ cells can reproduce.
In the considered model of the system, the inhibition must be strong and effective for not all the cells differentiate. Bad thresholds make the system collapse: a too strong inhibition prevents germ cells to differentiate, and on the opposite, a too weak inhibition make all them switch to a somatic state.
By tuning the constant of diffusion, we have noted that the 3 steps communication process (export, diffusion, import) is of main interest. For a few molecules of DAP imported in germ cells, an important amount of produced DAP has to be produced: there is a lot of lost during the process. So in order to keep a coherent rate of production, a germ cell must be surrounded by a lot of somatic bacteria: the ratio of 1:1 of differentiated and germ cell is not viable, that is why a lot of somatic cells feed isolated germ bacteria as enlighten by the animations.
