Tokyo/Model
From 2007.igem.org
(Difference between revisions)
(/* To establish a system following Pareto’s principle(for example Ant society), the system must satisfy the following three cases. In our model, all nodes have the same genetic circuits and take two states, A (worker) and B (idler), d) |
|||
| Line 11: | Line 11: | ||
[[Image:model2.jpg]] | [[Image:model2.jpg]] | ||
| - | <br> | + | <br>By removal of node A, the system contains only node B and becomes unstable. <--Node B detects the removal of node A from the system and knows that there is only node B left.--> |
'''Condition 3. From unstable to stable state''' | '''Condition 3. From unstable to stable state''' | ||
[[Image:model3.jpg]] | [[Image:model3.jpg]] | ||
| - | <br>In | + | <br>In the unstable state, some node B become A while the others remain B. The system then becomes stable again. |
[[Image:concepts.jpg]] | [[Image:concepts.jpg]] | ||
Revision as of 11:17, 23 October 2007
Abstruct Concept & Model Requirements Genetic_circuit Works About_our_team
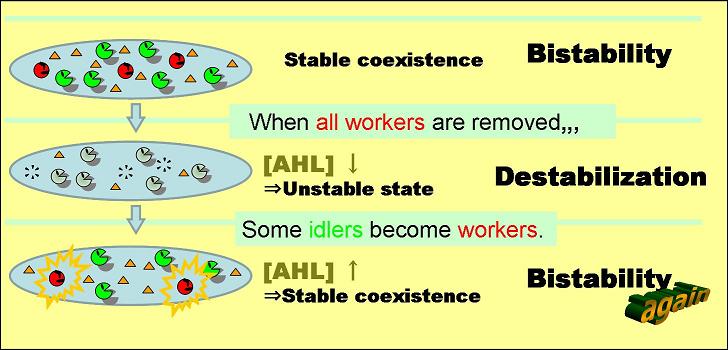
To establish a system following Pareto’s principle(for example Ant society), the system must satisfy the following three cases. In our model, all nodes have the same genetic circuits and take two states, A (worker) and B (idler), depending on the surrounding circumstances.
Condition 1. Bistable state

The system is stable containing nodes A and B at certain ratio.
Condition 2. Unstable state with node A removed

By removal of node A, the system contains only node B and becomes unstable. <--Node B detects the removal of node A from the system and knows that there is only node B left.-->
Condition 3. From unstable to stable state
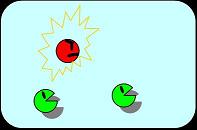
In the unstable state, some node B become A while the others remain B. The system then becomes stable again.