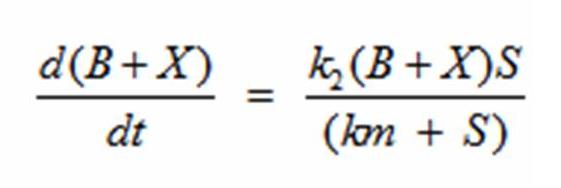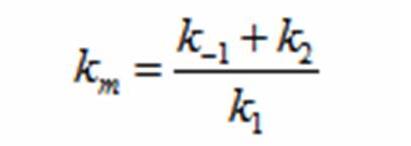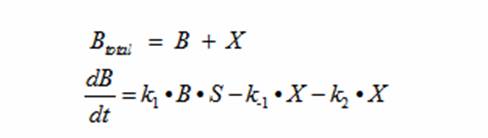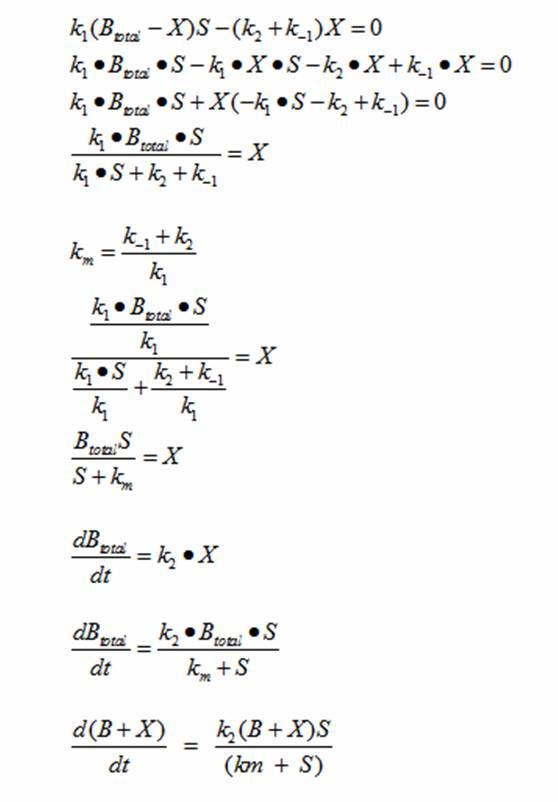Virginia Tech/bacteria model
From 2007.igem.org
| Line 220: | Line 220: | ||
At steady state: | At steady state: | ||
[[Image:SteadyState.jpg|thumb|left|300px]] | [[Image:SteadyState.jpg|thumb|left|300px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | This equation models the growth of bacteria; however, a second differential equation is needed to show the decline of the food substrate as the bacteria consumes it. The substrate S stays constant so there is unlimited food. dS/dt must be derived to create a sigmoid curve. | ||
|}<html></center></html> | |}<html></center></html> | ||
Revision as of 03:06, 24 October 2007
|
|
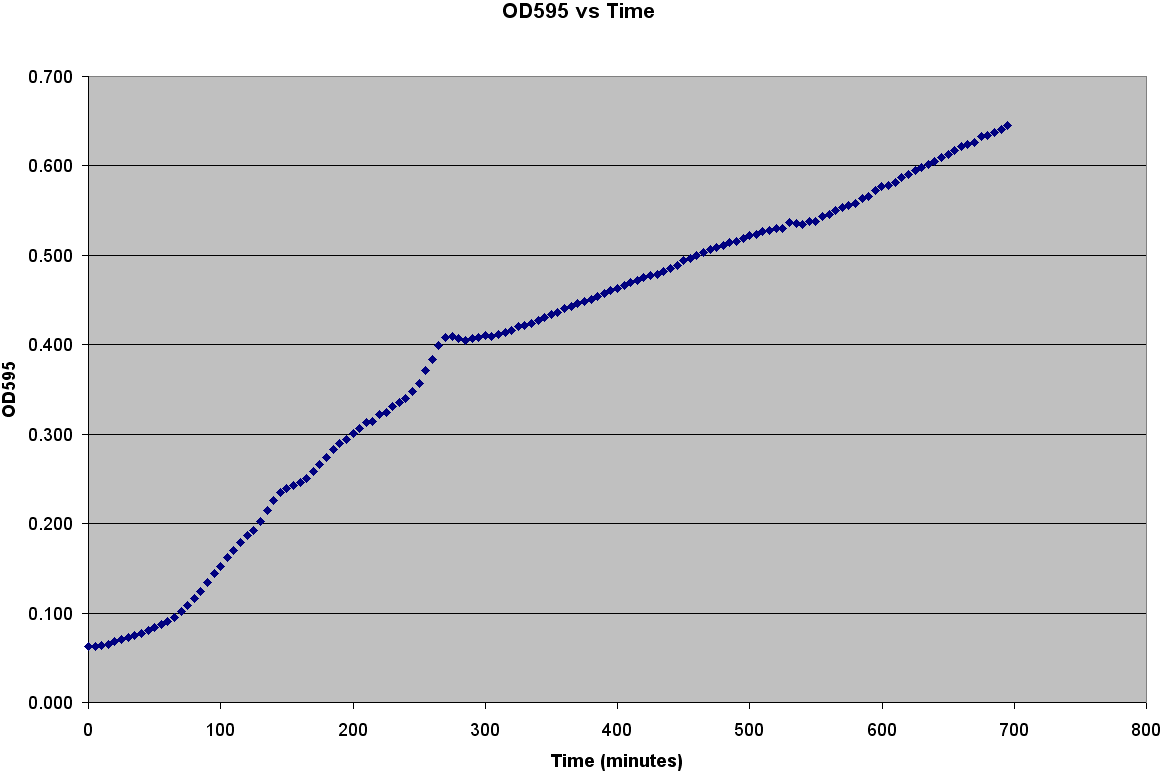
The first step to modeling the spread of an epidemic is to model the population itself.If you do not understand how the population grows, then how is it possible to understand the spread of a disease through that population? It is very easy to grow E. coli; it only needs some media, a warm environment, and some aeration. The problem is generating the growth curve. It is possible to measure the OD600 over a period of time, but the team wanted to generate data with number of bacteria. Collecting Experimental DataGenerating the Calibration CurveThe team decided to generate OD600 vs Time, OD600 vs CFU/mL, and CFU/mL vs Time curves. It was also decided to grow two different strains of bacteria C600 and LE392 in both LB and TNT media. This was accomplished using the following procedure: ATCC C600 and LE392 were regenerated from a previous overnight culture. These cultures were used to inoculate four Corning Tubes labeled: "LE392 in TNT," "LE392 in LB," "C600 in TNT," and "C600 in LB." (These were the four different growth curves generated). Each culture was allowed to grow for at 37oC and 220 rpm. Aliquots were taken every 30 minutes starting at T=0. An OD600 was taken from each of these aliquots. Serial dilutions were made of each aliquot and they were then plated to grow overnight. This was done for a total of four hours. The plates provided us with colony forming units per mL (CFU/mL), which could then be graphed against OD600. This provided the calibration curve necessary to determine number of cells per well. Measuring Bacterial GrowthAfter producing a calibration curve to convert OD600 measurements to total number of cells, we decided to use the new plate reader to measure growth of LE392 in a single well. The new plate reader allows for temperature control, shaking, and can take numerous readings very quickly. Thus, we could follow the growth of LE392 in 96 wells without a considerable amount of work. The only problem was the small volume in each well made it easy for evaporation to occur, but this was compensated for by adding sterilized MilliQ water part of the way through the experiment.
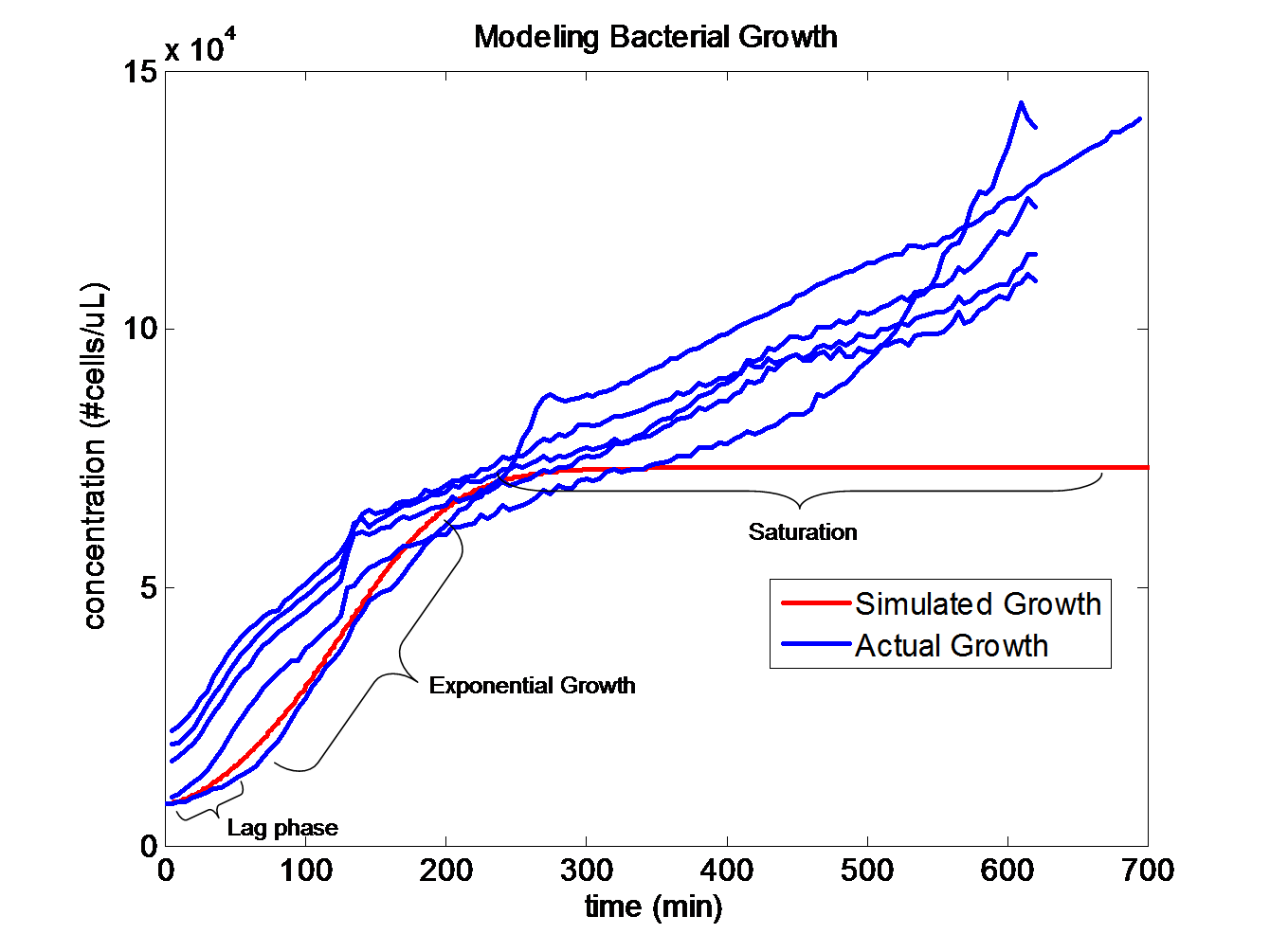
Simulating Bacterial GrowthPopulation growth curves tend to have a sigmoid growth trajectory. In order to create a sigmoid growth curve, we start with Michaelis Menten's model that describes enzyme kinetics with a limiting substrate. The Michaelis Menten reaction equation is
In terms of B(bacteria), X(intermediate), and S(substrate), the Monad equation can be written as
The rate k2 controls the exponential growth and the rate km controls the peak of the curve.
DerivationsMonad’s equation can be directly derived from the reaction equation
The derivation for Monad’s equation:
|