From 2007.igem.org

Revision as of 16:06, 21 October 2007

Test

Introduction

As it has been already discussed in the main page, we are interested in designing a system that is able to adapt to its environment. Our ideas were based on discussions about neural networks, and on how we can create a biological system that exhibits the behavior of learning, without having to resort to evolutionary processes.

Fig. 1: Flow diagram. This figure shows the protocol with which the final system should be tested as well as the test results in form of the reported colors. There are tree phases the systems has to perform: (1) a training or learning phase in which the system learns an input and stores it in its memory, (2) a memory phase in which the system has to keep the content of its memory and finally (3) a recognition phase where the output of the system depends on the content of its memory as well as on the current input.

Learning can be considered as a switching of behavior, based on some external stimuli. It comes thus naturally, to work on existing ideas of toggle switches and finite state automatons.

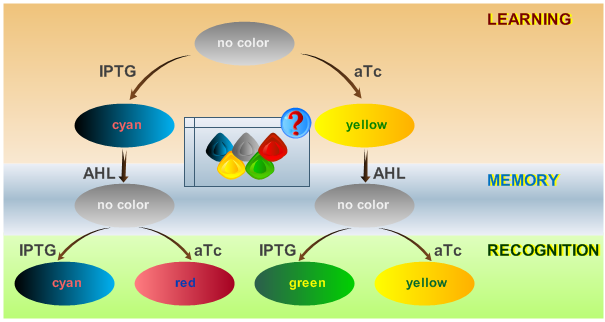
In our system, we are able to distinguish only between two chemicals. The proposed is only a minimal system that should be able to act as a proof of concept. By introducing the ability to have more final states, in an abstract manner, this correlates with the level of "intelligence" of the biological system. A protocol on how the system should react according to an input is shown in Fig. 1.

The idea behind this protocol is that:

• The system will be able to learn one of two input signals - aTc or IPTG - during a learning phase if no input signal AHL is present. Depending on the input it will report by producing either green or yellow florescence.
• Once the system has learned, the inputs - aTc or IPTG - can be removed and the system goes into a memory state in the presence of the "helper" substance AHL. In this state no output color is reported. Memorizing is guaranteed by removing the input chemicals. This results in a following successful recognition phase.
• During the recognition phase, the inputs aTc or IPTG are (re-)inserted. The system reports by changing its color depending on the input and its current memory state. This is why the system has different florescent properties even in the presence of the same input. The recognition phase takes place in the presence of AHL to keep the memory enabled and avoid another learning phase. Since we would like to separate four different end states for our system, we had to use four fluorescent proteins to encode them.

Model Overview

One can start developing our system with a top-down approach. We start with the classical back box approach as shown in Figure 2.

Fig. 2: Black box

Based on what was discussed in the previous section, the properties that our system has can be summarized as follows:

• We need two inputs that should be learned/detected/adapted to,
• We need one input to switch on the memory.
• We need to alternate between at least three states. That is why we decided to use two state variables - cI and p22cII.
• We need four florescent signals for the outputs. One could also decide to take six output signals into account, to further distinguish the learning phase from the recognition phase. However, we restricted ourselves to 4 outputs to reduce the number of genes that are needed to implement the signals.

Fig. 3: System overview. AHL, IPTG and aTc are passing the cell membrane where they build complexes with the sensor proteins LuxR, LacI and TetR. These sensor proteins and/or complexes are used to control memory formation and the production of the reporter proteins. The memory content is represented by the proteins cI and p22cII that repress the production of each other. YFP, RFP, CFP and GFP stand for yellow, red, cyan and green florescent protein, respectively.

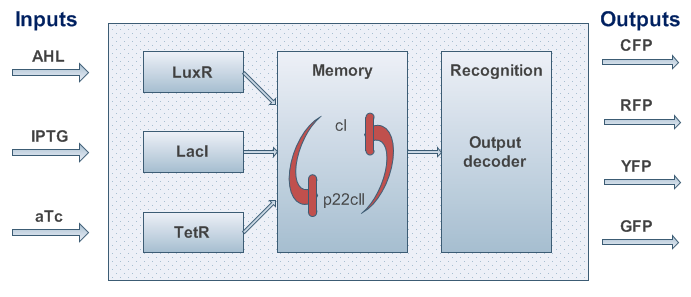
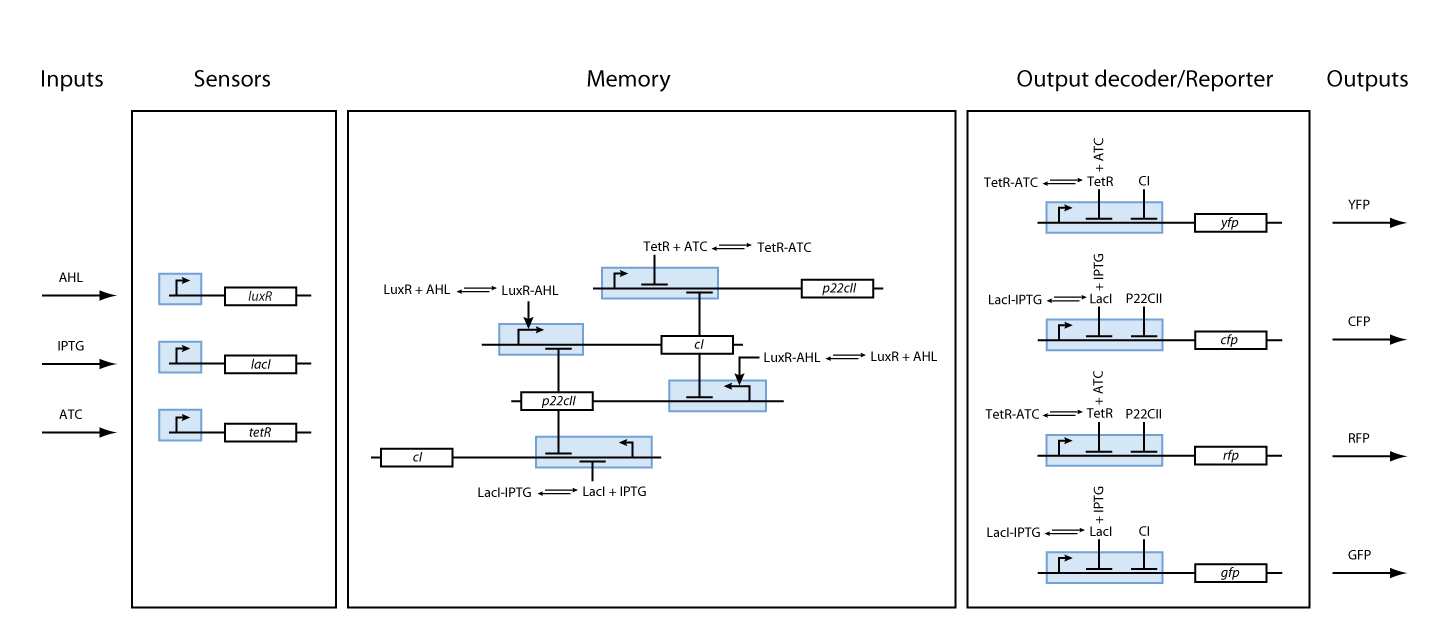
Based on the above, the internal structure of the system can be defined, and it can be seen in Figure 3. However, we had to keep in mind that the proposed system should be implemented in DNA, and that it would be sensitive to noise. As a result, we took several actions to achieve better experimental results and easier DNA construction:

• To be more robust against perturbations, we coupled the state variables cI and p22cII in the way that is well known from memory circuits. Based on this approach, one state variable is depressing the other one, and the system's internal toggle has the possibility of reaching two stable states.
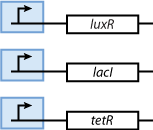
• Since - due to their size - proteins can only hardly pass the cell membrane (if they are not actively transported through the cell membrane), we decided to use the much smaller inducer molecules AHL, IPTG and aTc as inputs. However, since these inducers cannot directly act on the transcription of the DNA nor on the production of proteins, we need to produce the sensor proteins LuxR, LacI and TetR that build complexes with AHL, IPTG and aTc, respectively.
• The sensor proteins and complexes are used to control the memory formation and the production of the florescent reporter proteins YFP, RFP, CFP and GFP.
  
  

Detailed Model

In order to test our ideas, we had to find the equations that describe the proposed model, and fill in the gaps. In this section, we are providing the details of our model, giving precise descriptions of the involved molecules and proteins. Our model is created on the basic principles of finite state machines. It is a biological automaton, that moves from the learning states, to the memorizing and recognizing states, as it was presented in Fig. 1. For a detailed analysis of the underlying finite state machine please see the section Finite State Machine View of the System.

Sensors

As we can observe in Fig. 3, our system is composed from three basic subparts. The first part is the part containing the sensors. Our sensors are the proteins LacI, luxR and TetR, and they are constitutively produce, in order to regulate the operation of the rest of the system. The sensing subsystem can be seen in Fig. 4.

Fig. 4: The proteins that act as sensors are constitutively produced.

Memory

The second subsystem is responsible for the creation and control of memories. The memory control is based on the following underlying mechanisms:

• The sensor proteins form complexes together with the inducers. These complexes are used to either activate (in case of the complex consisting of luxR and AHL) or repress (in case of the complexes consisting of LacI and IPTG as well as TetR and aTc) the DNA transcription of the proteins cI and p22cII.
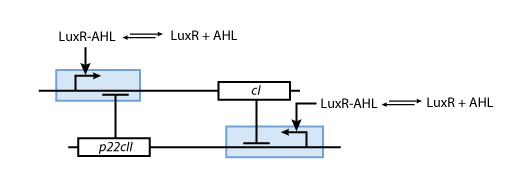
• p22cII and cI repress the DNA transcription of each other, so that the closed loop system behaves as a toggle; a dynamic system with only two possible steady states (see Fig. 6).

Fig. 5: Learning system. Depending on the inputs IPTG or aTc the proteins cI and p22cII are produced.

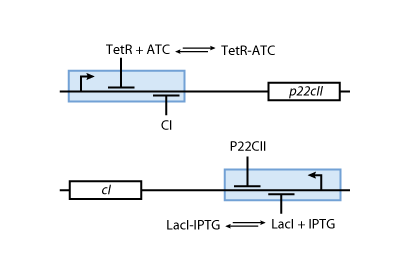
• Fig. 5 shows the protein production system that is used during the learning phase. During the learning phase, there is still no cI or p22cII produced. They are produced, only if either IPTG or aTc is added, respectively. Since no AHL is present, the inner toggle switch (see Figure 6) is turned off.

Fig. 6: Memory system. If AHL is present the production of either cI or p22cII is continued.

• During the memory phase, AHL is added and the IPTG and aTc are removed. That is why only the inner toggle switch (see Fig. 6) is turned on while the protein production systems shown in Fig. 5 are deactivated. Depending on what was produced during the learning phase, the production of either cI or p22cII is continued. That is why the system can act as memory, effectively storing the information that it is exposed to.

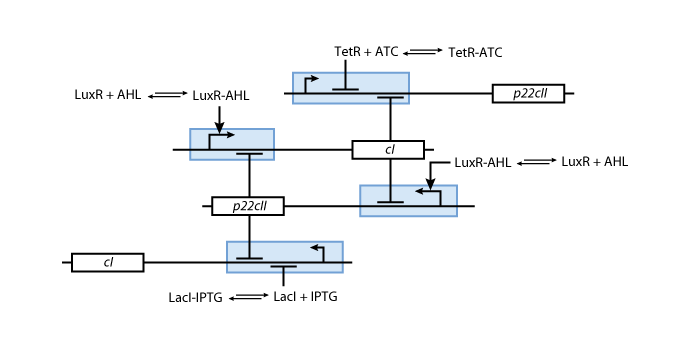
Based on all the above, we present the final assembly of the memory subsystem in Fig. 7.

Fig. 7: Final interaction of the learning and memory system. The memory content is represented by the concentrations of the proteins cI and p22cII.

Reporters

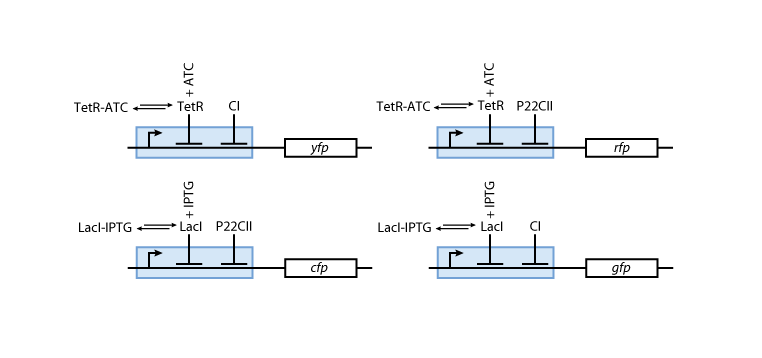
Fig. 8 gives an overview about the reporter subsystem. Florescent reporter proteins are expressed depending on the inducer concentrations, and the concentrations of cI and p22cII. For example, the presence of either TetR or cI will repress the production of YFP. However, if the inducer aTc is present, aTc will bind to TetR which can no longer block the production of YFP. We are using four fluorescent proteins, to encode the steady states of our system at the final recognition stage. This way, we are able to distinguish between all the different transition paths of our biological automaton.

Fig. 8: The production of the florescent reporter proteins depends on the memory content (cI or p22cII) and the current input (aTc or IPTG).

Final Model

We have so far presented all the parts that are needed in order to model and simulate the behavior of a biological automaton with the ability to memorize and recognize the chemical that it is exposed to. By following the details presented in the previous section, we have all the necessary information to fully understand the interior of the black boxes that were presented in Fig. 2 and Fig. 3. Our overall system model is presented in Fig. 9.

Fig. 9: Final model of the EducatETH E. coli system.

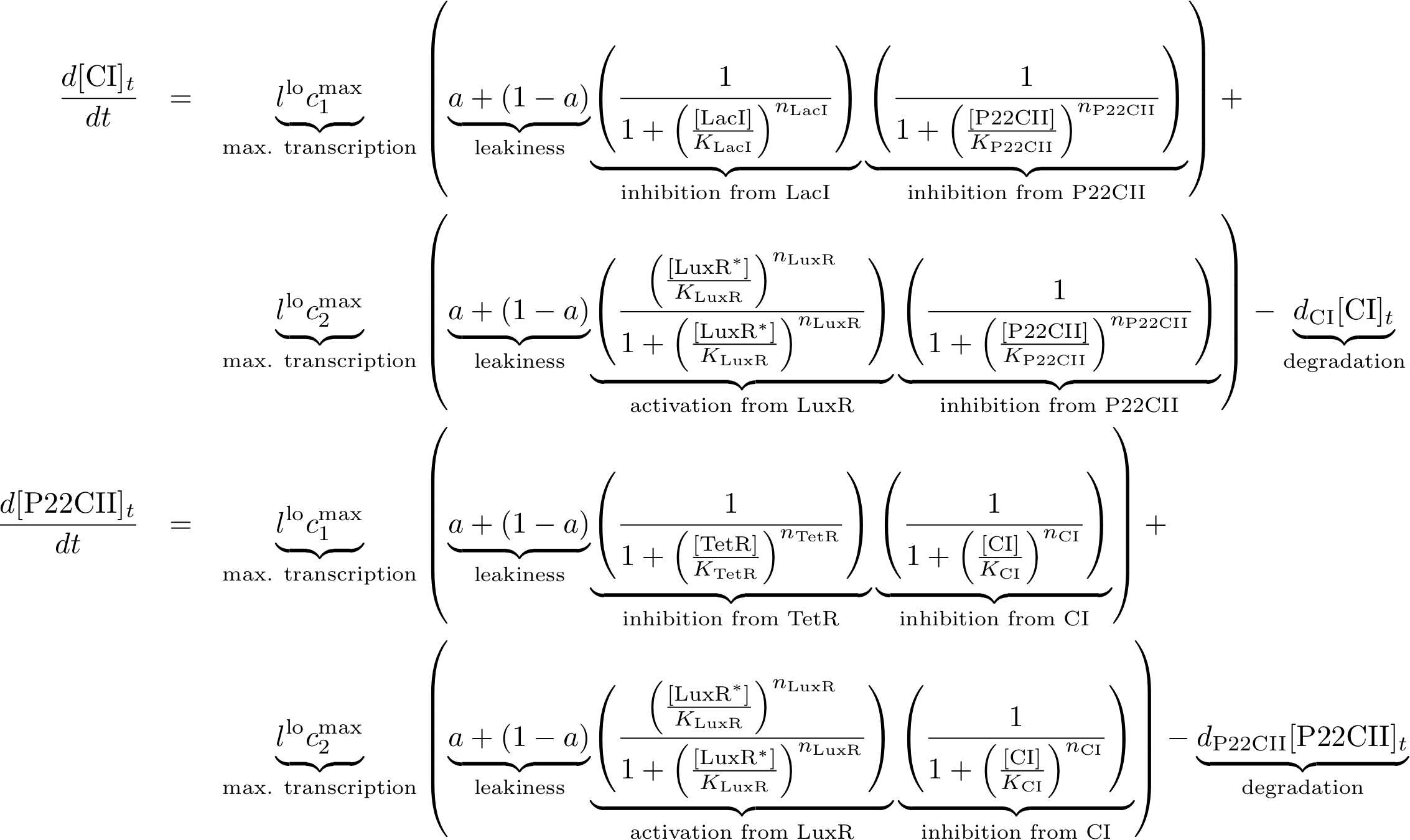
Mathematical Model

Based on the modeling that we have done so far, we can derive the equations that govern the behavior of our system. The model is governed by sets of coupled ordinary differential equations which are presented in the following. We use a simple notation for the different elements of the equations. Namely:

• All concentrations are given in brackets (for example [cI]).
• All decay constants are described by a variable d followed by the name of the protein they refer to.
• The production of the proteins is described by a basic constant production level that models the leak of the production system, and a factor of l and c_max that describe the maximum production of a protein, given in [M].
• Depending on whether the DNA for a protein is implemented on a low or a high copy plasmid, we distinguish between l_lo and l_hi, respectively.

For a more basic introduction into how we transfered our model into equations, see the section Modeling Basics.

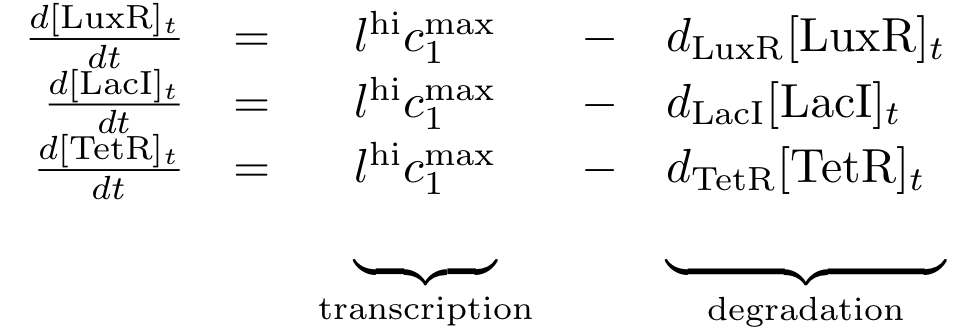
Constitutively produced proteins

The equations for the constitutively produced proteins are very simple, since there is no dependence on other proteins. They are designed so that the protein concentration reaches the value l_hi*c_max/d at steady state.

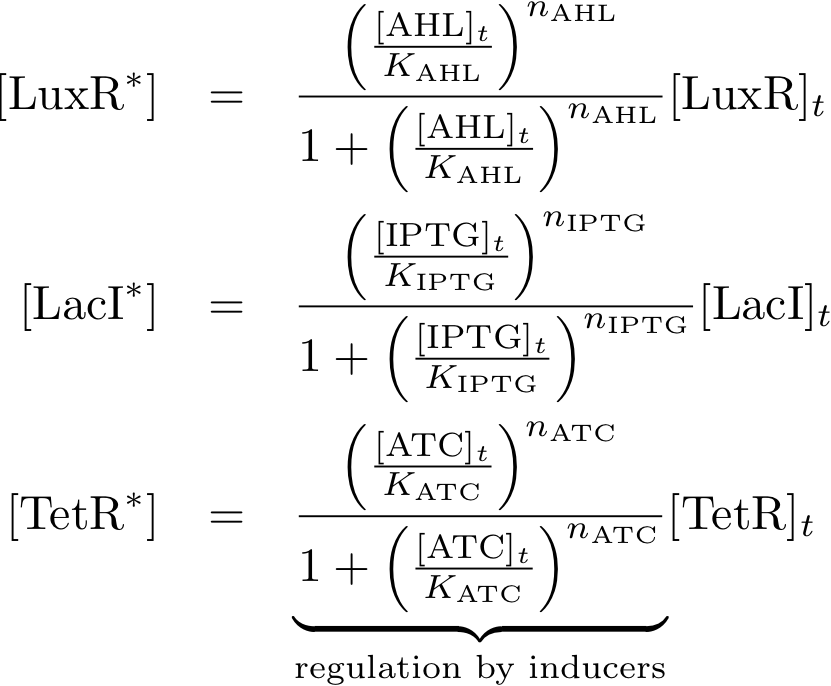
Allosteric regulation

These equations describe the formation of complexes between the inducers and sensor proteins. We do not use differential equations, but we describe directly the concentrations of the complexes. This is a valid assumption, provided that we always wait sufficient time, and the system reached a steady state. We describe the total amount of proteins with the index 't', while we use the index '*' for proteins that build a complex with their respective inducer. For example:

• [TetR_t] describes the total amount of TetR that is available.
• [TetR_*] describes the proteins that are available as a complex with aTc, and
• [TetR] gives the concentration of free TetR proteins.

Learning and memory subsystem

The learning and memory subsystem is the core of the system that we are trying to model and implement. It is characterized by the feedback between its state variables/proteins cI and p22cII. Its behavior is further complicated by the variation of the production of the aforementioned proteins because of the inputs. The following equation describe the concentrations of the memory proteins as a system of coupled differential equations. The equations consist of two major production parts and a decay part.

• The first production part models the production of either cI or p22cII during the learning phase, and corresponds to the model in Fig. 5.
• The second production part describes the inner toggle switch that was shown in Fig. 6.

Reporting subsystem

The equations for the reporting subsystem finally describe the production of the florescence proteins depending on the inputs and memory proteins as modeled in Figure 8. Note that both inputs and memory proteins act repressively on the production of the florescence proteins. So e.g. YFP is only produced when there is both no cI and all TetR is bind in a complex together with aTc.

The systems of equations that we have presented, describe and predict the behavior of our system. We have simulated the behavior of our system at steady states, and the results can be seen in the section Simulations. In order to increase the accuracy of our results, we have conducted an extensive literature survey, in order to isolate and find the parameters of our system. Since this is a burden for every team undertaking a complicated project in synthetic biology, we are presenting our full table of parameters in the Parameters page.</html>