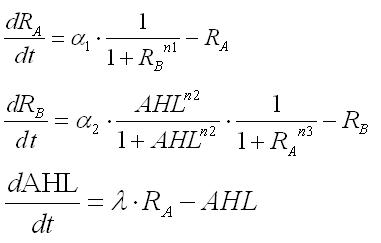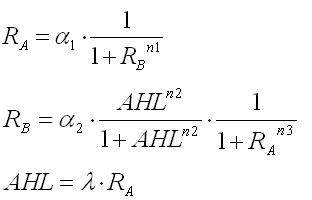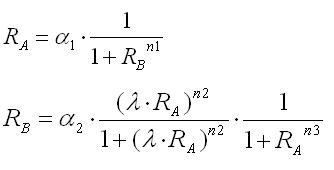Tokyo/Formulation/3.AHL-experssing model
From 2007.igem.org
(Difference between revisions)
| Line 1: | Line 1: | ||
<br>大腸菌の中からAHLを産生している系を考えてみる.すると,微分方程式がもう一本増え3連立の微分方程式になる. | <br>大腸菌の中からAHLを産生している系を考えてみる.すると,微分方程式がもう一本増え3連立の微分方程式になる. | ||
| + | Taking into consideration the system with AHL produced by E. coli themselves, it is necessary to add another differential equation; therefore, the whole system is expressed by three simultaneous equations. | ||
<br> [[Image:expression3-4.jpg|400px|]][[Image:parameter3-1.jpg|200px|]] | <br> [[Image:expression3-4.jpg|400px|]][[Image:parameter3-1.jpg|200px|]] | ||
| Line 8: | Line 9: | ||
<br>定常状態では, | <br>定常状態では, | ||
| - | + | In the steady state, | |
<br>[[Image:expression3-2.jpg|300px|]] | <br>[[Image:expression3-2.jpg|300px|]] | ||
<br>となる.すると,3本目の式を2本目の式に代入することができ,結局RaとRbの2変数になる.これより,今までと同様RaとRbの相平面が描ける. | <br>となる.すると,3本目の式を2本目の式に代入することができ,結局RaとRbの2変数になる.これより,今までと同様RaとRbの相平面が描ける. | ||
| + | The third equation is now substituted into the second. Now the variants being two, Ra and Rb, it is possible to draw the same type of phaseplane of Ra and Rb. | ||
<br>[[Image:expression3-3.jpg|300px|]] | <br>[[Image:expression3-3.jpg|300px|]] | ||
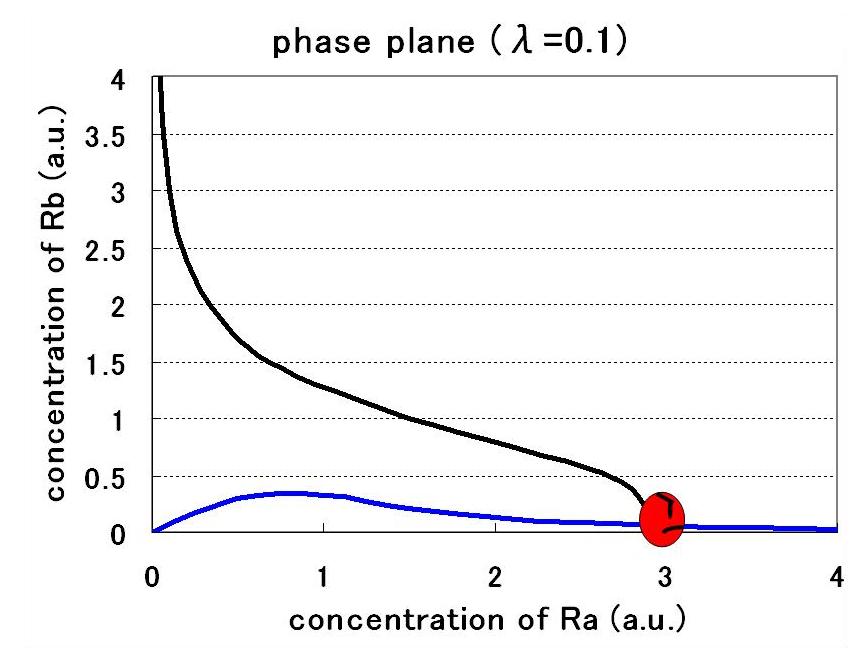
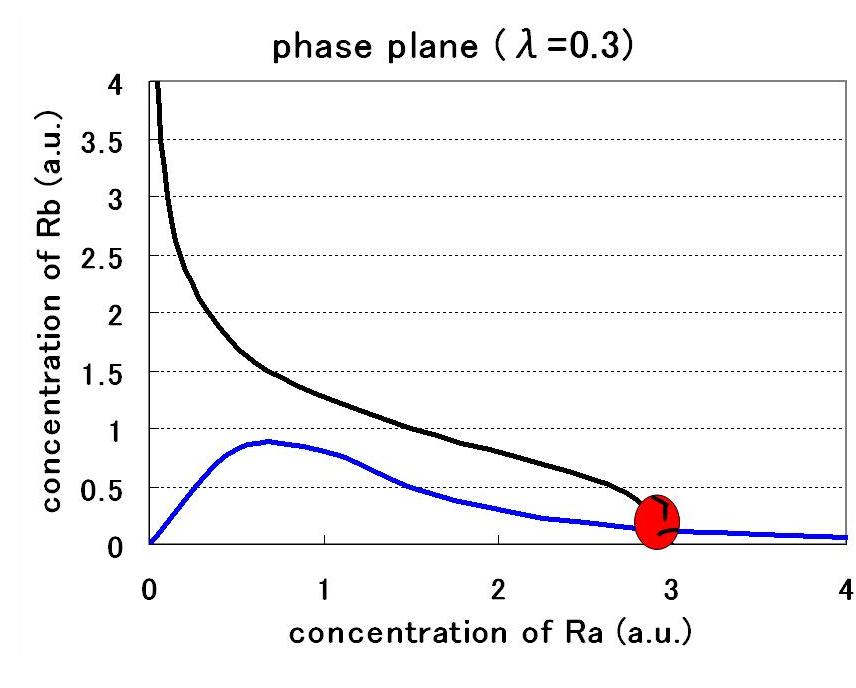
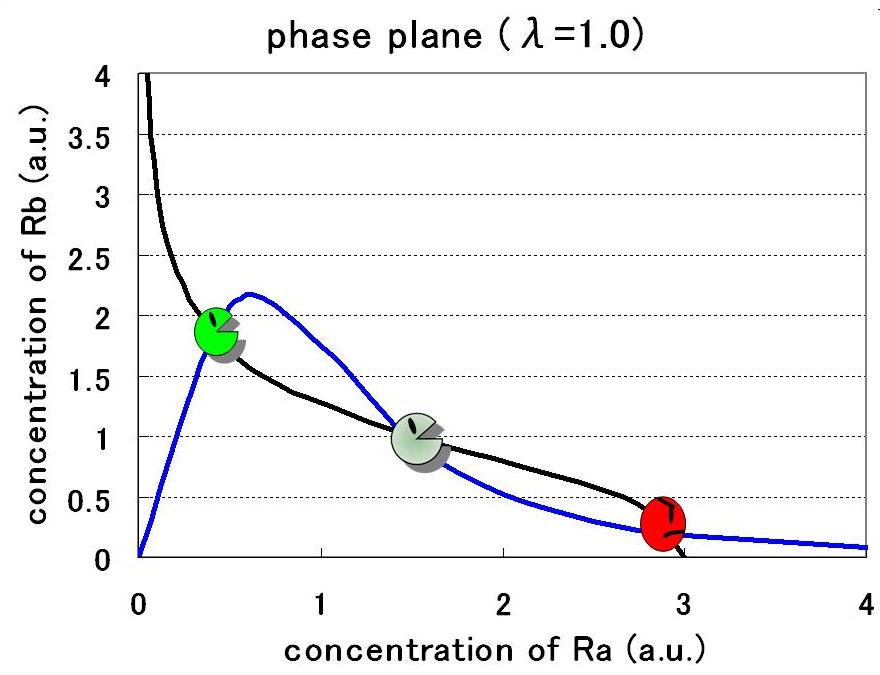
<br>今回も,パラメータの選び方により,安定点が一つのときと二つのときが出てくる. | <br>今回も,パラメータの選び方により,安定点が一つのときと二つのときが出てくる. | ||
| + | In this case as well, the parameter choice can result in one or two equibrium points. | ||
<br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]] | <br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]] | ||
Revision as of 04:05, 22 October 2007
大腸菌の中からAHLを産生している系を考えてみる.すると,微分方程式がもう一本増え3連立の微分方程式になる.
Taking into consideration the system with AHL produced by E. coli themselves, it is necessary to add another differential equation; therefore, the whole system is expressed by three simultaneous equations.
demenionless にすると,
定常状態では,
In the steady state,
となる.すると,3本目の式を2本目の式に代入することができ,結局RaとRbの2変数になる.これより,今までと同様RaとRbの相平面が描ける.
The third equation is now substituted into the second. Now the variants being two, Ra and Rb, it is possible to draw the same type of phaseplane of Ra and Rb.
今回も,パラメータの選び方により,安定点が一つのときと二つのときが出てくる.
In this case as well, the parameter choice can result in one or two equibrium points.