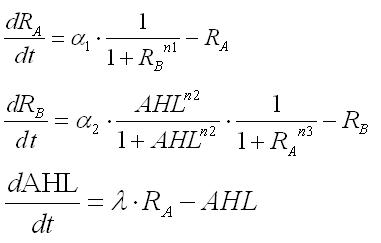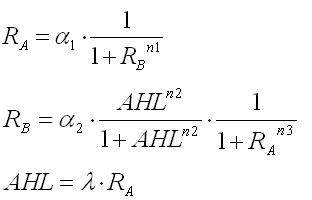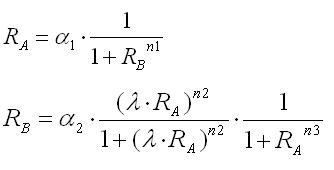From 2007.igem.org

Works top   0.Hybrid promoter   1.Formulation   2.Assay1   3.Simulation   4.Assay2   5.Future works

Step1   Step2   Step3　　

Step.3 Single cell model with hybrid promoter and cell-produced AHL

The differential equations of the system considering AHL produced by E.coli themselves were given as

These equations were normalized as follows:

In the steady state,time derivatives are zero.As a result,the nullclines of this system were derived as

By substituting the third equation into the second,the nullclines for Ra and Rb were obtained as

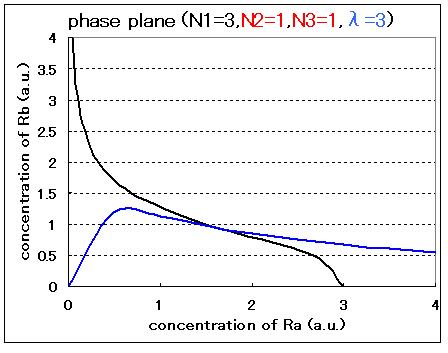
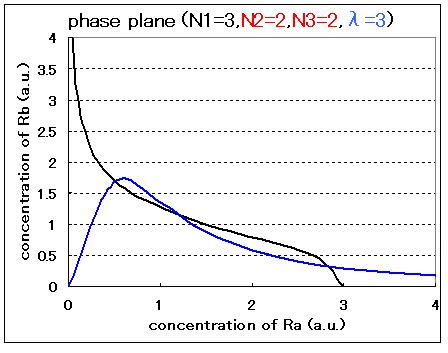
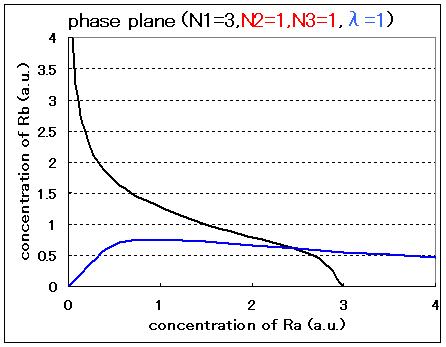
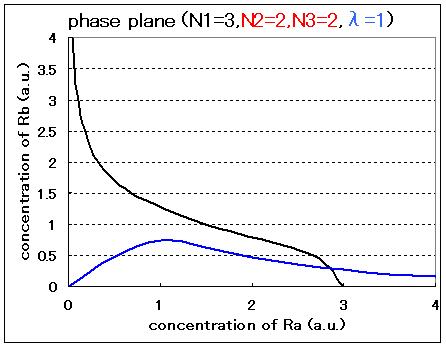
Therefore, the phase plane of this system can be plotted as Fig.3.1.A-D and the number of equilibrium points were decided by the value of the parameters:

Comparison between Fig3.1.A and B indicated that Hill coefficients are critical parameters even in the cell-produced AHL model. In the case of N2=1, N3=1, and λ=3, the phase plane was monostable. In contrast, in the case of N2=2, N3=2, and λ=3, the phase plane was bistable.
In the cases of λ=1 (Fig.3.1.C and D), the system can not take bistability even if the values of Hill coefficients are changed. For the implementation of the circuit in a cell, the parameter λ should be controlled by changing the RBSs and/or promoter sequences of LuxR.

Step.3 >> Formulation top