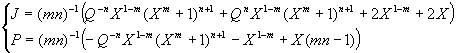Saint Petersburg/AlgebraJP
From 2007.igem.org
< Saint Petersburg(Difference between revisions)
m (→Bistable behaviour of two repressors, mutually repressing each other) |
|||
| Line 1: | Line 1: | ||
==Bistable behaviour of two repressors, mutually repressing each other== | ==Bistable behaviour of two repressors, mutually repressing each other== | ||
| - | [[Saint_Petersburg|Main page]] [[Saint_Petersburg/Algebra|Back to | + | [[Saint_Petersburg|Main page]] |
| + | |||
| + | [[Saint_Petersburg/Algebra|Back to Algebra page]] | ||
Bifurcation set in (''J'', ''P'') cross section is given by the following parametric equations: | Bifurcation set in (''J'', ''P'') cross section is given by the following parametric equations: | ||
| - | + | [[Image:spb_eqn_028.gif]] | |
| - | + | ||
| - | + | ||
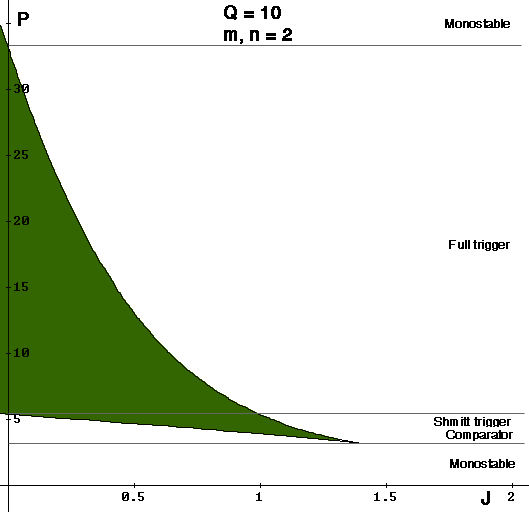
| + | To obtain the bifurcation curve one should plot the second parameter versus the first, varying ''X'' from 0 to ''P+J''. The cusp is located as shown in the figure below. While Q is increasing the cusp tip moves right and upwards. | ||
| + | |||
| + | [[Image:bifurc_JP1.gif]] | ||
Important findings: | Important findings: | ||
| - | At constant value of Q and increasing values of P the behaviour changes in the following way: | + | At constant value of ''Q'' and increasing values of P the behaviour changes in the following way: |
*Small ''P'' – monostable behaviour | *Small ''P'' – monostable behaviour | ||
| Line 24: | Line 27: | ||
See also: | See also: | ||
| - | [[Saint_Petersburg/Algebra|(''P,''Q'')-Cross Section]] | + | [[Saint_Petersburg/Algebra#The results|(''P,''Q'')-Cross Section]] - analysis of hysteresis existense |
| - | [[Saint_Petersburg/AlgebraJQ|(''J,''Q'')-Cross Section]] | + | [[Saint_Petersburg/AlgebraJQ|(''J,''Q'')-Cross Section]] - type of responce at various values of ''Q'' |
Latest revision as of 08:53, 22 October 2007
Bistable behaviour of two repressors, mutually repressing each other
Bifurcation set in (J, P) cross section is given by the following parametric equations:
To obtain the bifurcation curve one should plot the second parameter versus the first, varying X from 0 to P+J. The cusp is located as shown in the figure below. While Q is increasing the cusp tip moves right and upwards.
Important findings:
At constant value of Q and increasing values of P the behaviour changes in the following way:
- Small P – monostable behaviour
- Intermediate P – Shmitt trigger/comparator
- Large P – true trigger (sensitivity increase as P increase)
- Very large P – monostable behaviour
See also:
(P,Q)-Cross Section - analysis of hysteresis existense
(J,Q)-Cross Section - type of responce at various values of Q