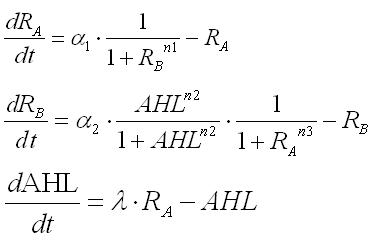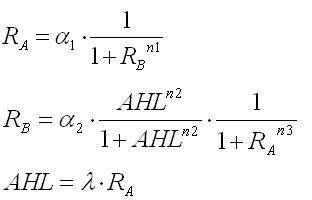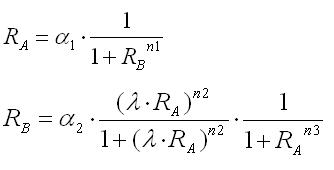Tokyo/Formulation/3.AHL-experssing model

From 2007.igem.org

(Difference between revisions)
Line 1: Line 1:
-
<br>大腸菌の中からAHLを産生している系を考えてみる．すると，微分方程式がもう一本増え3連立の微分方程式になる．
+
<br>The differential equaitons of the system considering AHL produced by E.coli themselves were given as
-
Taking into consideration the system with AHL produced by E. coli themselves, it is necessary to add another differential equation; therefore, the whole system is expressed by three simultaneous equations.
+
<br> [[Image:expression3-4.jpg|400px|]][[Image:parameter3-1.jpg|200px|]]
<br> [[Image:expression3-4.jpg|400px|]][[Image:parameter3-1.jpg|200px|]]
-
<br>demenionless にすると，
+
<br>These equations were normalized as follows:
<br>[[Image:expression3-1.jpg|300px|]]
<br>[[Image:expression3-1.jpg|300px|]]
-
<br>定常状態では，
+
<br>As a result,the nullclines of this system were derived as
-
In the steady state,
+
<br>[[Image:expression3-2.jpg|300px|]]
<br>[[Image:expression3-2.jpg|300px|]]
-
<br>となる．すると，3本目の式を2本目の式に代入することができ，結局RaとRbの2変数になる．これより，今までと同様RaとRbの相平面が描ける．
+
<br>By substituting the third equation into the second,the nullclines for Ra and Rb were obtained as
-
The third equation is substituted into the second. Now the variants being two, Ra and Rb, it is possible to draw the same type of phaseplane of Ra and Rb.
+
<br>[[Image:expression3-3.jpg|300px|]]
<br>[[Image:expression3-3.jpg|300px|]]
-
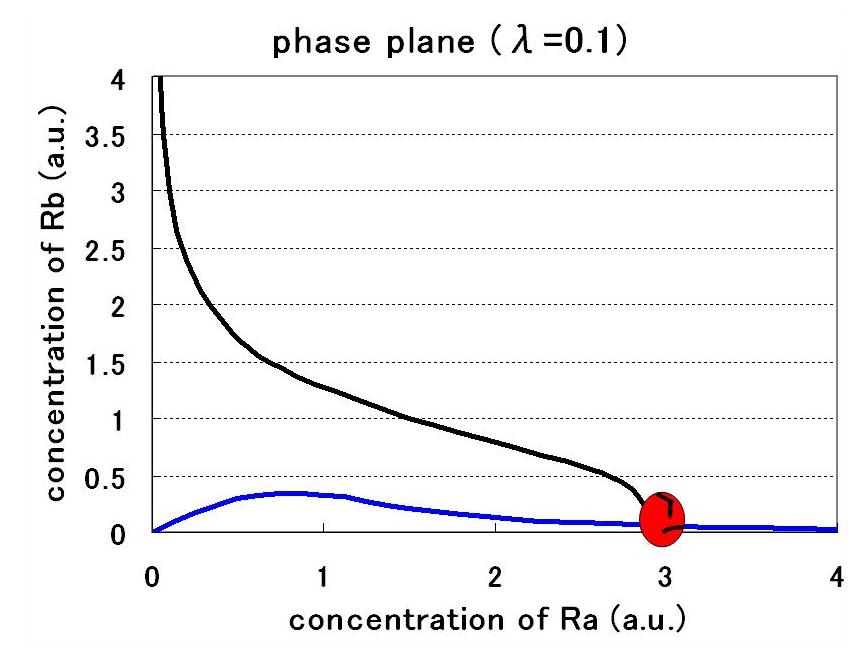
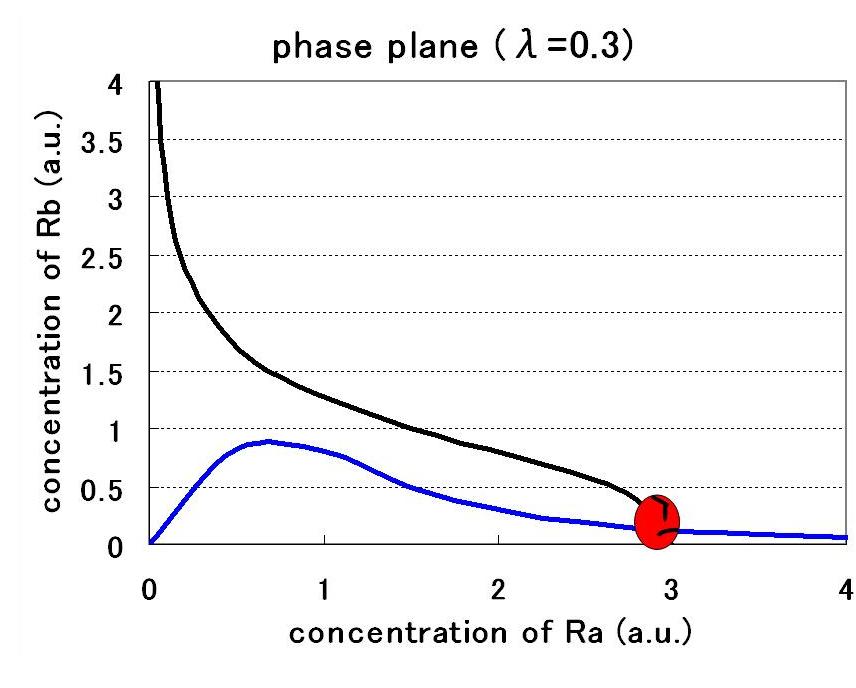
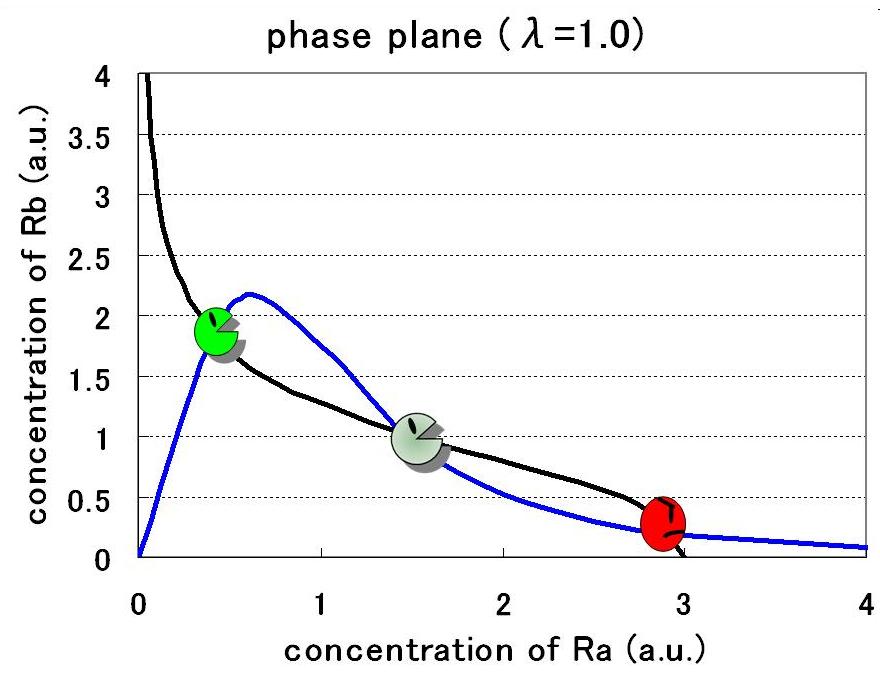
<br>今回も，パラメータの選び方により，安定点が一つのときと二つのときが出てくる．
+
<br>Therefore, the phase plane of this system can be plotted as Fig● and the number of equilibrium points were decided by the value of the parameters:
-
In this case as well, the parameter choice can result in one or two equibrium points.
+
<br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]]
<br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]]

Revision as of 13:31, 23 October 2007


The differential equaitons of the system considering AHL produced by E.coli themselves were given as


Expression3-4.jpgParameter3-1.jpg


These equations were normalized as follows:


Expression3-1.jpg


As a result,the nullclines of this system were derived as


Expression3-2.jpg


By substituting the third equation into the second,the nullclines for Ra and Rb were obtained as


Expression3-3.jpg


Therefore, the phase plane of this system can be plotted as Fig● and the number of equilibrium points were decided by the value of the parameters:


Phaseplane3-1.jpg Phaseplane3-2.jpg Phaseplane3-3.jpg

Retrieved from "http://2007.igem.org/wiki/index.php/Tokyo/Formulation/3.AHL-experssing_model"