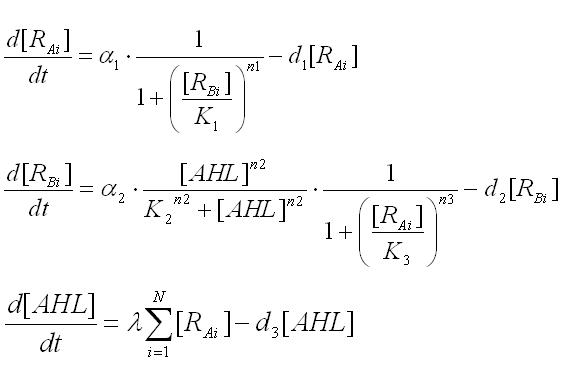Tokyo/Works/Simulation
From 2007.igem.org
| Line 3: | Line 3: | ||
<!--==ここまでわかったこと==--> | <!--==ここまでわかったこと==--> | ||
| + | ==シミュレーションはpopulationモデルに拡張し,確率微分方程式を用いた == | ||
| + | |||
| + | <!-- | ||
| + | Here the concentration of AHL outside of the cells was assumed to be the same concentration of AHL inside the cell according to the description that AHL is freely permiable through cell membrane in the referenced articles.The phase plane analysis was made possible by focusing on an indivisual cell.The parameter N was assumed to be the number of the cells. | ||
| + | |||
| + | However, all the individuals behaved in the same way in this deterministic model. To see the bahavior of each individual cell, it is necessary to carry out stocastic simulation. | ||
| + | '''[[Tokyo/Formulation/4.population model| ⇒ see more]]''' | ||
| + | --> | ||
| + | |||
| + | [[Image:expression4-1.jpg|300px|thumb|none|Ex3.1 the differential equations of population model]] | ||
| + | |||
| + | <!-- | ||
| + | we introduced the differential equations of step4 into Poisson random variables to simulate the stochastic model. | ||
| + | <br>By using simulation with stochastic model, every cell can take different behavior. | ||
| + | --> | ||
| + | |||
| + | <br>[[Image:expression5-1.jpg|400px|thumb|none|Ex3.2 the stochastic differential equations of the population model]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
== What we have found so far == | == What we have found so far == | ||
Revision as of 15:17, 26 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
シミュレーションはpopulationモデルに拡張し,確率微分方程式を用いた
What we have found so far
Wet experiments have determined Hill coefficients, coefficients of repression and activation of AHL and LacI(n2,n3,k2,k3) as follows.
n2 = 2.08 (-)
K2 = 4.05 (μM)
n3 = 2.47 (-)
K3 = 0.295 (μM)
Determining the range of parameter which satisfy coexistent stability
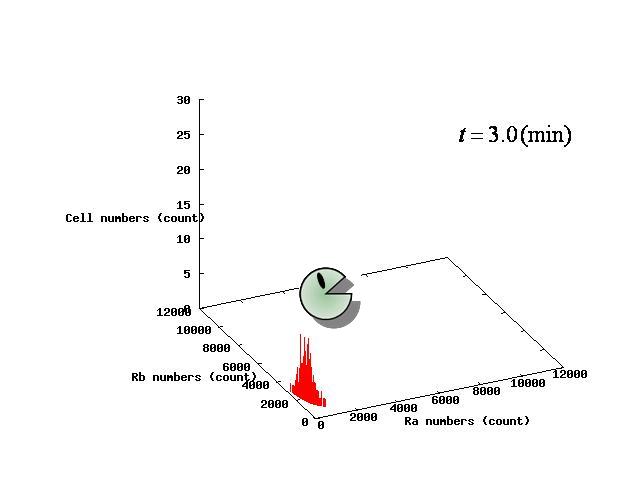
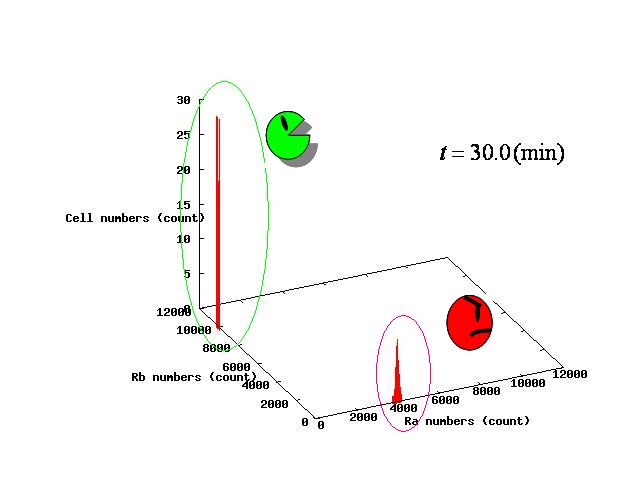
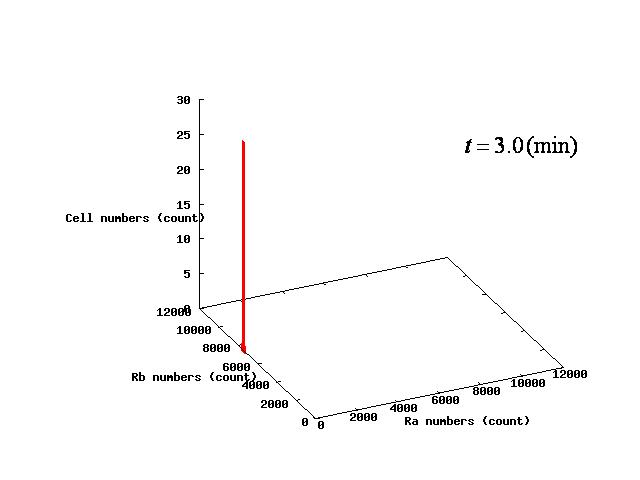
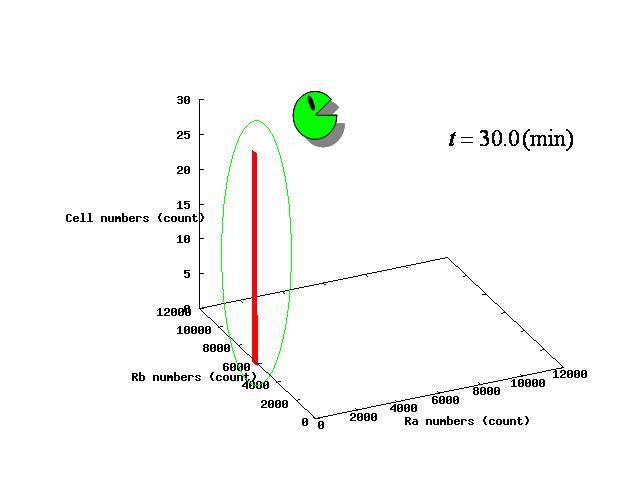
The example of coexistent stable state
⇒ movie here!!
⇒ movie here!!
⇒ movie here!!
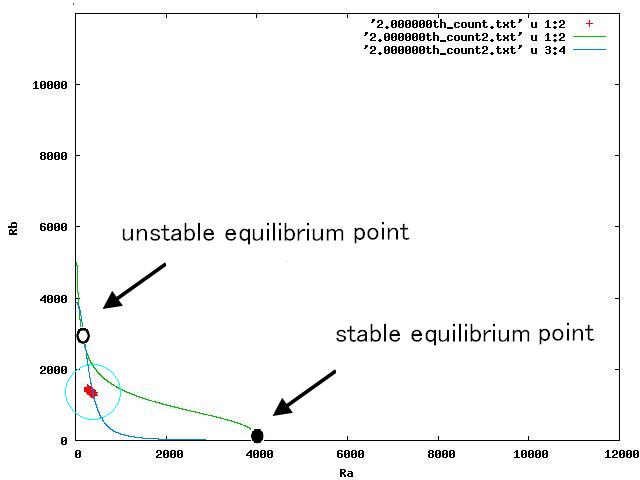
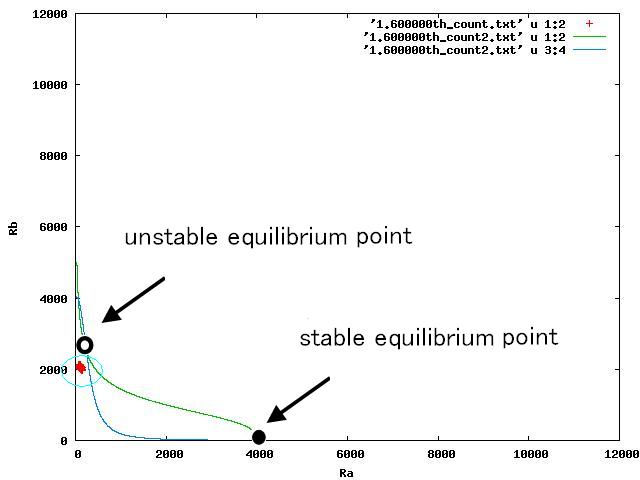
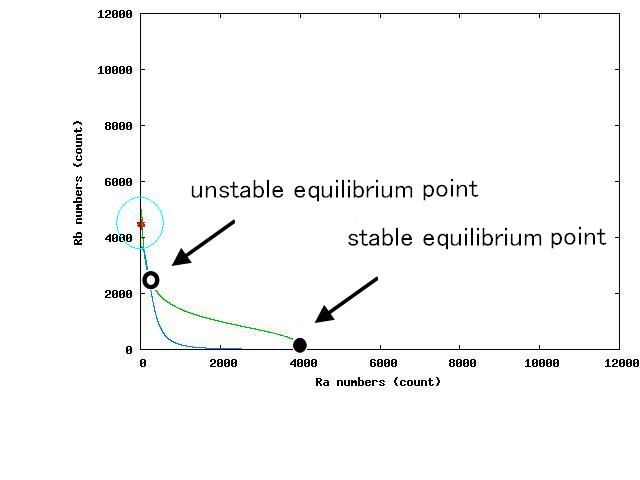
For the three patterns, the phase portraits at the moment when the number of the intersection of nullclines become two are shown in Fig.4.A-C respectively.
Fig.4.A shows that when the two equilibrium points appeared, cells were existing closer to A-side than the unstable equilibrium point. Oppositely,in Fig.4.C,when the two equilibrium points appeared, cells were existing closer to A-side than the unstable equiliblium point. Since when the number of the intersection of nullclines becomes two, stable point appears on B-side, at the moment of Fig.4, cells on the A-side cannot transit to B-side across unstble equilibrium point. As a result, all cells transit to A-side.
⇒ movie about Fig.4.A here!!
⇒ movie about Fig.4.B here!!
⇒ movie about Fig.4.C here!!
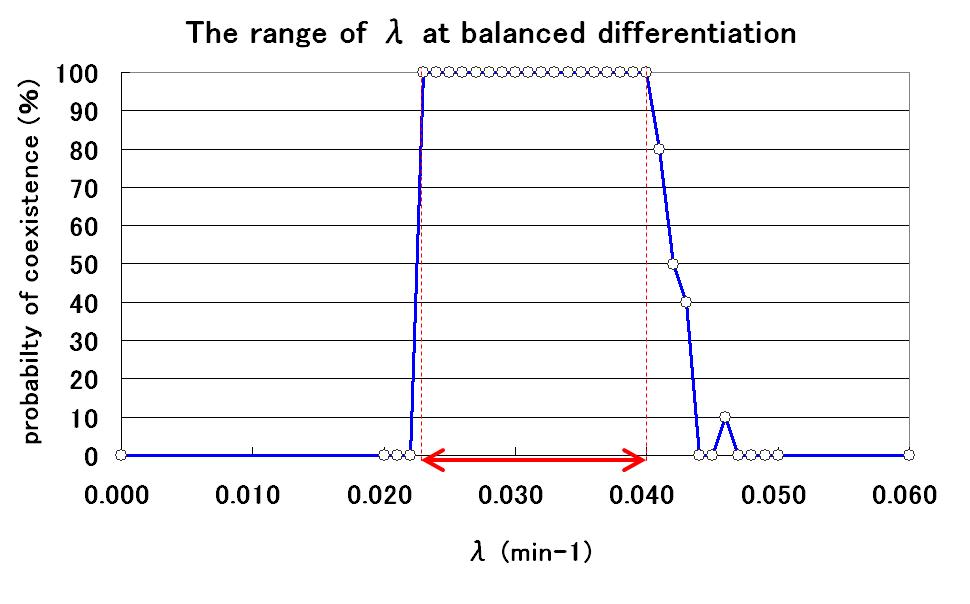
The range of parameter λ
To determine the range of parameter λ, several simulations were conducted with different values of λ. As a result, the relationship between λ value and the probability of coexistence is determined as shown in Fig.5.
By using parameter λ in this range, we can construct our model.