Tokyo/Model
From 2007.igem.org
(Difference between revisions)
(→E.coli Follows Pareto's principle!) |
|||
| Line 10: | Line 10: | ||
'''Bistable state ⇒ The removal of A (worker) ⇒ Unstable state with only B left ⇒ Regain of "stable coexistence"''' | '''Bistable state ⇒ The removal of A (worker) ⇒ Unstable state with only B left ⇒ Regain of "stable coexistence"''' | ||
<br><br> | <br><br> | ||
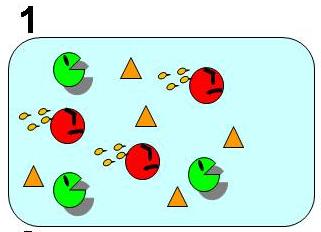
| - | [[Image: | + | [[Image:1state.JPG|thumb|190px|'''Fig. 1 Condition 1. Bistable state''' <br>The system is stable when it contains both A (worker) and B (idler) at certain ratio.|left]] |
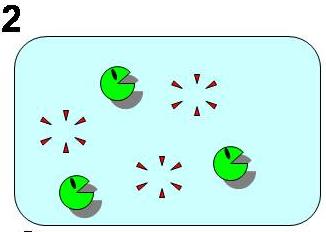
| - | [[Image: | + | [[Image:2state.JPG|thumb|190px|'''Fig. 2 Condition 2. Removal of A''' <br>Now that A (worker) is removed, there is only B (idler) left.|center|left]] |
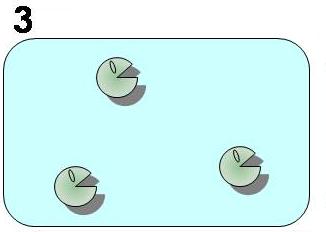
| - | [[Image: | + | [[Image:3state.JPG|thumb|190px|'''Fig. 3 Condition 3. Unstable B''' <br>While after the removal of A (worker), B becomes unstable and "stable coexistence" of the system is broken.|center|left]] |
<!--Node B detects the removal of node A from the system and knows that there is only node B left.--> | <!--Node B detects the removal of node A from the system and knows that there is only node B left.--> | ||
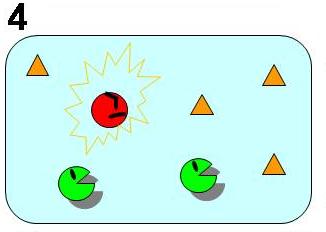
| - | [[Image: | + | [[Image:4state.JPG|thumb|190px|'''Fig. 4 Condition 4. Regain of "stable coexistence"''' <br>Some B (idler) changes to A (worker) while the others remain B (idler). Then the system regains "stable coexistence".|center|left]] |
<br> | <br> | ||
<!--[[Image:concepts.jpg]]--> | <!--[[Image:concepts.jpg]]--> | ||
Revision as of 17:13, 26 October 2007
Abstract Concept & Model Requirements Genetic_circuit Works About_our_team
E.coli Follows Pareto's principle!
To follow Pareto’s principle like an ant society, our model system must satisfy the three conditions shown in Fig. 1 to 4. In our model, all individual cells have the same genetic circuits but take either of state A (worker) or B (idler) depending on the surrounding circumstances. ([http://en.wikipedia.org/wiki/Pareto_principle What is Pareto's principle? (Wikipedia)])
As shown in Fig. 1, 2, 3, and 4, the condition of the system is changing as follows:
Bistable state ⇒ The removal of A (worker) ⇒ Unstable state with only B left ⇒ Regain of "stable coexistence"